由贝特朗概率悖论得到的一个有趣现象
●
(温州华侨职业中等专业学校 浙江温州 325000)
由贝特朗概率悖论得到的一个有趣现象
●徐新
(温州华侨职业中等专业学校 浙江温州 325000)
文章通过对贝特朗概率悖论分析,发现这样的概率模型,其样本空间可以是一维直线的区间,也可以是二维平面的区域.究其原因,是因为随机变量函数具有特殊的性质,构造出类似的随机变量函数,可以得到类似的概率模型.
贝特朗概率悖论;几何概型;随机事件;样本空间
贝特朗概率悖论(下文简称悖论)由贝特朗于1889年提出,它说明这样一个原理:解决一个实际问题的时候,必须建立无歧义的概率模型[1].事实上,因为该悖论对问题的表述含糊,从而造成理解上的歧义,所以其本身并不能直接求解.为此,我们必须先将其含糊的表述加以明确,得到确定的随机试验,从而建立无歧义的概率模型,再对相应的概率模型进行求解.
通常对“在圆内任作一弦”进行明确,可得到多种不同的随机实验[2].笔者讨论以下两种情况的概率模型:1)弦的两个端点都是在圆周上随机地取;2)弦的一个端点固定在圆周上,另外一个端点在圆周上随机地取.

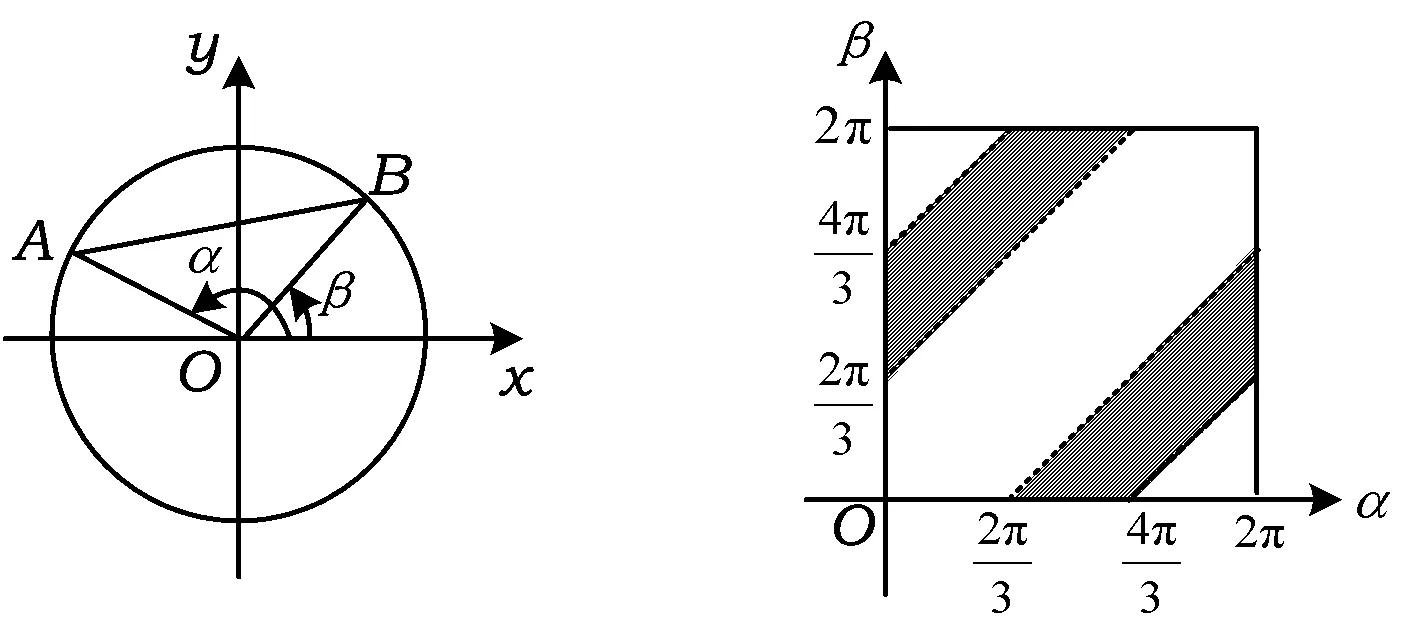
图1 图2
解如图1所示,依据圆的参数方程,设A(cosα,sinα),B(cosβ,sinβ),其中α,β∈[0,2π],从而样本空间为[0,2π]×[0,2π].由题意,
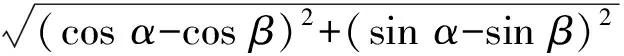
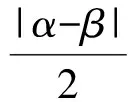
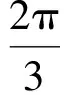
对应区域是图2中的阴影部分.由几何概型的定义,得
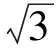

解法1依据圆的参数方程,设A(cosα0,sinα0),B(cosβ,sinβ),α0是区间[0,2π]上取定的值.由点B的随机性,知β∈[0,2π],因此样本空间是[0,2π].此时,
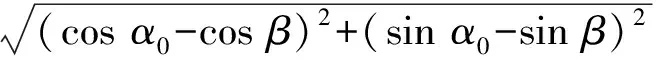
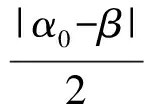
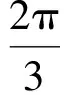
下面根据β的取值范围求解:
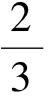
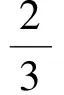

图3 图4 图5
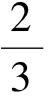
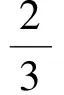

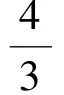
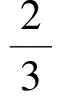
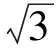
模型2的解法1与模型1的解法形成比较,表述较为复杂,下面给出模型2的简洁解法.
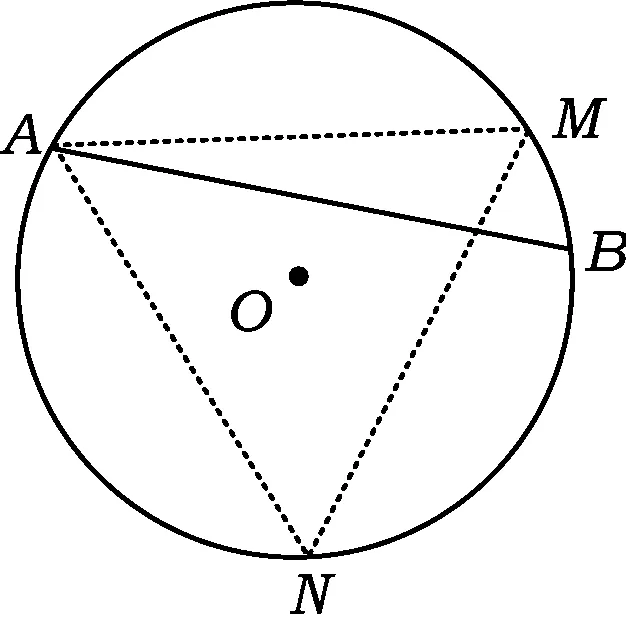
图6

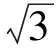

在模型1的解法中,记
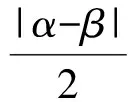
η=f(α,β)是随机变量,α,β是[0,2π]上均匀分布的随机变量.类似模型1的求解,可求得其概率分布函数
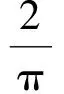
在模型2的解法中,记
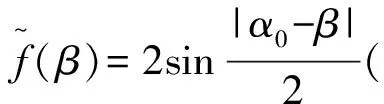
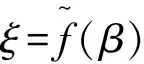
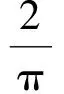
不难看出,上述两个概率分布函数是同一个函数.
因此,如果在悖论中将“在圆内任作一弦”明确为“在圆周上取两点任作一弦”,就可以得到确定的概率模型,即下面的模型3.

模型3有两种解法:1)参照模型1的解;2)参照模型2的解.如果把悖论中“在圆内任作一弦”错误地理解为“在圆周上取两点任作一弦”,那么就会认为该悖论有解.这就使悖论更具迷惑性.
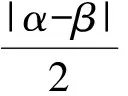
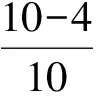
值得注意的是:所得概率值相同,并不意味着概率模型一定可以放到两个不同维数的样本空间上.
模型4甲和乙两人相约在上午8~9点之间在某地见面,问甲、乙到达某地的时间差的绝对值落在区间(20,40)上的概率.
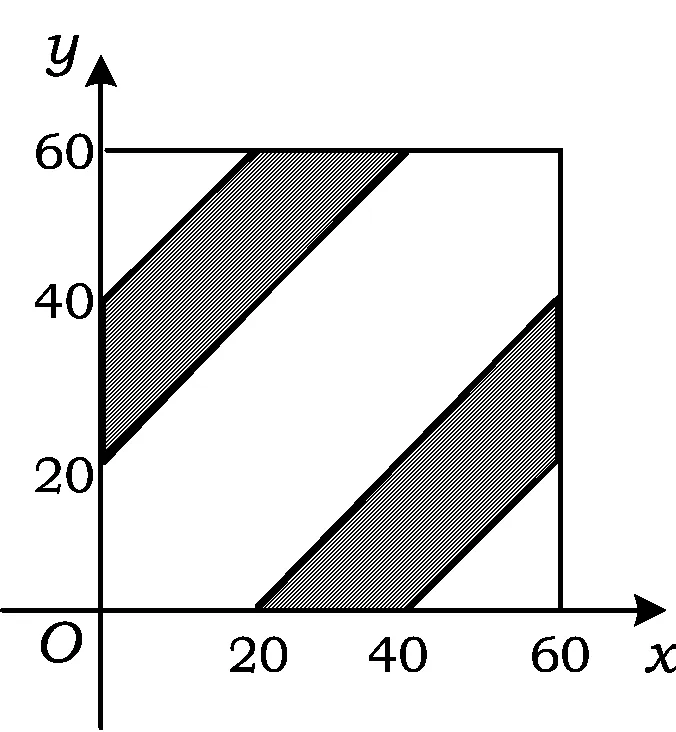
图7
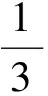
如果在区间[0,60]上任意取定一个值x0,y依然是[0,60]上的均匀随机变量,则得到下面的模型4′.
模型4′ 甲和乙两人相约在上午8~9点之间在某地见面,现已知甲在x0时刻到达了某地,问甲、乙到达某地的时间差的绝对值落在区间(20,40)上的概率.
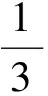
事实上,在上述模型4中,只要甲、乙到达某地的时间差的绝对值所在区间关于30对称,那么相应的随机事件在模型4和模型4′中,计算所得的概率值相等.如果时间差的绝对值所在的区间不关于30对称,比如(10,40),那么相应的随机事件在模型4和模型4′中,计算所得的概率值就不会相等.在模型4中,令z=|x-y|(其中x,y∈[0,60]),那么可得到其概率分布函数是
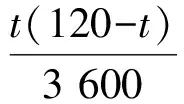
在模型4′中,令
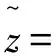
x0是[0,60]上取定的一个值,则可得到其概率分布函数是
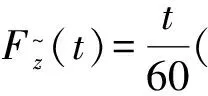
显然,这两者的概率分布函数不是同一个函数.因此,尽管计算所得的概率值相同,但模型4的样本空间只能是区域[0,60]×[0,60],模型4′的样本空间只能是区间[0,60].
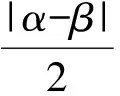
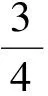
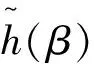
两个模型中的概率分布函数是
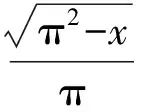
同样,在离散的情况下也有类似现象.
模型6将一枚色子投掷两次,记第一次得到的点数为α,第二次得到的点数为β,求g(α,β)=-||α-β|-3|+3的值大于1的概率.
样本空间是我们所熟知的36个数对构成的集合,对应的概率分布列如表1所示.
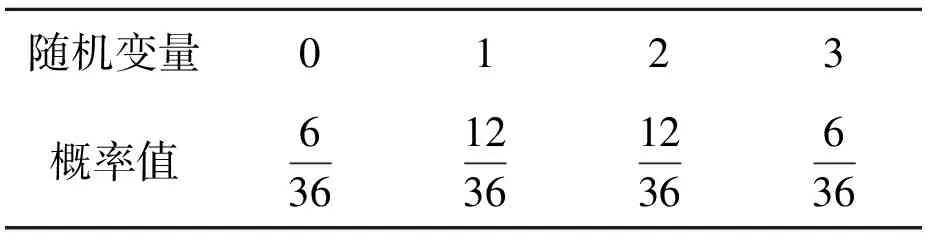
表1 36个数对构成的样本空间所对应的概率分布列
(注:这里的分式没化成最简分式,是为了与下面的分布列作比较.)
2017-04-09;
2017-05-10
徐 新(1979-)男,江西鄱阳人,中学一级教师.研究方向:数学教育.
O122
:A
:1003-6407(2017)07-24-04

