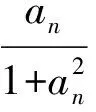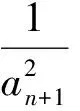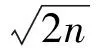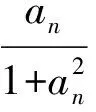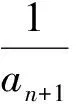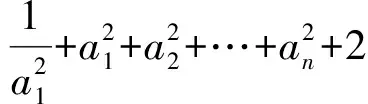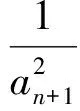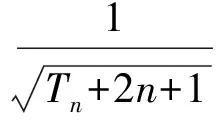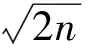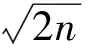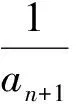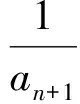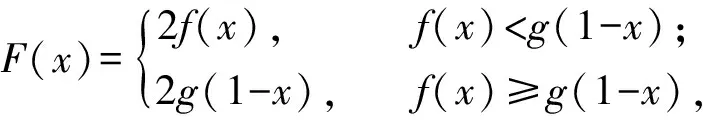浙江试题 八方关注
●
(湖州中学 浙江湖州 313000)
浙江试题八方关注
●冯寅
(湖州中学 浙江湖州 313000)
浙江省高考数学自主命题已有14年,这14年积累了丰富的数学试题,出现了一批新颖的好题.这些题目都是高中数学教学的好素材,整理和分析这些题目可以帮助我们进一步了解高考,有针对性地教学与复习.
数学高考题;关注;问题本质
2004年至今,浙江省数学高考自主命题已经历了 14年.在这14年中,浙江省数学高考试题得到了多方的关注,试题本身也关注了高中数学教学的许多方面:从知识到方法、从思维到能力、从热点到冷点、从概念与理解到思考与角度等[1].笔者将从8个方面谈谈浙江省数学高考试题的特点.
1 关注概念与理解
数学概念就是数学的本质,它是学习数学的基础.解决数学问题应该从正确理解概念出发,抓住概念的本质,这样才能帮助我们更好地制定解题策略.
例1存在函数f(x)满足:对于任意x∈R,都有
( ) A.f(sin 2x)=sinxB.f(sin 2x)=x2+x
C.f(x2+1)=|x+1| D.f(x2+2x)=|x+1|
分析该问题的核心是函数的概念.是否存在函数f(x)满足条件,就是从函数的定义出发,关注定义“对任意的x,有唯一的y与它对应”.此类问题常利用代换的方法来研究,不妨以选项C为例进行说明[2].
选项C的分析:设x2+1=t,则
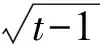
从而f(x2+1)=|x+1|可转化为
对任意的t,f(t)不唯一,因此,这样的函数f(x)不存在.
那么,上面哪个选项通过代换能做到任意唯一呢?
同理分析选项D:设x2+2x=t,则
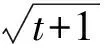
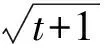
分析4个选项可以知道,除了选项D,其他3个选项作t的代换后都不能得到“对任意的t,有唯一确定的x”.选项D中的函数可以做到“对任意的t,f(t)唯一”,符合函数的定义.
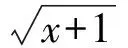
2 关注思考与角度
数学的问题千变万化,不同的理解和认识会得出不同的解决方案.因此,在教学中要善于观察、善于思考,这样才能帮助我们找到合理的途径来解决问题、拓宽思路,培养分析问题和解决问题的能力.
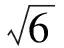
分析此题对|a·e|+|b·e|的理解是关键.从不同的角度来理解|a·e|+|b·e|,可以产生不同的解题策略.
角度1利用绝对值的概念.因为
|a·e|+|b·e|=
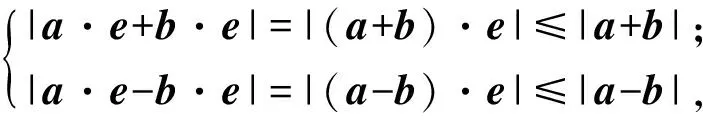

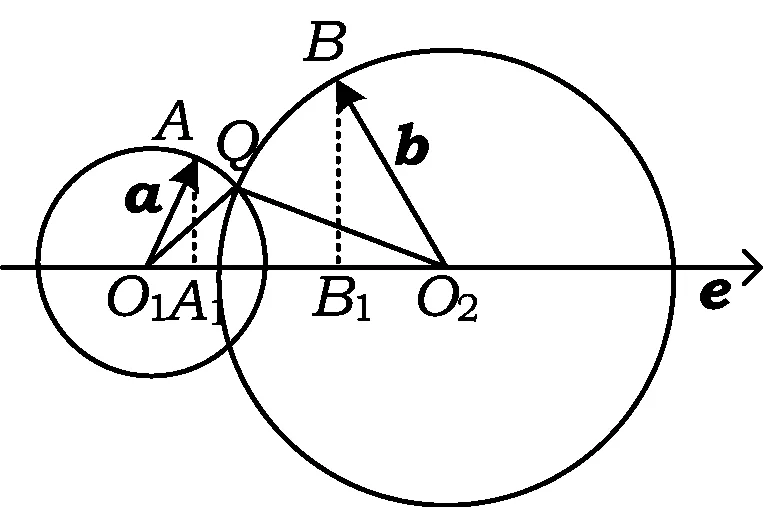
图1
3 关注变化与确定
数学中有些量是确定的,有些量是变化的,有些量的变化按某种特定规律,有些量的变化是随机的、不可预测的.而我们遇到的许多问题,都是在变化中进行的,若能发现变化中的不变量,并抓住其确定的数学本质,就可以使问题迎刃而解.
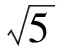
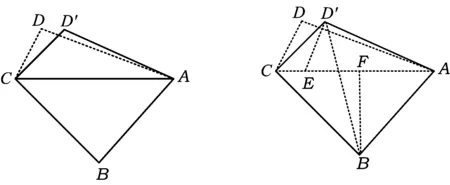
图2 图3
分析在图形变化的过程中,应寻找确定的关系、确定的量,来体现直线与直线所成角的变化规律.
本质1点B,D在AC上的投影确定.

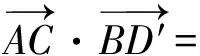
设θ为直线AC与BD′所成的角,则
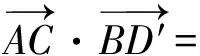
即

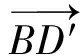
本质2点D的轨迹确定.
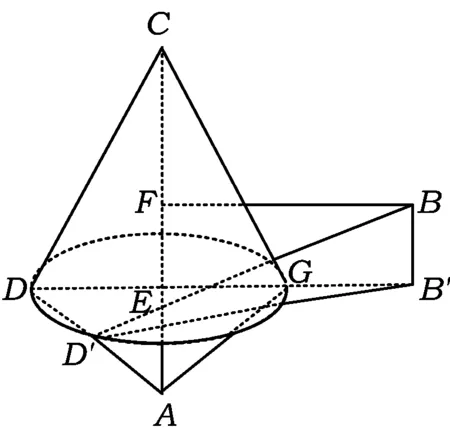
图4
四边形ABCD在沿直线AC将△ACD翻折的过程中,点D的轨迹是以E为圆心、DE为半径的圆.利用这一特点,可产生新的思路.
由题意,AC垂直于⊙E所在平面,作BB′垂直于⊙E所在平面,则直线AC与BD′所成的角就是直线BB′与BD′所成的角(如图4所示).要使cos∠B′BD′最大,就是要使B′D′最小,因为点D′在⊙E上,所以B′D′的最小值为
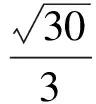
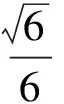
4 关注问题与表达
数学问题的表达形式多样,合理正确的表达使问题简洁明确.对问题表达的正确转化,也可使问题的本质更清楚.问题的解决也要合适表达,明确的思路可使表达更清楚易懂.
例4已知a≥3,函数F(x)=min{2|x-1|,x2-2ax+4a-2}.
1)求使得等式F(x)=x2-2ax+4a-2成立的x的取值范围.
2)①求F(x)的最小值m(a);②求F(x)在区间[0,6]上的最大值M(a).
分析本题对“函数F(x)的表达”的理解是解决问题的起点,已知条件把分段函数的表达形式巧妙地融合在了一起,更好地展示了F(x)这个函数的特点:取两个函数f(x)=2|x-1|和g(x)=x2-2ax+4a-2函数值小的部分.
1)等式F(x)=x2-ax+4a-2成立的x的取值范围,就是x2-2ax+4a-2≤2|x-1|成立的x的范围,很快求出不等式的解集为[2,2a].
2)由F(x)的含义可知,求F(x)的最小值m(a),就是求f(x)=2|x-1|和g(x)=x2-2ax+4a-2最小值的最小值,即
m(a)=min{f(1),g(a)},
故
求F(x)的最大值M(a).需抓住函数特点,从函数值的变化进行分析,抓住两个函数f(x),g(x)的图像都过定点(2,2)的特征.当0≤x≤2时,
F(x)≤f(x)≤max{f(0),f(2)}=2=F(2);
当 2 F(x)≤g(x)≤max{g(2),g(6)}= max{2,34-8a}, 故 数学问题的解决需要深刻的分析和仔细的计算.对所需解决的问题进行透彻分析,为后续计算提供正确的方法和简便的计算,精确的计算也为问题的直观分析、判断提供了证明[3]. 例5已知等差数列{an}的公差为d,等比数列{bn}的公比为q,设{an},{bn}的前n项和分别为Sn,Tn.若n2(Tn+1)=2nSn,其中n∈N*,则d=______,q=______. 分析这是一个常见的等差数列和等比数列问题,可以设两个数列的基本量来求解.因为等式n2(Tn+1)=2nSn对任意自然数n成立,所以可以让n取不同的值得到相应的等式.因为两个数列共有4个基本量,故可取n=1,2,3,4得到4个等式来求a1,d,b1,q.但计算不容易! 其实,在计算之前我们应先根据等差数列和等比数列前n项和的结构特点来分析思考:等差数列前n项和的形式一定是 等比数列前n项和的形式一定是 根据已知条件 由等式恒成立解得 数学的广泛运用,使人们对数学的重要性有深刻的认识.中学数学是数学的基础,但也和生活实际密切相关.我们可以从抽象的数学问题中体会到实际背景,也可从实际问题中提炼出数学问题并加以解决. 1)证明:|an|≥2n-1(|a1|-2). 分析此题看似是一个单纯的数列问题,其实它可以有多种不同的背景.例如,有一笔资金用于投资,若以后每一天的资金都比前一天翻一番且至多有2万元的误差,由此可得到结论:若有一天资金总值超过2万元,那么,资金总值将以2为底的指数爆炸式增长,或永远不超过2万元. 数学问题可以有许多种不同的表达形式和解决方法,但它的核心是清楚的、本质是不变的.只有抓住了问题的核心与本质,才能使问题的解决更清楚透彻. 推理与证明是人们思维活动的过程,是根据一个或几个已知的判断来确定一个新的判断的思维过程,是解决数学问题的重要手段.推理与证明相辅相成,密切联系.探索新的结论,并提供解决问题的思路和方法,感受推理与证明在数学中的作用,可以养成“言之有理,论证有据”的习惯. 1)an+1 分析该问题的证明形式多样,有等式也有不等式;证明手段多样,可以推理证明也可归纳证明,方法众多且各具特色. 于是 an+1 又因为a1=1,所以 因此,当n≥2时, 注:以上3个问题都可以用数学归纳法加以证明.8关注条件与转化 数学问题的条件形式多样,不同类型的条件有各自不同的作用:有些条件提供各种关系,有些条件提供一些数据,有些条件提供图像的特点等等.当我们从陌生的条件中整理出熟悉的线索、在条件之间发现它们之间的联系时,就抓住了问题的核心,整理出来就是解决问题的思路. 例8已知f(x),g(x)都是偶函数,且都在[0,+∞]上单调递增,设函数F(x)=f(x)+g(1-x)-|f(x)-g(1-x)| .若a>0,则 ( ) A.F(-a)≥F(a)且F(1+a)≥F(1-a) B.F(-a)≥F(a)且F(1+a)≤F(1-a) C.F(-a)≤F(a)且F(1+a)≥F(1-a) D.F(-a)≤F(a)且F(1+a)≤F(1-a) 分析理解函数F(x)=f(x)+g(1-x)-|f(x)-g(1-x)|的表达式是问题的关键.其实,为了把绝对值去掉,可以进行分类讨论,即可将F(x)理解为一个分段函数: 但这样的理解很难有进一步的解决策略. 从取绝对值的分类过程,可以理解为:F(x)=2min{f(x),g(1-x)},这样的表达将有助于我们解决问题.该问题的本质就是要比较F(a)与F(-a)、F(1-a)与F(1+a)的大小. 先来看看这几个函数值的特点: 1)比较F(a)与F(-a)的大小. 因为F(a)=2min{f(a),g(1-a)},F(-a)=2min{f(-a),g(1+a)},又已知函数f(x)是偶函数,从而 f(-a)=f(a); 于是 F(a)=2min{f(a),g(1-a)}, F(-a)=2min{f(a),g(1+a)}. 显然,要比较F(a)与F(-a)的大小,只要比较g(1-a)与g(1+a)的大小.已知g(x)是偶函数,那么g(1-a)=g(|1-a|).因此,当a>0时,只要比较|1-a|与1+a的大小即可.显然|1-a|≤1+a,那么F(-a)≥F(a). 2)比较F(1-a)与F(1+a)的大小. 根据F(a)与F(-a)的大小比较,因为 F(1-a)=2min{f(1-a),g(a)}, F(1+a)= 2min{f(1+a),g(-a)}= 2min{f(1+a),g(a)}, 而f(|1-a|)≤f(1+a),所以 F(1-a)≤F(1+a). 数学的教学需要我们认真思考、不断分析,既要抓住教学的重点、难点,也要关注考试的重点、方向,这样才能使我们的教学更加有效、高效. [1] 浙江省教育考试院.2017年浙江省普通高考考试说明[M]. 杭州:浙江摄影出版社, 2016(10):26-35. [2] 高考数学研究组. 浙江高考数学2004一路走来[M]. 杭州:浙江大学出版社,2016. [3] 朱伟义,曹凤山. 大道至简 悟者天成——2016年浙江省数学高考试题简析及有关高考复习的思考[J]. 中学教研(数学), 2016(8):36-39. 2017-01-15; 2017-03-03 冯 寅(1962-),男,浙江湖州人,浙江省特级教师.研究方向:数学教育. O12 :A :1003-6407(2017)07-42-04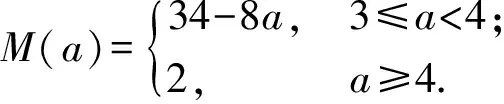
5 关注计算与分析
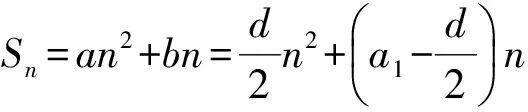
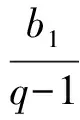
6 关注模型与应用
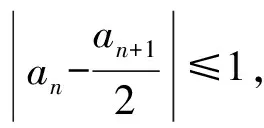
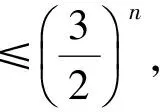
7 关注推理与证明