千年古图蕴藏题库
——阿基米德三角形演绎高考题

2017-07-01 22:12

中学教研(数学) 2017年7期

关键词：阿基米德切点切线

●

(南头中学广东深圳 518052)

千年古图蕴藏题库
——阿基米德三角形演绎高考题

●方亚斌

(南头中学广东深圳 518052)

作者介绍：湖北省特级教师，湖北省教育科研百佳个人之一，广东省南粤优秀教师，深圳市首批名师工作室主持人，深圳市政府特殊津贴专家,深圳市地方级领军人才, 深圳市首批中小学教师继续教育课程建设专家库入库专家，深圳市南山区高三数学名师工作室主持人.主持广东省、深圳市教科研课题3个，出版个人论著10余本，在30余家中学数学学科专业杂志上发表教育教学论文200余篇，其中10余篇被中国人民大学书报资料中心全文转载.多次获湖北省、广东省数学竞赛优秀教练员、深圳市高考先进个人称号.曾被聘为《中学数学》、《学科教育》等多家杂志社特约编辑、第2～4届“希望杯”全国数学邀请赛命题委员会委员.

文章以两个定理及推论的形式归纳出有关阿基米德三角形中点、线、面积的8条常用性质，从17个角度归纳出由阿基米德三角形衍生的5种类型的高考试题，探究同宗同源问题的命题规律和解题规律.

阿基米德三角形;高考题；性质；应用

1 阿基米德三角形的性质

抛物线的弦与过弦的端点的两条切线所围的三角形，称为阿基米德三角形.

阿基米德三角形的得名，是因为阿基米德本人最早利用逼近的思想证明了如下结论：

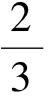
图1

为了后文的应用方便，我们先对阿基米德三角形相关性质做些归纳.下面的讨论，我们仅以抛物线x2=2py(其中p>0)为例，抛物线上两个不同的点A，B的坐标分别为(x1,y1)，(x2,y2)，以A，B为切点的切线PA，PB相交于点P，我们称弦AB为阿基米德三角形△PAB的底边(如图1所示).

2)底边AB所在的直线方程为

(x1+x2)x-2py-x1x2=0；

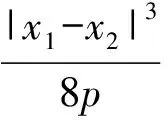
证明1)过点A,B的切线方程分别为

2)直线AB的斜率为

故直线AB的方程为

化简得

(x1+x2)x-2py-x1x2=0.

3)由定理1的1)，2)可得点P到直线AB的距离为

可得△PAB的面积

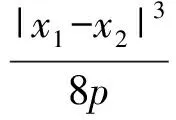
图2 图3

推论11)阿基米德三角形底边上的中线平行(重合)于抛物线的对称轴.

2)若点P的坐标为(x0,y0)，则底边AB的直线方程为x0x-p(y+y0)=0.

证明1)如图2，设点Q为底边AB的中点，由定理1可知，点P与点Q的横坐标相同，故PQ与y轴平行或重合．

2)将定理1结论2)中直线AB方程(x1+x2)x-2py-x1x2=0化为

可得

代入即得直线AB的方程为x0x-p(y+y0)=0.

从而

同理可得

于是

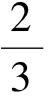
即

S△CAE=λS，

同理可得

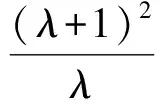
所以S△EAB=S△PAB-S△PCD-S△CAE-△DBE=

从而

图4

2)设C是阿基米德三角形△PAB的边PA的中点，过点C作抛物线的切线，切点为E，CE交PB于点D.由定理2，可得|CE|=|ED|，|PD|=|DB|.设Q为AB的中点,则点P,E,Q共线,且|PE|=|QE|.这表明在阿基米德三角形中，与底边平行的中位线是抛物线的一条切线，且切点就是这条切线与底边上中线的交点(如图4).根据此结论，可知

同理可得

对阿基米德三角形△AEC和△BED，分别作与底边平行的中位线，有与上面相同的结果，……类似这样无限操作下去，抛物线和弦AB围成的面积就等于无限多条边的凸多边形的面积，且可无限分割求和[1]，即

2 阿基米德三角形的应用

自公元前3世纪至今，历经了两千多年的风霜雨雪，阿基米德三角形尤如一颗闪烁的明珠，以其深刻的背景、丰富的内涵产生出了无穷魅力，在数学发展的历史长河中不断闪烁出真理的光辉.这个两千多年的古老图形，如同一个题库，里面蕴藏着各级各类考试命题和高考命题的素材.由阿基米德三角形衍生出的高考题，主要有以下5种类型：

2.1 线段长度问题

因此

视角2现考虑n个过抛物线x2=4y焦点F的阿基米德三角形△PiAiBi(其中i=1,2,…,n)，计算这n个三角形的顶点Pi到焦点F的距离之和，根据上面的结论，得

为了方便求和，不妨给定Ai的横坐标为xi=2i(其中i=1,2,…,n)，由等比数列求和公式得

|FP1|+|FP2|+…+|FPn|=

(2n-1)+(2-21-n)=2n-2-n+1+1.

从视角1和视角2切入,可编拟：

图5

题1如图5，对每个正整数n，An(xn,yn)是抛物线x2=4y上的点，过焦点F的直线FAn交一点Bn(sn,tn).

1)试证：xnsn=-4(其中n≥1)；

2)取xn=2n，并记Cn为抛物线上分别以An与Bn为切点的两条切线的交点，试证：

|FC1|+|FC2|+…+|FCn|=2n-2-n+1+1.

(2006年重庆市数学高考文科试题第22题)

视角4若再考虑阿基米德三角形△PAB的底边AB的长，则由定理1的证明过程可知

从视角3和视角4切入,可编拟:

图6

题2如图6，设抛物线方程为x2=2py(其中p>0)，M为直线y=-2p上任意一点，过M引抛物线的切线，切点分别为A,B．

1)求证：点A,M,B的横坐标成等差数列；

(2008年山东省数学高考理科试题第22题)

2.2 轨迹问题

视角5设阿基米德三角形△PAB底边AB的中点为Q，考查AB的中点Q的坐标与顶点P的坐标之间的关系.

2x2-2py,

从视角4和视角5切入,可编拟:

图7

1)求p的值；

2)当P在C2上运动时，求线段AB的中点Q的轨迹方程(当A,B重合于O时，中点为O).

(2013年辽宁省数学高考理科试题第20题)

视角7设阿基米德三角形△PAB的重心为G，考查重心G的坐标(x,y)与点P的坐标之间的关系，易知

于是

x-(4x2-3y)-2=0，

即

图8

显然kFA′·kPA=-1，从而FA⊥PA，由抛物线定义，得|AA′|=|AF|，故AP是线段A′F的中垂线，得

|PA′|=|PF|, ∠PA′A=∠PFA,

同理可证 |PB′|=|PF|, ∠PB′B=∠PFB,

从而

|PA′|=|PB′|=|PF|,

即

∠PA′B′=∠PB′A′，

于是 ∠PA′A= ∠PA′B′+90°=∠PB′A′+90°=

∠PB′B,

即

∠PFA=∠PFB.

从视角7～9切入,可编拟：

题4如图8，设抛物线C:y=x2的焦点为F，动点P在直线l:x-y-2=0上运动，过点P作抛物线C的两条切线PA,PB，且与抛物线C分别相切于点A,B.

1)求△APB的重心G的轨迹方程；

2)证明：∠PFA=∠PFB.

(2005年江西省数学高考理科试题第22题)

2.3 切线问题

视角10[3]考查阿基米德三角形△PAB在底边AB过y轴上定点C(0,y0)的条件下顶点P的轨迹.

设P(x,y)，则由定理1知

x1+x2=2x,x1x2=2py，

将C(0,y0)的坐标代入定理1中直线AB的方程可得

(x1+x2)·0-2py0-x1x2=0，

从而

x1x2=-2py0，

即

2py=-2py0，

根据推论1,阿基米德三角形底边上的中线平行(重合)于抛物线的对称轴，设Q为阿基米德三角形△PAB底边AB的中点，则过点Q且垂直于x轴的直线与直线l:y=-y0的交点就是阿基米德三角形△PAB的顶点P.

视角11[3]反之，若垂直于x轴的直线与AB和直线l:y=-y0分别交于点Q,M，可证明当MA是抛物线的切线时，点M就是阿基米德三角形△PAB的顶点，点Q也是△PAB底边AB的中点.

再代入切线MA的方程，可得

题5如图9，在平面直角坐标系xOy中，过y轴正方向上一点C(0,c)任作一直线，与抛物线y=x2相交于点A，B，一条垂直于x轴的直线，分别与线段AB和直线l:y=-c交于点Q,P.

1)若Q为线段AB的中点，求证：PA为此抛物线的切线.

2)试问第1)小题的逆命题是否成立？说明理由.

(2007年江苏省数学高考试题第19题)

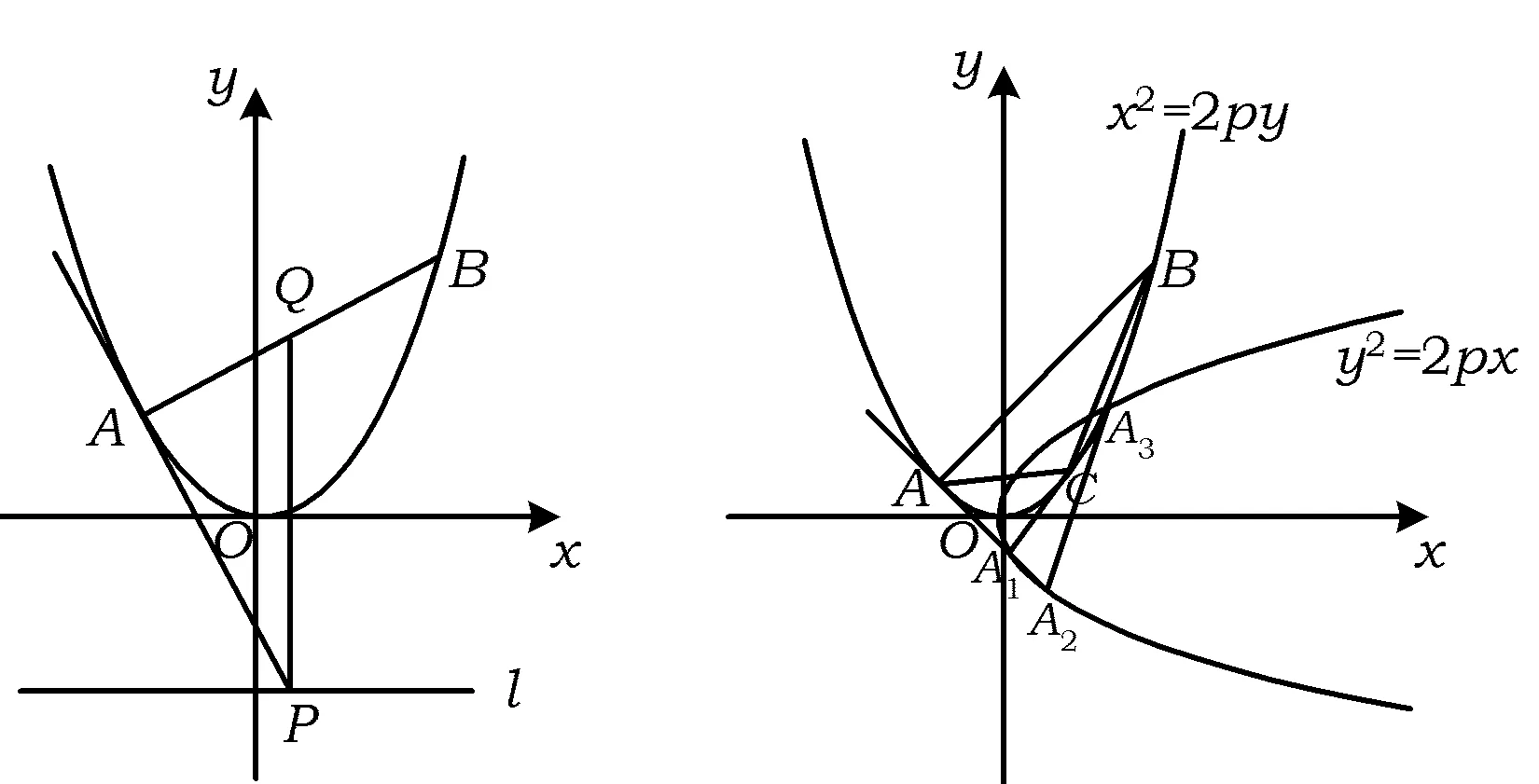
图9 图10

视角12[3]如图10，考查两条共顶点的抛物线y2=2px与x2=2py，假定抛物线y2=2px的内接△A1A2A3的边A1A2，A2A3所在的直线分别与抛物线x2=2py相切于点A，B，根据射影几何极点极线相关知识(共线点的极线必共点，共点线的极点必共线)，可知A1，A3相应于抛物线x2=2py的两极线(即过点A，B的切点弦)必共点，即△A1A2A3的边A1A3所在的直线与抛物线y2=2px相切于点C.

从视角12切入，可编拟：

题6抛物线y2=2px的内接三角形有两边所在的直线与抛物线x2=2py相切，证明这个三角形的第三边所在的直线也与x2=2py相切.

(1982年全国数学高考理科试题第8题)

2.4 最值问题

即

x1x2=-p2,

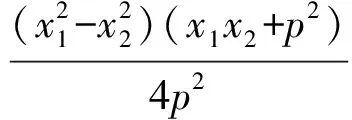
故PF⊥AB.

视角14设Q为AB的中点，根据推论1知PQ⊥x轴，于是

从视角13和视角14切入，可编拟：

2)设△ABM的面积为S，写出S=f(λ)的表达式，并求S的最小值.

(2006年全国数学高考卷Ⅱ理科试题第21题)

2.5 面积问题

视角15给定抛物线x2=2py上关于y轴对称的点A(-2,1)，B(2,1)，可求得其方程为x2=4y,且抛物线x2=4y在点A,B处的切线方程分别为y=-x-1，y=x-1，两切线的交点坐标为P(0,-1)，由推论2可知：若抛物线弧AB上任一点Q处的切线与PA,PB都相交，交点分别为D，E,则△QAB与△PDE的面积之比是常数2.

从视角15切入，可编拟: