双重最值问题的解法探究

●

(北仑中学 浙江宁波 315800)



双重最值问题的解法探究

●范东晖

(北仑中学 浙江宁波 315800)

文章从简单的一元双重最值问题入手，介绍解决双重最值问题的通性通法，包括数形结合与分段(分类)讨论；接着探究复杂的多元双重最值问题的解题策略，着重探究了算术(几何)平均、设而不求、先猜后证等方法.

一元(多元)函数；双重最值；求解策略

我们把形如“min{max{f(x1),f(x2),…,f(xn)}}”的问题称为双重最值问题，此类问题在数学高考和竞赛试题中屡屡出现.笔者通过实例来探究双重最值问题的一些解题策略.

1 一元双重最值问题

对于此类问题，笔者总结了5种方法，其中常用的两种基本方法是数形结合和分段(类)讨论.

1)求使得等式F(x)=x2-2ax+4a-2成立的x的取值范围.

2) ①求F(x)的最小值m(a);

②求F(x)在[0,6]上的最大值M(a).

(2016年浙江省数学高考理科试题第18题)

方法1数形结合.

解法11)g(x)=x2-2ax+4a-2过定点(2,2)，该定点又恰好在折线f(x)=2|x-1|的右支上，根据a≥3，以及函数

F(x)=min{2|x-1|,x2-2ax+4a-2}

的定义画出草图(如图1).只要分析右支f(x)=2(x-1)与二次函数的右交点，即

2(x-1)=x2-2ax+4x-2，

亦即

x2-2(a+1)x+4a=0,

其中1个根为2，容易求得另一个根为2a，故所求得的取值范围为[2,2a].

2)①由于二次函数的对称轴x=a≥3，函数的最小值即为

min{0,g(a)}=min{0,-a2+4a-2},

只要简单比较大小就可以了.

图1 图2

②求F(x)在[0,6]上的最大值M(a)，根据图像(如图2)可以看出，最大值的可能位置有3个，只要确定

min{0,f(2),f(6)}=min{2,34-8a}，

问题也就很简单[1].

方法2分段(类)讨论.

解法21)由于a≥3，故当x≤1时，

(x2-2ax+ 4a-2)-2|x-1|=

x2+2(a-1)(2-x)>0；

当x>1时，

(x2-2ax+4a-2)-2|x-1|=(x-2)(x-2a).因此，使得等式F(x)=x2-2ax+4a-2成立的x的取值范围为[2,2a]．

2)①设函数f(x)=2|x-1|，g(x)=x2-2ax+4a-2，则

f(x)min=f(1)=0,

g(x)min=g(a)=-a2+4a-2.

由F(x)的定义知

m(a)=min{f(1),g(a)},

即

②当0≤x≤2时，

F(x)≤f(x)≤max{f(0),f(2)}=2=F(2)，

当2≤x≤6时，

F(x)≤g(x)≤max{g(2),g(6)}=

max{2,34-8a}=max{F(2),F(6)},

因此

评注此题一题三问，含有参数，看起来挺复杂.实际上，只要思路清晰，运用数形结合、分类讨论思想，不断地转化问题，无论是解方程还是不等式，计算量都很少.

例2已知函数f(x)=x2-2(a+2)x+a2，g(x)=-x2+2(a-2)x-a2+8，H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}.max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值,记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=

( )

A.a2-2a-16 B.a2+2a-16

C.-16 D.16

(2013年辽宁省数学高考理科试题第11题)

分析本题中的A=min{max{f(x),g(x)}，B=max{min{f(x),g(x)}}.

f(x)=[x-(a+2)]2-4-4a，

g(x)=-[x-(a-2)]2+12-4a，

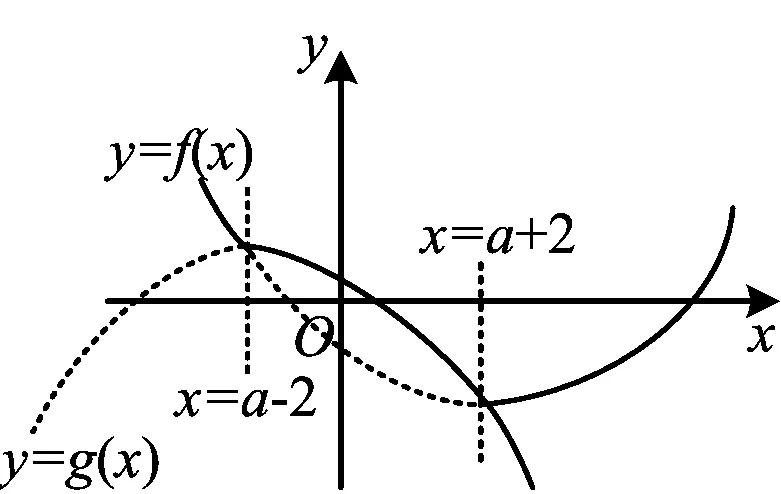
图3

在同一坐标系内作f(x)与g(x)的图像．依题意知，函数H1(x)的图像为实线部分，函数H2(x)的图像为虚线部分(如图3所示)，从而H1(x)的最小值为A=f(a+2)=-4-4a，H2(x)的最大值为B=g(a-2)=12-4a，因此

A-B=(-4-4a)-(12-4a)=-16.

故选C.

评注题中涉及两种双重最值，用数形结合在同一图像中可以同时直观显现，可谓“一箭双雕”.

2 多元双重最值问题

对于多元双重最值问题，解决一元双重最值问题所用的两种方法一般仍然适用，此外还有一些其他方法，如：

方法3利用算术(几何)平均.

(2011年河南省高中数学竞赛预赛试题第6题)

分析注意到，若设b=ta(其中t>0)，则

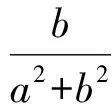
1)若a≥1，则

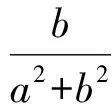
从而

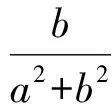
2)若0

方法4设而不求.

例4对任意的a,b>0，求

(2013年浙江高中数学竞赛试题第16题)

( )

当且仅当a=b=4c时等号成立.

①当c≤b≤4c时，

当且仅当b=c=4a时等号成立.

②当b≥4c时，

当且仅当a=b=4c时等号成立.

当且仅当b=c=4a时等号成立.故选C.

评注此题是多元条件背景下的双重最值问题.条件比较复杂，可进行分类讨论，综合运用不等式知识得以求解.

结合上述例子，对于多元双重最值问题，一般可以按照以下步骤解题：以min{max{f(x1),f(x2),…,f(xn)}}为例.

1)令M=max{f(x1),f(x2),…,f(xn)}；

2)可得M≥f(x1),f(x2),…,f(xn)；

3)消去x1,x2,…,xn得出关于M的不等式g(M)≤0；

4)解M≥A，且要使等号可以取到，A即为所求值[2].

方法5先猜后证.

对某些最值问题，可以根据问题的极端情形先猜出最值，然后用反证法证明之.

(1983年全国高中数学联赛试题二试第5题)

[1] 朱伟义，曹凤山.大道至简 悟者天成——2016年浙江省数学高考试题简析及有关高考复习的思考[J].中学教研(数学)，2016(8)：36-39.

[2] 吕辉.双重最值问题的解决探究[J].数学教学，2011(4)：31-32.

2017-03-19；

2017-04-20

范东晖(1973-)，男，浙江江山人，中学高级教师.研究方向：数学教育.

O122.1

：A

：1003-6407(2017)07-18-03