基于初中层面的弦张定点成直角的问题探究
●
(川汇区教体局教研室 河南周口 466001)
基于初中层面的弦张定点成直角的问题探究
●李世臣
(川汇区教体局教研室 河南周口 466001)
在动态数学软件GeoGebra环境下,文章以一道中考数学压轴题为起点,基于初中层面的抛物线、双曲线、平行直线、相交直线上的2个动点对某定点张直角问题进行了深入研究,发现一组有价值的结论,深化了对问题的认识.
GeoGebra;包络曲线;二次函数;反比例函数;轨迹
2014年湖北省武汉中考数学第26题是一道综合性较强的压轴题,其根植于初中核心知识和基本技能,指向于高中优生选拔和素养要求,是一道设计巧妙、简洁明了、内涵丰富的好题.文献[1]对曲线上的定点张直角弦问题进行了研究,若定点不在曲线上会有什么几何特征呢?笔者利用动态数学软件(GeoGebra)就基于初中层面的定点张抛物线上两点成直角问题、张双曲线上两点成直角问题、与两条平行线上的点张直角问题、与两条相交直线上的点张直角问题进行了拓展研究,获得了一些有价值的结论.

1)直线AB总经过一个定点C,请直接写出点C的坐标;

3)若在抛物线上存在定点D使∠ADB=90°,求点D到直线AB的最大距离.

图1 图2
问题3)说明抛物线上定点对抛物线上的弦张直角,则弦所在直线过定点.那么,这个问题能否推广到一般情况呢?
探究1平面内的定点张抛物线上两点成直角问题[2].
如图2,已知定点P(u,v),二次函数y=ax2+bx+c(其中a≠0)的图像与直线y=kx+d交于点A(x1,y1),B(x2,y2),∠APB=90°,PH⊥AB于点H(m,n).联立方程组
消去y,得ax2+(b-k)x+c-d=0,
则

过点H作对称轴的平行线,交抛物线于点G,设G(m,h),由点H在直线AB上,得
n=km+d.
由点G在抛物线上,得
h=am2+bm+c,
从而h-n=am2+(b-k)m+c-d=
a[m2-(x1+x2)m+x1x2]=
a(m-x1)(m-x2).
分别过点A,P,B,H作与坐标轴平行或垂直的直线,得垂足D,F,E,则
FH=v-n,EH=m-x2,DH=x1-m,
因为PH⊥AB,所以
△ADH∽△PFH∽△BEH.
又AP⊥PB,得
PH2=AH·HB,
即
FH2=EH·HD,


整理得





图3 图4


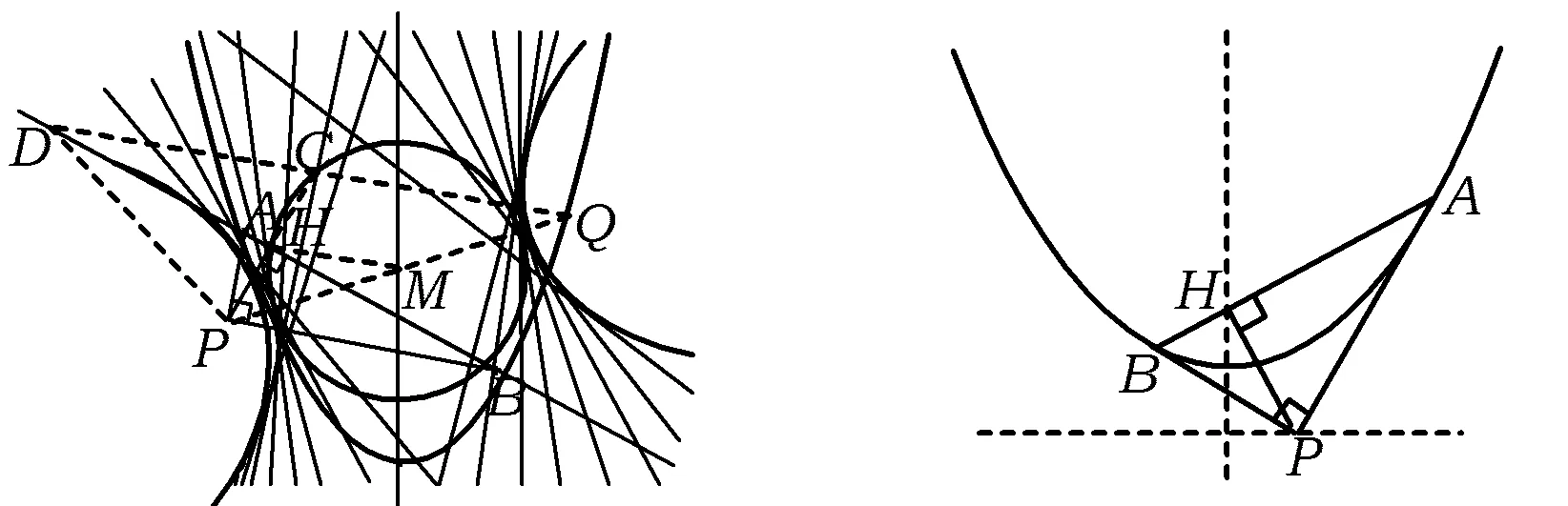
图5 图6

3)当时T<0,即点P与焦点S分布在抛物线准线的异侧,点P对抛物线的弦张直角不存在.
探究2平面内定点张双曲线上两点成直角问题[3].

图7
如图7,已知定点P(u,v),反比例函数xy=k(其中k≠0)的图像与直线y=ax+b交于点A(x1,y1),B(x2,y2),∠APB=90°,PH⊥AB于点H(m,n).联立方程组

消去y,得
ax2+bx-k=0,
则

由点H在直线AB上,得
n=am+b,
又由PH⊥AB,得



分别过点A,P,B,H作与坐标轴平行或垂直的直线,得垂足D,F,E,则
FH=v-n,EH=m-x2,DH=x1-m.
因为PH⊥AB,所以
△ADH∽△PFH∽△BEH,
又AP⊥PB,得
PH2=AH·HB,
即
FH2=EH·HD,
从而
(v-n)2= (m-x2)(x1-m)=

整理得
vm+un-uv-k=0.


图8 图9


探究3已知平面内定点与两条平行线上的点张直角问题.
已知m∥n,设直线m,n的间距为t,定点P到直线m,n的最近距离为s.点A,B分别在直线m,n上,∠APB为直角,PH⊥AB于点H.过点P作平行线m,n的垂线,得垂足为E,F,联结EH,FH,延长PH到点C,使HC=PH.取EF的中点M,点P关于点M的对称点为Q,作直线CQ交直线AB于点D.
1)当点P在直线m,n的异侧时,如图10,因为PE⊥AE,PH⊥AH,所以点A,E,P,H共圆,∠EHP=∠EAP.同理可得∠PHF=∠PBF,从而
∠EHF=∠EAP+∠PBF=∠APB=90°,
即点H在以EF为直径的圆上.
由中垂线和中位线的性质知,
DP+DQ=DC+DQ=QC=2MH=t(定值),
从而点D的轨迹是以P,Q为焦点、以EF为长轴的椭圆,是直线AB的包络曲线.
由于点P在点H轨迹圆的内部,于是
s 2)若点P在直线m(n)上,则点B(A)与点F(E)重合,∠EHF=90°,点H的轨迹是以EF为直径的圆(除点E,F).显然,0 图10 图11 3)当点P在直线m,n的同侧时,如图11,因为PE⊥AE,PH⊥AH,所以点A,P,E,H共圆,∠EHB=∠EPA.同理可得∠BHF=∠BPF,从而 ∠EHF=∠EPA+∠FPB=∠APB=90°, 即点H的轨迹是以EF为直径的圆. 由中垂线和中位线的性质知, |DQ-DP|=|DQ-DC|=QC=2MH=t(定值), 从而点D的轨迹是以P,Q为焦点、以EF为实轴的双曲线,是直线AB的包络曲线. 由于点P在点H轨迹圆的外部,因此 s 探究4已知平面内定点与两条相交直线上的点张直角问题. 1)定点在两条垂直直线的直角区域. 如图12,∠UOV=90°,PE⊥OU于点E,PF⊥OV于点F,PE=m,PF=n.点A,B分别在直线OU,OV上,∠APB=90°,PH⊥AB于点H,则点H在直线EF上,直线AB的包络曲线是抛物线,且 事实上,因为PE⊥OU,PH⊥AB,所以点A,E,H,P共圆,∠AHE=∠APE.同理可得∠BHF=∠BPF.又因为∠APB=90°,∠EPF=90°,所以∠APE=∠BPF,从而∠AHE=∠BHF,即点H在直线EF上. 图12 图13 2)定点在两条直线形成的锐角区域. 事实上,延长EP交直线OV于点J,延长FP交直线OU于点K,因为PE⊥OU,PF⊥OV,所以点E,F,J,K共圆,JK为该圆的直径,取圆心为M.联结EH,FH,因为PH⊥AB,所以点A,E,P,H共圆,∠EHP=∠EAP,同理可得∠PHF=∠PBF,从而 ∠EHF= ∠EAP+∠FBP=∠APB-∠AOB= 90°-θ=∠EKP, 即点H在定圆⊙M上. 延长PH到点C,使HC=PH,延长PM到Q,使MQ=PM.直线CQ,AB交于点D,联结PD,由中垂线和中位线的性质知PD=CD,CQ=2MH,从而 DP+DQ=DC+DQ=QC=2MH, 于是点D的轨迹是以P,Q为焦点、长轴长为JK的椭圆,是直线AB的包络曲线. 因为PM=MQ,KM=MJ,得四边形PJQK为平行四边形,所以JQ=PK,JQ∥FK,则JQ⊥OV.又因为∠KPE=∠JPF=∠EOF=θ,所以 PQ2= (PF-JQ)2+FJ2= 从而JK=2a,PQ=2c.由于点P在点H轨迹圆的内部,于是a-c≤PH≤a+c. 3)定点在两条直线形成的钝角区域. 如图14,∠UOV=θ(其中90°<θ<180°),PE⊥OU于点E,PF⊥OV于点F,PE=m,PF=n.点A,B分别在直线OU,OV上,∠APB=90°,PH⊥AB于点H,则点H在定圆上,直线AB的包络曲线是双曲线,且c-a≤PH≤c+a(其中a,c设置同上). 图14 事实上,延长PE交直线OV于点J,延长PF交直线OU于点K,因为PE⊥OU,PF⊥OV,则点E,F,J,K共圆,JK为该圆的直径,取圆心为M.联结EH,FH,因为PE⊥OU,PH⊥AB,所以点A,E,P,H共圆,∠PEH=∠PAH,同理可得∠PFH=∠PBH.在凹四边形PEHF中, ∠EHF= ∠PEH+∠PFH+∠EPF= ∠PAH+∠PBH+90°-∠EJF= 180°-∠EJF, 即点H在定圆⊙M上. 延长PH到点C,使HC=PH,延长PM到Q,使MQ=PM.直线CQ,AB交于点D,联结PD,由中垂线和中位线的性质知PD=CD,CQ=2MH,从而DP+DQ=DC+DQ=QC=2MH, 于是点D的轨迹是以P,Q为焦点、实轴长等于JK的椭圆,是直线AB的包络曲线. 易得四边形PJQK是平行四边形,于是JQ=PK,JQ∥FK,JQ⊥OV.因为∠KPE=∠JPF=∠EOF=180°-θ,所以 JK2=KF2+FJ2= PQ2= (PF+JQ)2+FJ2= 于是JK=2a,PQ=2c.由于点P在点H轨迹圆的外部,从而c-a≤PH≤c+a. 波利亚有过一个比喻:“好问题如同某种蘑菇,它们大都成堆地生长.找到一个以后,你应当在周围找一找,很可能在附近就有好几个.”这个比喻形象而生动地说明了数学问题之间存在着紧密联系.本文从一道中考压轴题出发,借助数学技术,在问题解决之后,通过类比、迁移发现证明了定点张常规曲(直)线上的点成直角的几何特征,深刻揭示了其内在规律,如同找到了更多的蘑菇,举一反三、闻一知十. [1] 李世臣.一道中考数学压轴题的探究与推广[J].数学教学,2016(1):25-29. [2] 李世臣,陆楷章.圆锥曲线对定点张直角弦问题再研究[J].数学通报,2016(3):60-64. [3] 朱寒杰.由一道双曲线试题引起的探究与思考[J].中学教研(数学),2013(12):14-16. 一方面,高三学生已学过了高中数学的所有知识和基本技能,解题经验也比高一、高二的学生要丰富,对于问题的分析与思考能够更深入;另一方面,在课堂时间的安排上,高三阶段可以花更多的时间在问题的探索、解决、比较、综合等高层次的思维活动中,而不必担心教学进度的问题.因此,可以利用这两方面的优势来设计我们的课堂教学,以实现继续发展学生数学核心素养的目标.笔者在第一轮复习中以小专题的形式上了一节“立体几何轨迹问题”,下面以这节课的几个片断为例谈几点认识,以求教于同仁. 3.1 通过师生互答,引导学生审题 图1 片断1PPT放映题目,师生共同分析题意. 例1如图1,斜线段AB与平面α所成的角为60°,B为斜足,平面α内的动点P满足∠PAB=30°,则点P的轨迹是 ( ) A.直线 B.抛物线 C.椭圆 D.双曲线的一支 (2015年浙江省数学高考理科试题第7题) 师:已知条件有哪些?这些条件中哪些是变量,哪些是常量?需要我们做些什么? 生1:条件“AB与平面α所成的角为60°”是常量,P是动点,是变量,它要满足∠PAB=30°,我们的任务是求点P的轨迹. 生2:条件中还有“点P在平面α内”“∠PAB=30°”也是常量. 师:嗯,分析得不错.这是一个以立体几何为载体求轨迹的问题,根据条件你们能想象它们在空间的情形吗?能否用身边的物件来摆一个符合题意的示意模型? (教师让一个学生在讲台上展示,他用两支笔和一本书摆了个模型.) 师:非常好,刚才我们也说到这是动点P的轨迹问题,那么哪些条件是限制动点P的呢? 生3:点P需满足既在平面α内又要使∠PAB=30°. 师:你能想象点P是怎么运动的吗? (生3沉默.) 生4(同时用两支笔示意了转动情形):如果只考虑∠PAB=30°,那么点P在以AB为轴、PA为母线的圆锥面上.另外,点P又要平面α内,因此点P应该在圆锥与平面的公共线上. 师:你们看呢? 生3:对啊,这样就变成一个圆锥面与一个平面的交线了. 3.2 鼓励交流讨论,展现学生风采 片断2画图法描述7种情形. 教师在让学生回忆“一个平面截圆锥得到什么曲线”时,生5在黑板上画出了图2~4: 图2 图3 图4 师:请解释一下你画的图. 生5:我是画出了圆锥的轴截面,就是这两个三角形,这条直线表示从侧面去看平面:当平面与一条母线平行时得到的是抛物线(图2),当平面与圆锥的一侧相交时得到椭圆(图3),当平面与圆锥的两侧都相交时得到双曲线(图4). 师:大家能想象吗?生5的这种画图法比画立体几何直观图要方便得多,他把立体几何问题平面化了,并凸显了关键元素. (此时,教师用Flash演示3D模式下的圆锥曲线,帮助空间想象能力较弱的学生想象). 师:刚才还有同学说到有可能得到圆与直线,哪位同学可以进行补充? 生6出乎意料地补充了图5~8,然后指着对应的图解释到:当平面与圆锥底面平行时得到圆,当平面过圆锥顶点且不与底面相交时得到一个点,当平面过顶点且与底面相交时得到两条相交直线,当平面经过一条母线时得到一条直线. 图5 图6 图7 图8 听完生6的发言,传来一片赞叹声.此时有一个学生问到:你在解释图6时说平面与圆锥底面不相交,可看上去会相交啊. 生6(沉默了一会儿):因为我们这里说的圆锥并不是立体几何中的圆锥体,应该是圆锥曲面,不研究它的底,也可认为没有底.就像题目中要求的点P是在圆锥面上. 生7:既然没底,那不是不能说与底相交或是不相交了? (生6想反驳但又想不出说什么.) 师:生6补充得非常完整,只是他用数学语言描述时出了点小问题,被细心的同学发现了,那么,我们是不是可以讨论一下,从什么角度可以更方便地描述这7种情况? 学生通过交流与讨论,表达了自己的描述方法,这里列举两种认同度最高的描述方法: 方法1利用与圆锥的轴所成角的大小来描述. 如图9,设圆锥母线与轴所成角的大小为θ,轴与平面所成的角为α.1)在平面不过圆锥顶点的情况下:①当0°<α<θ时,交线为双曲线;②当α=θ时,交线为抛物线;③当θ<α<90°时,交线为椭圆;④当α=90°时,平面与圆锥曲面的交线为圆.2)在平面过圆锥顶点的情况下:①当0°≤α<θ时,交线为两条直线;②当α=θ时,交线为一条直线;③当θ<α≤90°时,平面与圆锥曲面的交线为一个点. 图9 图10 方法2虚构底面,借助平面与底面的较小的二面角大小来描述. 如图10,生6把自己的表达修改了一下,他认为可以虚构一个底面,用虚线表示,借助平面与底面的较小的二面角大小来描述上述7种情形. 3.3 反思解题过程,提高解题水平 片断3教师引导学生解决例1,并尝试设计新题. 师:哪位同学能用平面图解释一下例1? 生8(画图后回答):利用方法1.如图11,母线与轴的夹角为30°,平面退化的直线与轴的夹角为60°,大于母线与轴的夹角,因此交线为椭圆. 图11 师:完全正确.回忆一下自己的解题思路,你在思考过程中有没有受阻?受阻的原因是什么?你认为解决例1的关键是什么? 学生通过分析,得到解决立体几何轨迹问题的方法:先把满足的条件分开考虑,想象满足单个条件的轨迹,然后求这些轨迹的交线.由于该方法与轨迹方程中的交轨法类似,就称为“交轨法”. 师:能在此基础上设计出不同的题目,其答案为其他选项吗? (有些学生改变AB与平面所成角的大小,有些学生改变∠PAB的大小,都实现了编题目标.) 3.4 分析对比解法,归纳猜想通法 片断4通过两道练习题,辨析提升. 练习1在正方体ABCD-A1B1C1D1中,P是侧面BB1C1C内一动点,若点P到直线BC与直线C1D1的距离相等,则动点P的轨迹所在的曲线是 ( ) A.直线 B.圆 C.双曲线 D.抛物线 (2004年北京市数学高考理科试题第4题) 练习2已知平面ABCD⊥平面ADEF,AB⊥AD,CD⊥AD,且AB=1,AD=CD=2.四边形ADEF是正方形,在正方形ADEF内部有一点M,满足MB,MC与平面ADEF所成的角相等,则点M的轨迹长度为 ( ) 教师先让学生独立解答5分钟,再让学生回答.接着,小组交流下面3个问题,让各组代表说说解法并进行点评: 1)你觉得这两道题能否用例1的解法解决?为什么? 2)这两道题的解法有什么共同之处和不同之处? 3)通过这两道题的解决,你获得了什么经验? 课后思考:能否对这两道练习题进行改编,设计出不同的题目,其答案为其他选项. (练习1和练习2的答案分别为D和C.这两道题都是把条件转化到同一平面中去解决:练习1转化后可直接用抛物线定义轻松解决;练习2转化后不容易找几何关系,因此可建立平面直角坐标系,用解析几何的方法来解决.) 4.1 利用身边事物,培养数学眼光 让学生学会用数学的眼光去看世界,是核心素养培养的目标之一.在本课中,笔者让学生用身边的物件来示意例1中条件所要求的点、线、面位置关系,把笔、纸、桌面、书本等抽象成直线与平面就是对客观事物的数学抽象,这在立体几何教学中是非常容易实现的.例如学生所处的教室可抽象成长方体、棱柱等几何体,教室内还可抽象出很多点、线、面的位置关系,若在平时的教学中教师能有意识地加以引导,则将有利于发展学生的数学抽象素养,并学会用数学的眼光去看世界. 4.2 根据专题内容,发展相应素养 每个专题会涉及各自的知识点、解题方法与思想方法,教师在备课中应根据各专题特点精选例题进行设计,以促进学生相应数学核心素养的发展.本专题内容在知识体系中处于立体几何与解析几何的交汇处,可以作为发展学生直观想象的载体.由于在数学感知中,绝大多是视觉感知[2],因此对于立体几何问题,要在头脑里形成抽象的数学模型,最好的方法就是先从具体模型入手. 笔者先让学生用身边的事物构造出符合条件的模型,然后让学生用平面图进行分析,这是立体几何平面化思想的体现,同时又让学生经历了利用图形描述、理解、探索、解决数学问题的过程.直观想象是发现和提出数学命题、理解数学命题、探索论证思路的重要辅助手段.在数学教学活动中,若教师重视和加强学生在这方面的引导,则将有利于学生养成运用图形和空间想象思考问题的习惯,有利于学生提升数形结合的能力,有利于学生形成借助图形和空间进行分析、推理、论证的能力. 4.3 创造交流机会,发展数学表达 每个数学核心素养水平的阐述,都会涉及思维与表达、交流与反思[1].学生要表达自己对某个问题的想法就需要对问题进行数学抽象、直观想象、逻辑推理等处理,而在听取他人的表达时又需要理解别人的表达并进行分析,这个过程可以较好地反映出学生的数学素养,高三学生在数学表达上具备了一定的基础,实施起来更加容易.在学生相互合作、相互说服的过程中,气氛会比面对教师要轻松得多,如此,学生可以更大胆地表达自己的观点,在展示他们亮点的同时暴露出他们在表达上的不足.此时,教师加以引导或修正,更有利于发展学生的数学表达与理解能力,有利于发展他们的数学素养. 4.4 引导解题反思,提升思维品质 在高三阶段,为了节省教学时间,提高学生的应试水平,教师常常会把一些有针对性的解法或是通法直接告诉学生,再让学生加以练习运用.如此,学生只是去理解、记忆、应用教师归纳总结出的结论.根据布鲁姆认知目标分类的6个层次“知道—领会—应用—分析—综合—评价”可知:“直接告诉答案”只是让学生的思维停留在前3个低阶思维层次,浪费了发展学生核心素养的机会.因此,笔者尝试用好这一机会,在每个例题后设置了几个问题,引导学生进行解题反思,引导学生分析、比较已获知的解题方法,归纳猜想出适合立体几何轨迹问题的一般性解题思路.长此以往,可以使学生的思维上升到“分析、综合”甚至更高的“评价”层次,同时又能让学生体验数学发现的乐趣,从而更喜欢数学. 在高三数学教学中,教师以小专题、微专题形式,引导学生进行探究与反思,并提供学生间合作交流的机会,使学生在交流中逐步暴露自己在学习中的难点、疑点,然后在生生互动、师生互动中帮助学生突破难点、解决问题,如此,可让学生更好地掌握基本知识与基本技巧,体会其中蕴含的数学思想,久而久之,可使学生的数学核心素养水平得到真正的提高. 参考文献 [1] 王尚志.高中数学课程标准修订背景与学科核心素养[R].全国中小学教师继续教育网,2016. [2] 吴增生.3B教育理念下的数学高效课堂教学策略初探[J].数学教育学报,2011(1):17-22. 2017-03-16; 2017-04-18 河南省教育科学“十三五”规划课题(2016-JKGHB-1076) 李世臣(1964-),男,河南项城人,中学高级教师.研究方向:数学教育. O123.1 :A :1003-6407(2017)07-34-05





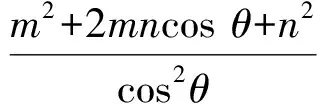




2 问题分析
3 实施案例






4 几点认识
5 结束语

