概率统计中样本空间刍议

◎周海林

(江苏省泰州市南京理工大学泰州科技学院，江苏 泰州 225300)

一、引 言

概率论与数理统计是一门研究随机现象统计规律的科学样本空间是概率中的一个基本概念，但是在概率学习中却往往被忽视这导致在概率统计的教学过程中，不少学生反映学习难度大，特别是在古典概型的计算上除了思维方式与高等数学和线性代数不同外，样本空间的选取在这些问题的解决中往往起着非常重要的作用本文对样本空间概念及其选取进行了一些思考与总结

二、样本空间概述

样本空间的概念来源于统计学，它由统计学家冯·米泽斯(Von Mises，1883—1953)于二十世纪三十年代在采用集合论的观点研究事件时引入

我们将随机试验的所有可能结果组成的集合称为样本空间，记为样本空间的元素，即的每个可能结果，称为样本点一般来讲，讨论的问题不同，样本空间可以很简单，也可以十分复杂在具体问题中，给定样本空间是描述随机现象的第一步不过我们常常认为样本空间是预先给定的这是一种必要的抽象，这种抽象不仅能让我们更好地把握随机现象的本质，而且得到的结果能更广泛地得到应用事实上，一个样本空间可以概括各种实际内容不同的问题例如，只包含两个样本点的样本空间，既可以作为抛掷硬币出现正面、反面的模型，也能用于产品检验中出现“正品”及“次品”，还能用于射击中描述“中”与“不中”等尽管问题的实际内容如此不同，有时却能归结为相同的概率模型

有了样本空间，就可以定义随机事件随机事件可定义为样本点的集合，这样，事件间的关系及运算就与集合论中集合的关系及运算完全类似概率论的重要研究课题就是计算概率，这最终都归结为事件的概率计算

现代概率论建立在集合论的基础上概率问题的复杂程度和所使用的数学工具的高低都主要取决于样本空间的大小因此，样本空间实际上是按集合的大小归类的，它可分为有限集、可列集等在有限样本空间中，概率论使用的数学工具主要是初等数学；在可列样本空间中，要用到级数；在欧几里得空间中，则广泛使用微积分

作为有限样本空间的一种特例，古典概型由法国数学家拉普拉斯在1812年提出，并把下式作为古典概率的一般定义：

上式中，事件的概率是一个分数，其分母是样本空间样本点的总数，而分子是事件所包含的样本点的个数，也称有利场合数

三、应用样本空间计算古典概率

要成功解决古典概率计算问题，必须用合适的样本空间来描述随机试验，而明确在怎样的样本空间下解题是第一步，也是最基本的一步因此，我们首先要把问题归结为一个随机试验，明确该试验的所有可能结果，即样本点，然后在此基础上给出相应的样本空间

(一)正确写出描述随机试验的样本空间

1将一枚硬币抛掷三次，考察出现正面、反面的情况

(1)设事件为“恰好出现一次正面”，求()；

(2)设事件为“至少出现一次正面”，求()

(1) 由题意知样本空间为

={,,,,,,,}，

而={,,}

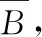
2抛掷两枚硬币，求出现正面和反面各一次的概率

注：当样本空间的元素较多时，一般不再将样本空间中的元素一一列出，而只需分别求出样本空间与事件中包含的元素的个数(即样本点个数)，再利用公式求出事件发生的概率

因此，在构造样本空间计算古典概型中事件发生的概率时，需要注意每个样本点出现的可能性必须是相等的这个要点称为等可能性

(二)选择合适样本空间，优化概率计算

对于同一随机试验，样本点和样本空间的选取并不唯一我们可以用不同的样本点和样本空间来描述随机试验，这取决于如何看待实验的结果但不管用什么样的样本空间来描述，所关心的某一事件发生的概率应该是一样的

3袋中有只黑球和只白球，把球随机地一只只摸出来，求第次摸出黑球的概率(1≤≤+)

通过比较三种不同的解法，我们就会发现区别主要在于选取的样本空间不同在第一种解法中，球被看成是有“个性”、有区别的，且按次序排列；在第二种解法中，则对同色球不加区别因此，第一种解法要考虑各黑球间及各白球间的顺序而用排列，第二种解法不注意顺序而用组合，解法三则仅仅关注第次摸球的结果，但最后都得出了相同的答案显然，解法三中构造的样本空间是最简洁的，解法也是最简单的

此外,从这个例子还可以看出，第二种解法中的每一个样本点是由第一种解法中的!·!个样本点合并而成的因此，样本点的不可分性是相对的

最后，在计算样本点总数及有利场合数时，必须在同一个样本空间中考虑，否则会引起混淆而导致谬误

显然，构造不同的样本空间，计算概率的难易程度有差别，下面再举几例

4袋中有只黑球和只白球，从袋中每次摸出一只球，直到袋中剩下的球全是同色为止，求袋中剩下的球全是黑球的概率

显然，这样可以做出来，但比较麻烦

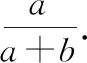
5投掷一枚均匀的硬币(2+1)次，求掷出的正面数比掷出的反面数多的概率

由于每次掷出正面和反面的可能性是一样的，由乘法原理知样本空间有22+1个样本点本题应用组合系数虽然可以做出来，但比较麻烦

事实上，可以这样考虑：记={掷出的正面数>掷出的反面数}，={掷出的反面数>掷出的正面数}，显然，事件与事件处于对称平等的位置，发生的可能性应该相等，即()=()

6袋中装有(2-1)只白球和2只黑球，一次取出只球，发现都是同一种颜色，求这种颜色是黑色的概率

注：尽管对事件发生有利的样本点与在事件发生的条件下对事件发生有利的样本点是一样的，但是概率的计算是在不同的样本空间中进行的显然，条件概率是在一个缩小的样本空间中进行计算的

7任取一个正整数，求该正整数的平方能被5整除的概率

本题按常规思路是研究所有正整数，也就是将正整数的全体作为样本空间，显然，这样的样本空间是无限空间，也谈不上等可能性这样，它就不是一个古典概型了那么，要将它化为一个古典概型，关键在于如何将无限样本空间缩减为有限样本空间，同时满足等可能性要求

四、应用样本空间计算几何概率

在前面古典概型的讨论中，我们利用等可能性的概念，成功计算了这类问题的概率不过，古典概型要求样本空间中的样本点总数必须有限下面我们讨论有无限多结果而又有某种等可能性的场合，这类问题一般可以通过几何方法来求解不过，这种等可能性是通过下列方式来赋予意义的：落在某区域的概率与区域的测度(长度、面积、体积等)成正比，并且与其位置及形状无关

因此，若以记“在区域中随机地取一点，而该点落在区域中”这一事件，则其概率定义为：

在几何概型中，若所考虑的问题只有一个因素在变，则取长度作为几何度量；若所考虑的问题有两个因素在变，则取面积作为几何度量；若所考虑的问题有三个因素在变，则取体积作为几何度量

我们不难发现：在几何概型中，结果为无限不可数个，且样本空间中的事件的概率与该事件的几何度量成正比，而与它的位置无关这是随机变量服从均匀分布的实际背景

8在[0,1]中任取两个数，求下列事件的概率：

(1)两数的和不超过15；(2)两数的积不超过025

设两数分别为，，则0≤≤1，0≤≤1

对于几何概率问题，贝特朗于1899年在《概率论》一书中介绍了一个实例——贝特朗奇论，引起了大家的注意，推动了概率论的发展

(1)如果认为弦的端点等可能地落在圆周上，则一点确定后，另一点也等可能地落在圆周上以此点为顶点作一等边三角形，显然，只有落入此三角形内的弦才满足要求，这种弦的另一端跑过的弧长记为，则

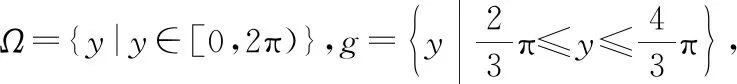
注意：同一问题有三种不同的答案，细究原因，我们会发现在取弦时采用的等可能性假定不同三种答案针对的是三种不同的随机试验，对应三种不同的样本空间，才导致有不同的计算结果但对于各自的随机试验而言，它们都是正确的

五、结束语

样本空间是一个重要的基本概念，教师在教学中需要循序渐进地增强学生对它的理解和应用特别是在古典概型的计算上，尽管对同一问题可以用不同的样本点和样本空间来描述，但是对同一事件的概率计算难易程度在不同的样本空间中会有比较大的差别其实，概率问题的复杂程度与所需要使用的数学工具主要取决于所选取样本空间的大小显然，上面几个例题中最简单的解法中所选取的样本空间都是最小的了如果还要小的话，所求概率的事件就“装”不进样本空间，即所求事件不是样本空间的子集，或者无法保证等可能性因此，抓住刻画所求概率事件的本质特点，对与其关系不大的因素不予考虑，恰当地选取样本点和样本空间，将有助于更快更容易地正确解决问题