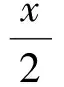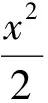导数压轴题的关键在运算

●

(新疆生产建设兵团第二中学 新疆乌鲁木齐 830002)



导数压轴题的关键在运算

●徐波

(新疆生产建设兵团第二中学 新疆乌鲁木齐 830002)

以往认为解决导数压轴题的关键是分类讨论.根据多年的研究和实践，文章提出解决此类问题的关键是运算.整个解题的进程和解题方案的形成背后其实都是受运算进程支配，运算在其中起着决定性作用.

导数压轴题;运算；最值；极值

文献[1]中提出解决导数压轴题的关键是分类讨论的观点，笔者根据多年来研究高考试题和参加高三模考命题的实践，切身体会到解决导数压轴题的关键是运算.每当碰到运算不下去或者运算的关键转折点时才需要分类讨论，整个解题的进程和解题方案的形成背后其实都是受运算进程支配，运算在其中起着决定性作用.

《高考大纲》指出：“运算求解能力是思维能力和运算技能的结合，运算能力包括分析运算条件、探究运算方向、选择运算公式、确定运算程序等一系列过程中的思维能力，也包括在实施运算过程中遇到障碍而调整运算的能力.”[2]这些对运算能力的要求贯穿于解决导数压轴题的全过程中，运算求解能力、推理论证能力、创新意识等综合体现在导数压轴题的求解过程中，以达到对考生进行深层次考查的目的[3-4].

笔者选择了近几年新疆乌鲁木齐市高三诊断性测试题作为素材来展开论述.在分析试题的解题思路时，笔者尝试将思路形成过程记录下来，希望收到更加真实、亲切、自然的效果.为了增加实用性，在每道例题分析之后，增加一道相应的练习题，希望能对广大师生有所帮助.

例1已知函数f(x)=ex+ln(x+1)．

1)求曲线y=f(x)在点(0,f(0))处的切线方程；

2)当x≥0时，f(x)≥ax+1成立，求实数a的取值范围．

(2016年新疆乌鲁木齐市高三年级第一次诊断性测验数学理科试题第21题)

分析1)按常规套路去做.由题意得

f(0)=e0+ln(0+1)=1，

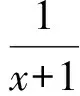
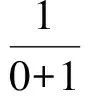
于是y=f(x)在点(0,f(0))处的切线方程为

y-1=2(x-0)，

即

y=2x+1.

第1)小题为第2)小题埋下了伏笔，既然曲线y=f(x)在点(0,f(0))处的切线方程为y=2x+1，按照几何直观得知曲线y=f(x)在切线y=2x+1的上方，也就是当x≥0时，f(x)≥2x+1恒成立.现在要想使得当x≥0时，f(x)≥ax+1恒成立，只要直线y=ax+1比切线y=2x+1“压得还低”就行了，也就是a≤2即可，这时已经“猜”到了答案.

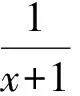
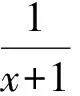
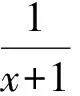
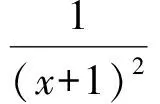
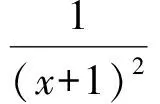
h′(x)>0，

于是函数y=h(x)在[0，+∞)上为增函数，即

h(x)≥h(0)=2，

亦即

g′(x)≥2-a.

①当a≤2时，2-a≥0，g′(x)≥0,从而函数y=g(x)在[0，+∞)上为增函数，于是g(x)≥g(0)=0.此时，对任意x≥0，f(x)≥ax+1成立.

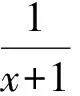
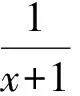
②当a>2时，a-1>1，由于x≥0,从而

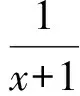
当x∈(0,ln(a-1))时，

ex+1-a<0，

即

g′(x)<0，

从而函数y=g(x)在(0,ln(a-1))上为减函数，于是当0

g(x)

因此，f(x)

综上所述，对任意x≥0，f(x)≥ax+1成立时，实数a的取值范围为(-∞,2].

1)若曲线y=f(x)在点(0,f(0))处的切线与直线x-2y+1=0平行，求a的值；

(2016年新疆乌鲁木齐市高三年级第一次诊断性测验数学文科试题第21题)

2)试讨论函数y=f(x)的零点个数．

(2016年新疆乌鲁木齐市高三年级第二次诊断性测验数学理科试题21题)

当-10，从而

g′(x)≥0，

此时函数g(x)单调递增，于是

g(x)≤g(0)=0，

2)要讨论函数的零点个数，必须先摸清楚这个函数的单调性和极值情况.

①当m=1时，x1=x2=0，由式(1)得

从而当x>-1时，1+x>0，x2≥0，于是

f′(x)≥0.

此时函数f(x)为增函数,因此当-1

f(x)

当x>0时，

f(x)>f(0)=0，

函数y=f(x)在x>-1上有且只有一个零点x=0.

图1

(2)

构造函数k(x)=lnx-x+1(其中x>0)，则

当01时，k′(x)<0，从而函数y=k(x)的增区间为(0，1],减区间为(1,+∞)，于是

k(x)≤k(1)=0，

即

lnx≤x+1,

从而

即

故

(4)

由式(3)和式(4)知

(5)

图2

综上所述,当01时，函数y=f(x)有两个零点;当m=1时，函数y=f(x)有且仅有一个零点．

2)当m≤1时，试讨论函数y=f(x)的零点个数．

(2016年新疆乌鲁木齐市高三年级第二次诊断性测验数学文科试题第21题)

导数压轴题，关键在运算.在平常的教学中讲解习题或者试卷的时候，每当碰到运算不下去或者运算的关键转折点时，教师要停下来，把学生“卡”在那里，让他们左冲右突、尝尽苦头，然后再适时进行点拨，提炼出解决问题的关键思路和技术.

这里常常借助函数的泰勒展开式或者麦克劳林展开式，将一个超越函数用一个有理函数去取代，有时还需要做一些变量代换，以获得我们所需要的形式.整个题目的探究进程和解题方案的形成背后其实都是受运算进程的支配，运算在其中起着决定性作用.希望大家在运算的实践中不断地磨炼和提升，积累体验，获取经验，把导数压轴题解好.

[1] 龙正武，谭国文.怎样更好地做好导数大题的答题准备[J].中国数学教育:高中版，2012(1/2)：67-83．

[2] 教育部考试中心.2016年普通高等学校招生全国统一考试大纲[M].北京：高等教育出版社，2015：50-53.

[3] 教育部考试中心.2016年普通高等学校招生全国统一考试大纲的说明[M].北京：高等教育出版社，2015：131-132.

[4] 教育部考试中心.高考理科试题分析[M].北京：高等教育出版社，2015:135-138.

2017-03-15；

2017-04-16

徐 波(1964-)，男，四川大竹人，新疆自治区特级教师.研究方向：数学教育.

O122.1

：A

：1003-6407(2017)07-30-04