用构造法求数列通项公式的探讨

云南省保山第一中学 杨竹青

数列中蕴含着丰富的数学思想，而递推数列的通项问题具有很强的逻辑性，求解方法开放、灵活，是考查学生的理性思维、逻辑推理和化归能力的好素材。纵观近几年全国各地的高考试题，不难发现求某些形式较为简单的递推数列问题更是近年来的高考热点之一。普通高中《数学课程标准》指出“能在具体的问题情境中，发现数列的等差关系或等比关系，并能用有关知识解决相应的问题”。可见，让学生运用已有的等差、等比数列知识去解决新的数列问题是课程标准的要求，也是高考“能力立意”的要求，本文对近年的高考题或课本上的习题为例，对几类常见的递推数列求通项问题中的构造法（转化为等差、等比数列）作一些探求，希望对大家有所启发。

一、加常数策略构造等比数列

对形如an+1=pan+q(p≠1,q为常数），则令an+1+λ=p(an+λ)来构造一个新的等比数列，并利用对应项相等求的值，求通项公式。

例1：（2014新课标II卷17题改编）已知数列{an}满足a1=1 ,an+1=3an+1,求数列{an}的通项公式。

简析：解决该试题的关键是化an+1=pan+q为an+1+λ=p(an+λ)的形式，与已知式子相比较得λ，且从而构建数列{an+λ}为首项为a1+λ(a1+λ ≠0)、公比为p的等比数列，先求出an+λ，再求出；

解：由a1=1 ,an+1=3an+1设an+1+λ=3(an+λ)则an+1=3an+2λ与an+1=3an+1比较系数得2λ=1解得是以为首项、3为公比的等比数列。

二、取倒数构造等差数列

形如an+1an=can+1+dan（其中c、d为不等于零的常数）或的递推式，可以用倒数法来构造。如取倒数法得则可转化为等差数列或拆分变换的情形。又如将递推公式递推式，考虑函数倒数关系有则可归为an+1=pan+q型。

例2、已知数列{an}满足a1=1且求a。n

解：由即

所以，数列是首项为公差为的等差数列， 从而

评注：注意观察和分析题目条件的结构特点，对所给的递推关系式进行变形，使与所求数列相关的数列（本例中数列是等差或等比数列后，就能求出通项公式了。

三、除以指数幂构造等差数列

例2：已知数列{an}满足，求数列{an}的通项公式。

解析：两边同除以3n+1，得：

∴是构成首项为1，公差为的等差数列。

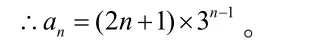
本例中的数列递推公式类型为（其中q、r均为常数(q≠0)，只需先在原递推公式两边同除以qn+1，得：即构造等差数再求出数列（p、q为常数）的递推公式的求数列通项必须用两次构造成等比数列的方法。具体做的通项。

四、用特征根法构造等比数列

对形如法叫特征方程法——其特征方程为若方程两根为则递推公式可构造成如下两种对称形式：，通过分别利用等比知识及加减消元法达到求的目的。

五、取对数构造等比数列或其他特殊数列

对数变换——如将递推公式取对数得，将积、商、幂的形式转化成和、差、倍的形式，从而构成新的等差或等比数列。

对于某些比较复杂的递推式，通过分析结构，联想到与该递推式结构相同或相近的公式、函数，再构造“桥函数”来求出所给的递推数列的通项公式的方法。

总之，递推关系式的数列题，题型多种多样，或直接给出递推关系、或以其他背景出现。要求出数列的通项公式，解决的途径尽管灵活多变，但关键是进行适当变形，将其转换与化归为我们熟知的等差数列或等比数列的通项公式问题，化复杂为简单，化陌生为熟悉，是求通项公式的重要方法，也是高考重点考查的思想。如果我们不能很好地掌握其构造的精髓，在解决这类问题将不可避免地会导致思维混乱、费时和失分。因此我们在教学中应充分重视，加强训练，使学生实现运算能力、推理论证能力水平得到的提升，才能使学生在高考时对相关题型的题境不致发怵，尽快适应。