用轨迹法探求存在性问题*
●张向武 (安阳实验中学 浙江瑞安 325200)
用轨迹法探求存在性问题*
●张向武 (安阳实验中学 浙江瑞安 325200)
随着课改的推进以及教材的修改,点的轨迹内容似乎淡出了初中数学课,但近几年的中考数学压轴题往往都是由动点引发的存在性问题.其实在学生刚学习几何图形时已经知道点动成线、线动成面、面动成体,因此初中阶段不仅要关注培养学生的方程思想,更应培养学生的动点轨迹意识.
轨迹思想;存在性问题;动点
随着课改的推进以及教材的修改,点的轨迹内容似乎淡出了初中数学课,不过在高中阶段的学习中,轨迹思想有着较为重要的作用[1].近几年的中考数学压轴题往往都是由动点引发的存在性问题,它不仅能较综合地考查学生的基础知识、基本技能,更是对学生数学思维能力的一种挑战.学生碰到这类题时如果不得其法,往往会知难而退.面对这样的问题,笔者在教学过程中也常常思考:怎么样才能让学生更好地运用所学知识?不能因为图形在动就不知所措,从而忽略了问题的本质.其实学生刚学习几何图形时已经知道点动成线、线动成面、面动成体,因此笔者认为初中阶段不仅要培养学生的方程思想,更应培养学生的动点轨迹意识.本文主要谈谈如何用轨迹法探求存在性问题,希望对广大师生有所帮助.
1 介绍几种常见的点的轨迹

图1 图2

图3 图4 图5
1)到2个定点距离相等的点(如图1:中垂线);
2)到一个角的2边距离相等的点(如图2:角平分线);
3)到一定直线距离等于定长的点(如图3:2条平行线);
4)到一定点距离等于定长的点(如图4:圆);
5)与2个定点连线的夹角为定值的点(如图5:2条等弧).
2 轨迹法应用举例
2.1 图形存在性问题

图6
例1 如图6,抛物线y=x2-2x-3交x轴于点A,B,交y轴于点C,顶点为D,且点M为对称轴上的一个动点.
1)当△MBD为等腰三角形时,求点M的坐标;
2)当△MAC为直角三角形时,求点M的坐标;
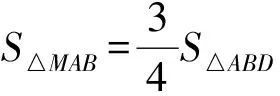
4)当60°≤∠AMB≤90°时,求点M纵坐标的取值范围.
分析 第1)小题考查的是等腰三角形的存在性问题,其中点B,D为2个定点,动点M原有的轨迹是抛物线的对称轴,而要使△MBD为等腰三角形,则需分类讨论如下:当MB=MD时,其轨迹为BD的中垂线;当BD=BM或BD=DM时,其轨迹分别为以点B,D为圆心、BD为半径的圆.综上所述,所有符合要求的点M的轨迹是两圆一线和原有轨迹抛物线对称轴的交点(即图7中的点M1,M2,M3,M4).
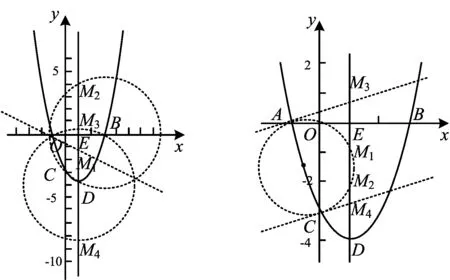
图7 图8
第2)小题考查的是直角三角形的存在性问题,其中点A,C为定点,动点M原有的轨迹是抛物线的对称轴,而要使△MAC为直角三角形,需分类讨论如下:当∠AMC=90°时,其轨迹是以AC为直径的圆;当∠MAC=90°或∠MCA=90°时,其轨迹分别为过点A,C且垂直于AC的直线.综上所述,所有符合要求的点M的轨迹是两线一圆和原有轨迹抛物线对称轴的交点(即图8中的点M1,M2,M3,M4).
第3)小题是附加面积关系的图形存在性问题,其中AB的长度为定值,动点M原有的轨迹是抛物线的对称轴,而要使△MAB的面积为定值,需满足点M到AB的距离为定值,其轨迹为2条平行线,所有符合要求的点M的轨迹是2条平行线和原有轨迹抛物线对称轴的交点(即图9中的点M1,M2,M3,M4).
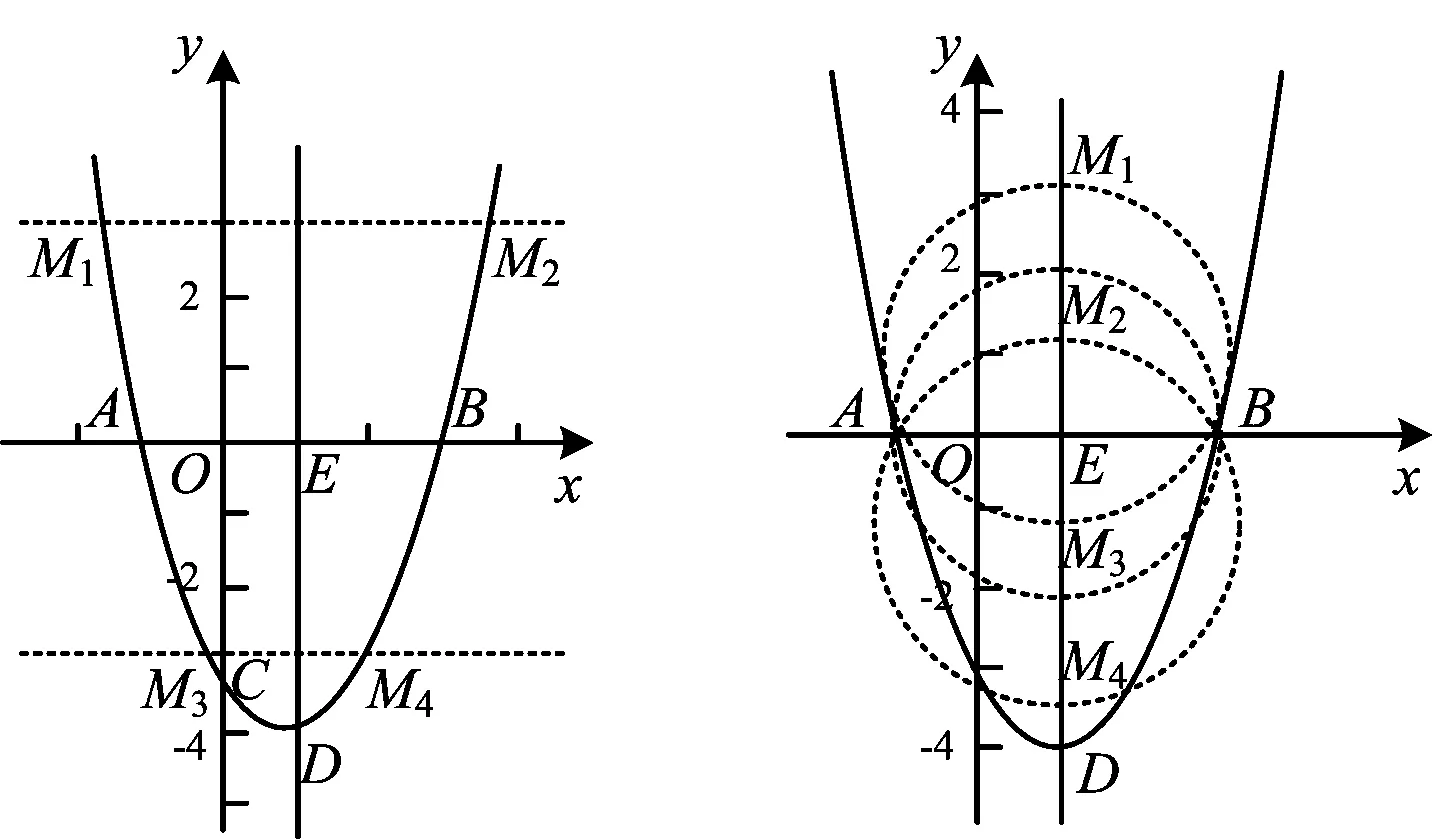
图9 图10
第4)小题是附加特定角的数量关系的图形存在性问题,其中A,B为定点,动点M原有的轨迹是抛物线的对称轴,而要使60°≤∠AMB≤90°,需找到满足M到定点A,B连线的夹角为60°和90°的状态点,其轨迹分别为2条圆弧,符合要求的点M的轨迹是4条圆弧和原有轨迹抛物线对称轴的交点(即图10中的点M1,M2,M3,M4),因此M1M2和M3M4就是点M的运动范围.
2.2 最值存在性问题
例2 如图11,在矩形ABCD中,AB=4,AD=8,E为AD的中点,点P,Q分别是射线AB,BC上的动点,且AP=BQ,线段AQ,EP交于点G,联结CG,则CG的最小值为______.
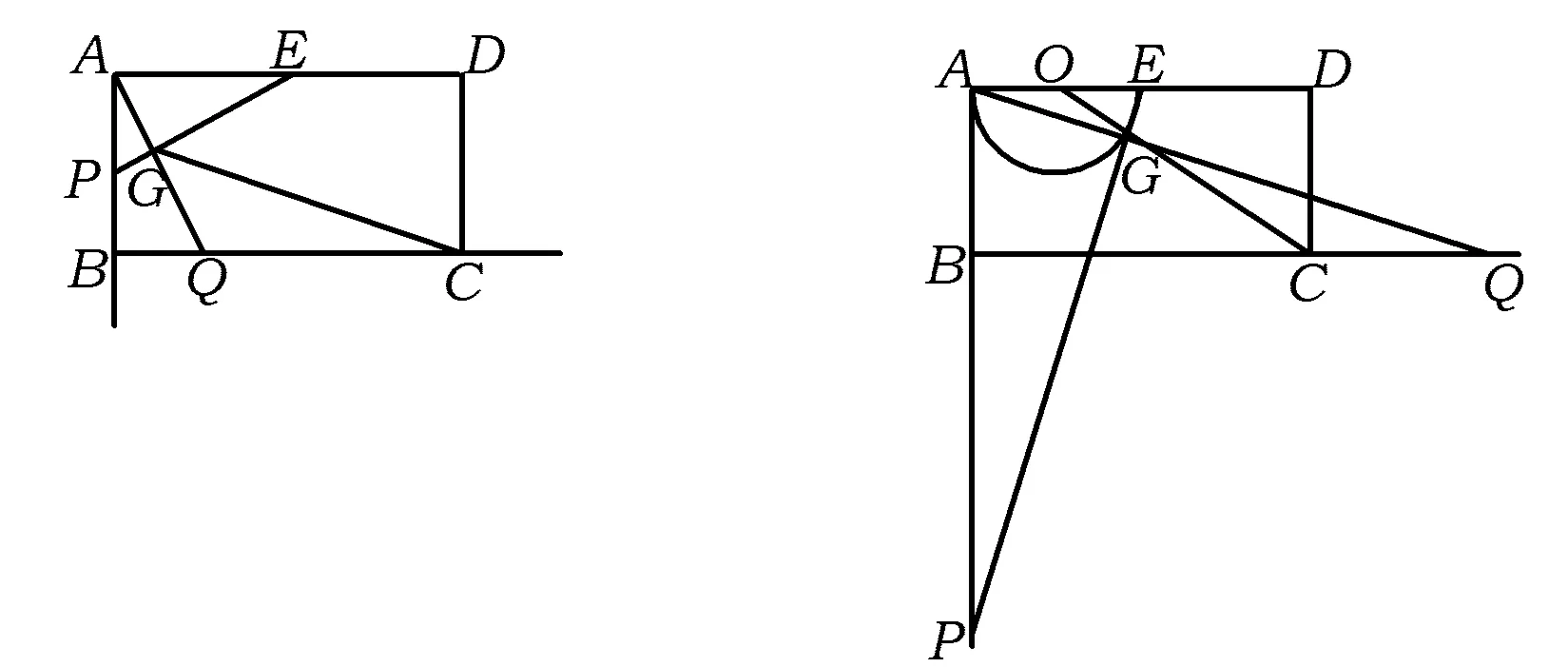
图11 图12
分析 本题是关于动点G到定点C的距离最值问题.首先考虑动点G的运动轨迹是直线还是曲线.分析已知条件可得△ABQ≌△EAP,进一步得到AQ⊥EP;然后运用轨迹思想把问题转化为点G到定点A,E连线的夹角为90°的轨迹上的点和定点C之间距离的最值问题,如图12,当圆心O和点G,C共线时,CG取最小值.
3 中考链接
例3 如图13,抛物线y=ax2+bx+c与x轴交于点A和点B,与y轴交于点C(0,3).
1)求抛物线的解析式.
2)若点M是抛物线在轴下方上的动点,过点M作MN∥y轴交直线BC于点N,求线段MN的最大值.
3)在第2)小题的条件下,当MN取得最大值时,在抛物线的对称轴l上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
(2016年福建省漳州市数学中考试题第24题)
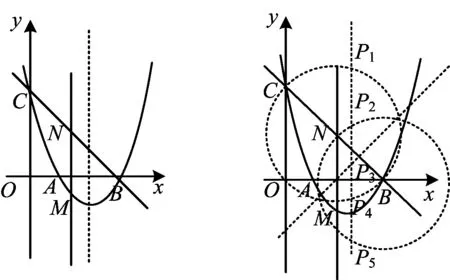
图13 图14
分析 本题的第3)小题同例1第1)小题,通过轨迹法判断满足△PBN是等腰三角形的点P的轨迹是两圆一线(如图14),与对称轴的交点分别为P1,P2,P3,P4,P5.
1)求反比例函数的关系式和点B的坐标.
2)如图16,过BC的中点D作DP∥x轴,交反比例函数图像于点P,联结AP,OP.

图15 图16
①求△AOP的面积;
(2016年山东省济南市数学中考试题第26题)

图17

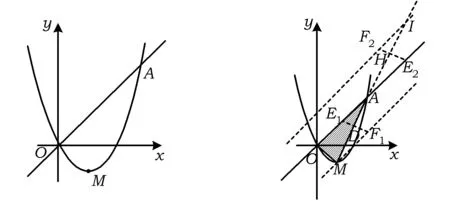
图18 图19
例5 如图18,在平面直角坐标系中,一次函数y=x与二次函数y=x2+bx的图像相交于点O,A,点A(3,3),点M为抛物线的顶点.
1)求二次函数的表达式.

3)问:直线OA上是否存在点E,使得点E关于直线MA的对称点F满足S△AOF=S△AOM?若存在,求出点E的坐标;若不存在,请说明理由.
(2016年江苏省常州市数学中考试题第27题)
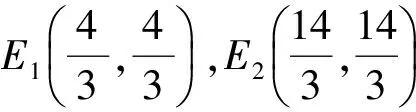

图20 图21
例6 如图20,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,A′的对应点为A.当CA′的长度最小时,CQ的长为
( )
(2016年湖北省鄂州市数学中考试题第10题)
分析 本题同例2,通过轨迹法把问题转化为定点C到以点P为圆心、PA为半径的轨迹⊙P上的动点A′之间的最值问题.如图21,当圆心P和点A′,C共线时,CA′取最小值.故选B.
4 小结
解题是数学学习的一个核心内容和一种最基本的活动形式[2],通过解题活动才能让学生对数学思想方法有所领悟,然后又可以运用其解决一类数学问题.本文列举的动点存在性问题常常由主动点引起随动点,它们相互之间会存在某种依赖关系,从而引起线动和形动,但归根结底是因为点动.如果能注意并弄清关键点的运动轨迹,运用轨迹思想就能准确地化动为静,找到运动中的不变量,最后综合运用数学的相关知识有效解题.
[1] 张克玉.运用轨迹思想 巧解有关问题[J].中学数学教学(数学),2015(6):37-39.
[2] 罗增儒.解题教学引论[M].西安:陕西师范大学出版社,2001.
2017-02-19;
2017-03-21
张向武(1976-),男,浙江瑞安人,中学高级教师.研究方向:数学教育.
O123.1
A
1003-6407(2017)06-38-03

