妙法共欣赏 疑义相与析*——武汉市2017届高三二月调考压轴试题的解法研究

●李红春 (武汉市黄陂区第一中学盘龙校区 湖北武汉 430312)

●孔 峰 (武汉市教育科学研究院 湖北武汉 430022)



妙法共欣赏 疑义相与析*
——武汉市2017届高三二月调考压轴试题的解法研究

●李红春 (武汉市黄陂区第一中学盘龙校区 湖北武汉 430312)

●孔 峰 (武汉市教育科学研究院 湖北武汉 430022)

文章通过对湖北省武汉市2017届高三二月调考压轴试题的解法展示，揭示了不等式放缩的特殊技巧，阐述了抓住“问题间前后联系”和“数学中的基本”来突破解题障碍，同时要注重压轴试题的命题思想．

压轴题；单调性；放缩

湖北省武汉市2017届高三二月调考试卷的导数压轴题，表述简洁，涉及高考中的热点(函数)，蕴含着丰富的数学思想，是一道以能力立意的巧题，其解法思维跳跃性强，具有研究价值，倍受一线教师的关注.笔者通过深入分析，得出了如下方法，供同仁参考．

1 试题及解答

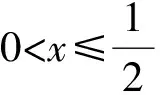
本题第1)小题比较容易，下面重点研究第2)小题的证法：

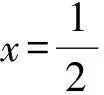
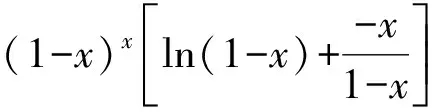
g′(x)=x-x(-xlnx+1-x)-

(1-x)x-1[-(1-x)ln(1-x)+x]≥0.

(1)

而-xlnx+1-x>0，即需证

(2)

(1-x)1-x≥xx,

(3)

(4)

由第1)小题可知

xlnx-(1-x)ln(1-x)≤0,

而2x-1≤0，从而式(4)恒成立.

综合式(3)和式(4)可知式(2)成立，故式(1)得证，从而原不等式得证．

xlnx-(1-x)ln(1-x)≤0，

即

xlnx≤(1-x)ln(1-x)，

亦即

-xlnx≥-(1-x)ln(1-x).

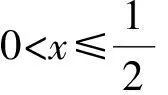
-xlnx+1-x≥-(1-x)ln(1-x)+x>0.

又xlnx≤(1-x)ln(1-x)，得

lnxx≤ln(1-x)1-x，

则

xx≤(1-x)1-x，

从而

x-x≥(1-x)-(1-x)>0，

即x-x(-xlnx+1-x)≥(1-x)x-1[-(1-x)ln(1-x)+x]，

亦即

g′(x)≥0，

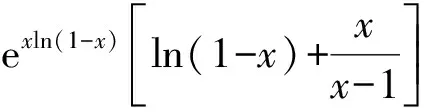
即

(1-x)lnx>xln(1-x).

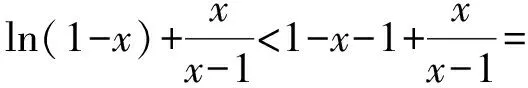
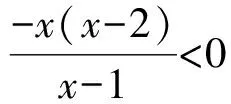
从而

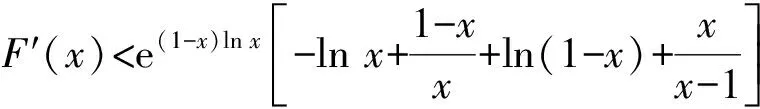
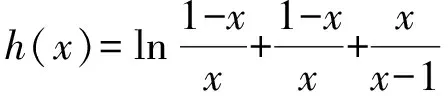
于是

F′(x)<0，

故

由第1)小题知xlnx≤(1-x)ln(1-x)，即

lnxx≤ln(1-x)1-x，

亦即

xx≤(1-x)1-x，

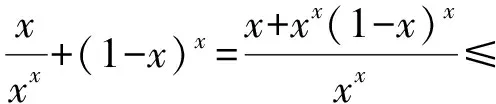
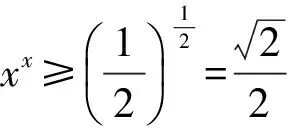
即

2 解题感悟

2.1 解题要注意前后问题的联系

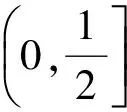
总之，在解题过程中，我们应该反思：通过前面的问题解决，我们能得到什么，要证的问题还需要什么，能否在已知与未知之间寻找联系想办法将问题解决；如果割裂了前后问题之间的联系，也就漠视了命题人设置前面这些基础问题的良苦用心，解题可能迷失方向[1]．

2.2 要注意压轴试题与中档题的区别

面对这道压轴题，很多师生反映极度不适应.其实，压轴试题有其独特的特点，如考查知识点不一定多,但技巧性强,并考查学生的创新思维和综合运用知识的能力,对解题方向性与途径选择的合理性要求要更高[2].

2.3 解题要善于转化

[1] 李红春．两例数列求和不等式证明引发的深刻思考[J]．数学教学研究，2014(9)：44-45．

[2] 李红春．一道联赛试题的多视角求解[J]．中学教研(数学)，2014(4)：46-47．

[3] 李红春．立足函数特征 陈题新掘精彩[J]．数学通讯：上半月，2015(11/12)：2-4．

2017-02-20；

2017-03-21

李红春(1977-)，男，湖北武汉人，中学高级教师．研究方向：数学教育.

O122.3

A

1003-6407(2017)06-21-03