一道学考题的多种解法*

●沈建刚 (萧山中学 浙江杭州 311201)



一道学考题的多种解法*

●沈建刚 (萧山中学 浙江杭州 311201)

浙江省2016年4月的高中数学学考卷第18题，函数式中含分式、绝对值，并带2个参数，同时又复合了“恒成立”与“存在性成立”等不等式问题，是一个考查点丰富、逻辑性要求较高的难题.在解答过程中，笔者发现，该题解法多样、灵活、多变，值得师生认真研究．

学考;恒成立;复合最值

( )

C.(-∞,1] D.(-∞,2]

(浙江省2016年4月高中数学学考卷第18题)

本题中函数式含分式、绝对值，并带2个参数，同时又复合了“恒成立”与“存在性成立”等问题，是一个考查点丰富、逻辑性要求较高的难题.它将中学数学中的函数与不等式问题提到了一定高度.在解答过程中，笔者发现，该题解法多样，各种解法又都围绕高中数学的难点知识，处理方式灵活、多变，这样的题值得师生认真研究．

分析1 这是一个“恒成立问题”与“存在性成立问题”的复合题，分2个层面处理.先处理内层：“存在x0∈[1,2]，使得f(x0)≥m”，即f(x)max≥m;再处理外层：“对任意的正实数a和实数b，使f(x)max≥m”，这是关于2个参数的恒成立问题，利用逐一解决的办法，先b恒成立，再a恒成立，若设f(x)max=h(a,b)，即先求h(a,b)关于b的最小值，进一步求关于a的最小值t，则m≤t.

g(x)∈[g(2),g(1)]，

即

g(x)∈[1-2a-b,2-a-b]，于是f(x)max=|g(x)|max=max{|1-2a-b|,|2-a-b|}.设max{|1-2a-b|,|2-a-b|}=h(a,b)，下求h(a,b)关于b的最小值.因为

|1-2a-b|+|2-a-b|≥

|(1-2a-b)-(2-a-b)|=1+a，

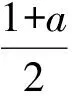
图1 图2

解法3g(x)∈[1-2a-b,2-a-b]，将它画到数轴上，如图2所示，g(x)表示的是一个区间，区间长度为1+a，当b变化时，区间在数值上左右移动，但长度不变.因为

分析2 上述3种解法对绝对值的处理方法是一致的，都用到“因为f(x)=|g(x)|，所以f(x)的最大值在g(x)取最大或最小时取到”.也可作下面的处理：|g(x0)|≥m，即g(x0)≥m或g(x0)≤-m，可形成下列2种新的解法：

解法4 存在x0,使得|g(x0)|≥m，即

g(x0)≥m或g(x0)≤-m，

等价于g(x)max≥m或g(x)min≤-m,即

g(1)=2-a-b≥m或g(2)=1-2a-b≤-m，

变形为

b≤2-a-m或b≥1-2a+m.

图3

由题意，上述2个不等式对于任意的实数b成立，如图3所示，则必须让2个不等式解集的并集为R，从而

1-2a+m≤2-a-m，

解法5 由解法4可知

g(1)=2-a-b≥m或g(2)=1-2a-b≤-m，

可化成

a+b≤2-m或2a+1≥1+m.

若将a理解为横坐标，b理解为纵坐标，上述不等式包含的区域记为A，将条件a>0,b∈R表示的区域记为B(实际即y轴的右边部分),由题意知必须满足B⊆A(小范围推出大范围).

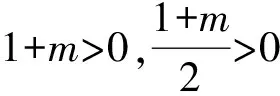
图4 图5 图6

以上解法均围绕问题的难点，作了灵活、多变的处理：

1)绝对值的处理，如解法1～3，避开了对绝对值函数翻折的考查，利用绝对值函数的最大值取决于绝对值里面函数的最大值(或最小值)的特征，转化为考查里面函数的最值.解法4与解法5利用“|x|≥a”与“x≥a或x≤-a”的等价性，解法6利用|f(x)-g(x)|表示“2个函数值的距离”的几何特征.

2)多层分类讨论的处理，如在解法1中，得到绝对值里面函数的最大值与最小值，接下来要解决的问题是2个函数取绝对值后谁大？按部就班的讨论会非常复杂，而且找到了最大值后又进一步要求最小值.解法1～3的处理方法是“2个事情一起做了”，就如电脑打“词语”，有时直接打“词语”比逐字打要方便，3种解法均展示了复合最值“最大求最小”的处理方法.实际上在解法1中，若|1-2a-b|+|2-a-b|≥|(1-2a-b)-(2-a-b)|=1+a>1，则可更直接得到答案，它将“a,b”恒成立“一起做了”.这或许是简化分类讨论题的方法之一．

3)存在性成立与恒成立的处理，除了转化为最值处理外，在解法4中，将“对于任意的b恒有b≤2-a-m或b≥1-2a+m”转化为不等式“x≤2-a-m与x≥1-2a+m”解集的并集为R”，即将逻辑关系转化为集合包含关系.这是一种新颖的处理方式，解法5也是如此．

在一个问题的解决中，调用了众多知识，采用了各种方法，并且这些方法差异较大，这是不多见的.笔者认为这是一个“好”题，值得研究.笔者只是抛砖引玉，希望得到更多读者的关注，会有更多奇思妙想，期待出现“一览众山小”的解法与观点．

2017-04-10；

2017-05-10

沈建刚(1970-)，男，中学高级教师．研究方向：数学教育.

O122.1

A

1003-6407(2017)06-封三-02