课堂教学因探究而精彩*——双曲线及其标准方程的教学实践与思考

●何淑龙 (真光中学 广东广州 510380)



课堂教学因探究而精彩*
——双曲线及其标准方程的教学实践与思考

●何淑龙 (真光中学 广东广州 510380)

文章通过一节课的教学设计，说明课堂上如何开展探究性教学：创设情境，激发探究欲望；实验探究，生成概念；辨析对比，深化概念探究；类比探究，推导关键知识；应用探究，深化理解知识,同时阐述了对课堂进行探究性教学设计的思考.

实验探究；类比探究；变式探究；教学思考

1 教学背景

最近，笔者回想起2015年1月在重庆市九龙坡区参加的由中国教育科学研究院举办的“第3届实验区高质量课堂展示活动暨实验区联席会议”.当时，笔者在重庆市铁路中学主讲了一节公开课，课题是“双曲线及其标准方程”.因为本节课的教学内容很常规，学习难度不大，学生容易理解与接受，但要在如此普通的课中创新出彩，得到专家、同行的认同确实有很大的难度.

为了上好这节课，笔者进行了认真地学习与研究.首先分析了学情：重庆市铁路中学是重庆市重点中学，学生素质较高，为开展探究性教学提供了有利条件；其次研究了教材和课程标准：此内容是学生学习了椭圆之后学习的另一种圆锥曲线，椭圆的研究内容与方法为双曲线的学习作了铺垫，学习方法可以迁移，为学生开展探究性学习提供了参考.最终笔者确立了“以学生探究为主的教学设计方案”，并在课堂上让学生充分探究，笔者最终获得了讲课比赛一等奖

为什么这样设计呢？教学效果如何呢？且看下面笔者的教学实践与思考.

2 教学实践

2.1 创设情境，激发探究欲望

探究式教学顺利开展的前提条件是激发学生探究的欲望.如何激发学生的探究欲望呢？方法之一是设计合适的问题情境，引发学生的认知冲突，从而达到激发其探究欲望的目的[1].为此，笔者通过对椭圆知识的复习回顾，引出新的问题，以问题引发学生的认知冲突，激发其探究的欲望.

教学片断1

师：今天有幸来到重庆市铁路中学，首先参观了美丽的校园，了解到学校的光辉历史，老师为同学们有这么好的学习环境、学习氛围而感到骄傲.当参观运动场时，老师不自觉地联想到我们已学过的数学知识——椭圆，请同学们回忆一下我们已学过椭圆的哪些知识？

生1：椭圆的定义、标准方程、几何性质.

师：生1回答得很好，那么椭圆的定义是什么呢？

生2：到2个定点的距离之和为定长的点的轨迹叫椭圆.

生3：不对，需要条件：在平面内，即在平面内到2个定点的距离之和为定长的点的轨迹叫椭圆.

生4：还不完美，还需要条件，定长大于2个定点之间的距离.

师：不错，为刚刚发言的几位同学点赞.经过这几位同学的补充，我们得到了椭圆的定义：在平面内，到2个定点距离之和为定长(记作2a，大于2个定点之间的距离)的点的轨迹叫做椭圆.这2个定点叫做椭圆的焦点，记作F1,F2，这2个定点之间的距离|F1F2|=2c叫做焦距.当2a>2c时，轨迹是椭圆，那么2a=2c，2a<2c所对应的点的轨迹是什么呢？

生5：当2a=2c时，点的轨迹为线段F1F2；当2a<2c时，点的轨迹不存在.

师：非常好，同学们对椭圆定义掌握得非常好.是否有同学会思考如下问题：在平面内，到2个定点距离之和为定长(大于2个定点之间的距离)的点的轨迹叫椭圆，那么到2个定点距离之差为定长的点的轨迹是什么呢？

教学感悟 由于是异地上课，“怎样让学生接纳教师”是摆在笔者面前的一个问题.自然亲切的开场白，拉近了与学生的距离；对椭圆相关概念的复习，为双曲线的学习作了铺垫，同时类比导出了新的问题，引起学生的注意与思考，从而激发学生的求知欲望.

2.2 实验探究，抽象生成概念

探究性活动的顺利开展需要好的素材，提供合适的材料是实现探究活动的重要保障.从认知心理学的角度看，学习材料被视为一种信息载体，合适的学习材料能较好地吸引学生自主参与，有利于学习过程的动态生成，是学生思维活动的源泉.那么，提供什么样的材料才能解决引发学生认知冲突的问题呢？笔者从做实验开始，通过分析实验的条件与结论，引导学生归纳总结出双曲线的定义.

教学片断2

师：现在请2位同学到讲台上做2个实验，请同学们观察并思考“由实验的条件能得出什么结论”？

实验1 如图1，取一条拉链，拉开它的一部分，在拉开的2条边上选择其中一边用剪刀剪断，再拉开它的一部分，将2边的端点分别固定在点F1,F2上:把笔尖放在点M处，把拉链逐渐拉开或者闭拢，笔尖所经过的点就画出一条曲线.

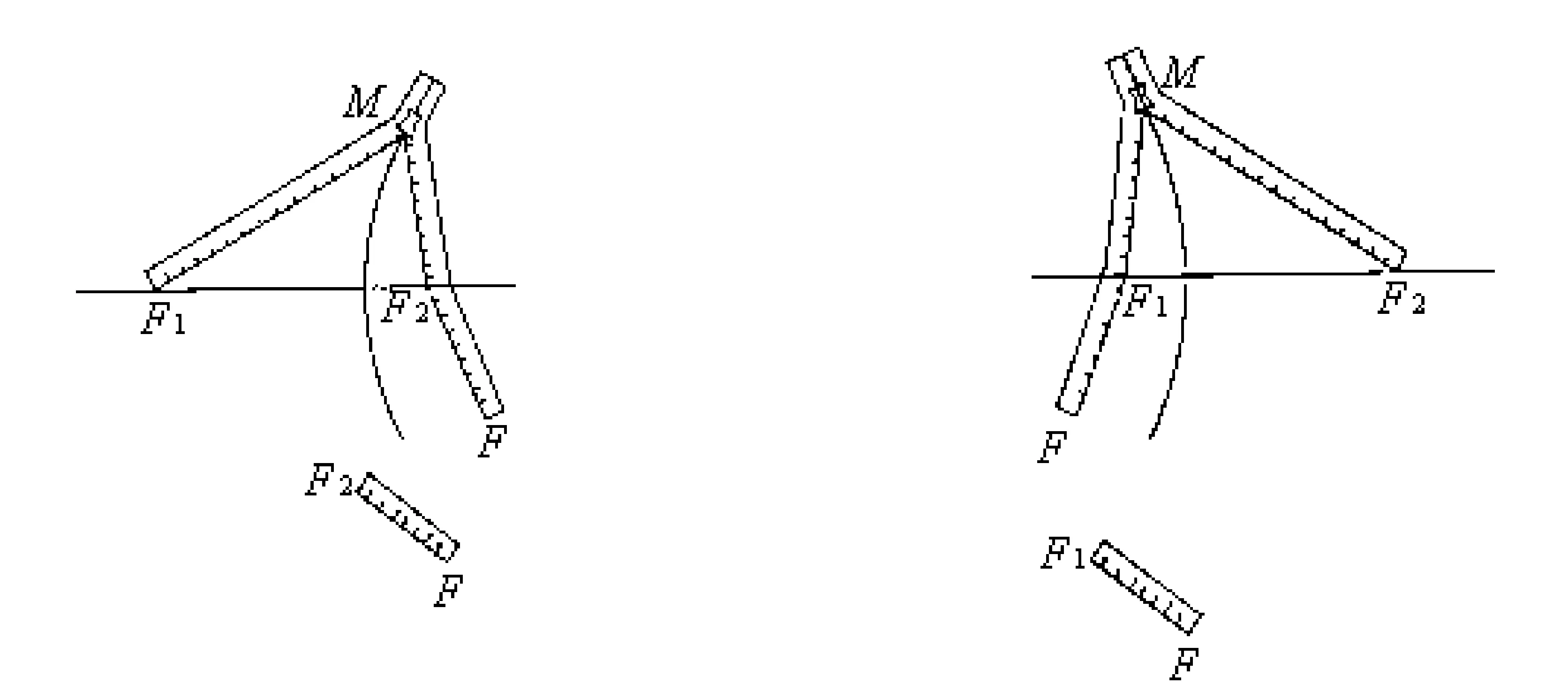
图1 图2

实验2 如图2，将实验1中的拉链调换一下位置，重新操作一次，笔尖经过的点又画出一条曲线.

师：请同学们观察这2个实验，分析一下实验的条件如何，能得出什么结论？

生6：实验1中的条件是F1,F2为2个定点，实验2也是如此.

生7：实验1还有条件|MF1|-|MF2|=|F2F|，实验2的条件是|MF2|-|MF1|=|F1F|.

生8：在实验1中，既然|F2F|剪断了，则|F2F|可看作是常数；|MF1|-|MF2|=常数，F1,F2是定点，笔尖经过的轨迹是一条曲线.

师：生8所说的一条曲线，我们称它为双曲线的一支，能给它下个定义吗？

生9：到2个定点距离之差为常数的点的轨迹是双曲线的一支.

生10：将实验1和实验2结合起来，可得出到2个定点距离之差的绝对值为常数的点的轨迹是2支双曲线.

师：2支双曲线合起来，我们称之为双曲线，刚才同学们说得非常好.类比椭圆的定义,能对双曲线做一下总结吗？

生11：在平面内，到2个定点距离之差的绝对值为常数的点的轨迹叫双曲线.

师：非常好，双曲线是这样定义的：在平面内与2个定点的距离之差的绝对值等于常数(小于2个定点之间的距离)的点的轨迹叫双曲线；这2个定点叫双曲线的焦点，2个焦点的距离叫双曲线的焦距，其符号语言为||MF1|-|MF2||=2a(其中2a为常数，且2a<|F1F2|).

教学感悟 让学生动手做拉链实验，使学生体验到数学知识来源于实践，是从实践中抽象概括出来的.让学生分析实验条件与结论，引导学生总结归纳双曲线的定义.尽管学生的概括归纳可能不完美，但随着交流、探讨的深入，学生们能逐渐完善地给出了双曲线的定义.在教学过程中，教师始终将机会让给学生，让学生做，让学生说，让学生评，让学生体验[2].

2.3 辨析对比，深化概念探究

探究导向可建立新旧知识的联系，是实现理解性探究活动的关键所在.理解就是把新知识点吸纳、融合到已有的知识体系之中.为了深化对双曲线定义的理解，需要类比椭圆，然后对双曲线定义的条件进行辨析.

教学片断3

师：在平面内，点M满足||MF1|-|MF2||=2a(其中2a为常数，F1,F2为定点)，其轨迹一定是双曲线吗？为什么要加上“小于2个定点之间的距离”？

生12：当常数2a<|F1F2|时，点M的轨迹是双曲线；当常数2a=|F1F2|时，点M的轨迹是2条射线；当常数2a>|F1F2|时，点M不存在.

师：为什么呢？

生12：根据三角形的性质“两边之和大于第三边，两边之差小于第三边”.

师：若在平面内点M满足|MF1|-|MF2|=2a(其中2a为常数，且2a<|F1F2|)，其轨迹是什么呢？

生13：还是双曲线.

生14：点M到F1的距离比到F2的距离长，其轨迹是双曲线的一支(右支).

师：同学们回答得很好.利用定义时，我们要注意双曲线的条件，特别是与椭圆的对比时，不能生搬硬套.

教学感悟 通过问题导学，类比椭圆的学习，让学生去辨析双曲线的概念.在辨析中学生对双曲线概念的理解更深刻、更全面，在整个教学过程中，教师重在“导”，而学生多在讨论、交流、争辩.

2.4 类比探究，推导方程

把握学生探究活动的起点，营造独立探究的机会，是实现探究活动的重要基础.认知理论认为：理解是新信息与原有知识经验相互作用的过程.要使新旧知识能相互作用、发生联系，前提是帮助学生准备好已有的认知结构[3].由于学生已经学习了椭圆方程的推导，推导双曲线的方程可让学生独立思考、自主探索和推导，然后相互交流.

教学片断4

图3

师：我们刚刚学习了双曲线的定义，能否根据定义推出双曲线的方程呢？请同学们独立思考并推导，有问题可与同桌合作.

(10分钟后，教师展示学生的成果.)

生15(投影)：建立如图3所示的坐标系，其中F1(-c,0)，F2(c,0).由||MF1|-|MF2||=2a(其中2a<2c),设M(x,y)，可知

2边平方得

(x+c)2+y2+(x-c)2+y2-

师：生15做到此就做不下去了,有同学能继续吗？

生16：生15根据求轨迹的方法建系、设点、列式，都做得很好，但化简方面做得不好，太繁了，以致于做不下去.我认为只要计算能力足够强，还是能做下去的.

师：生16分析得非常好，我们看看下一位同学做得怎么样？

生17：建立如图3所示的坐标系，F1(-c,0),F2(c,0),由||MF1|-|MF2||=2a(其中2a<2c)，设M(x,y),则

即

亦即

再2边平方，整理得

(c2-a2)x2-a2y2=a2(c2-a2).

师：非常好，若上式2边同时除以a2(a2-c2)，则

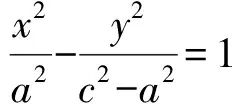
这样的结构是不是非常简洁呢？接下去该如何做？

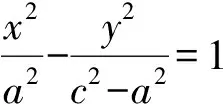
师：生17做得如何，能给出评价吗？

生18：生17做得很好，像推导椭圆方程一样，移项平方，2边可消去很多项，再移项平方，就得出了结果.

师：还有别的推导方法吗？

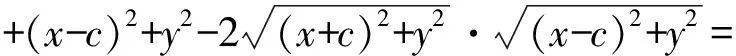
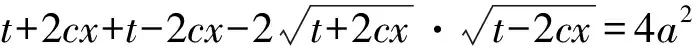
化简得

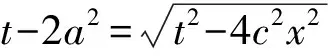
2边平方得

a2t-c2x2=a4,

于是

a2(x2+y2+c2)-c2x2=a4,

化简得 (c2-a2)x2-a2y2=a2(c2-a2),

即

师：生19做得非常棒，具有很强的创新能力和观察分析问题的能力，我们为他的创新鼓掌.

(学生纷纷鼓掌庆贺,课堂气氛活跃起来.)

师：若焦点在y轴上，双曲线的标准方程是什么呢？请说明理由.

教学感悟 考虑到学生在学习椭圆时曾经推导过椭圆的标准方程.教师相信，学生通过类比椭圆的学习可自行推导双曲线的标准方程，因此放手让学生推导，并展示其成果.对其中不太好的做法，也是引导学生找出其闪光点，并分析失败的原因，使学生感到有信心和希望.对其中好的做法，加以肯定，展示其成功之处，使学生体验到成功的喜悦.没想到教学时还有学生想到创新的做法，令师生大开眼界.教学时，教师应把时间还给学生，让学生独立思考、合作交流、相互评价.

2.5 变式探究，提升能力

采用变式探究是实现探究活动的重要举措.变式探究有助于学生深化知识、完善知识结构、理清知识的来龙去脉.在运用双曲线的定义和方程解题时可考虑采用变式探究，以深化知识的理解，提升学生的能力.

教学片断5

师：刚才学习了双曲线的定义及标准方程，现在我们来应用所学知识解决问题.

问题1 已知双曲线的2个焦点坐标为F1(-5,0)，F2(5,0),双曲线上一点P到F1,F2的距离之差的绝对值等于8，求双曲线的标准方程.

b2=c2-a2=9,

师：生21做得非常好，若将题目变为：在平面内，P(x,y)满足

则点P的轨迹方程是什么？

师：非常好，理解得很深刻.还能编写一些题目吗？

生24：已知双曲线的焦点坐标为F1(0,-5)，F2(0,5),双曲线上一点P到F1,F2的距离之差等于8，求双曲线的标准方程.

生25：若点P(x,y)满足

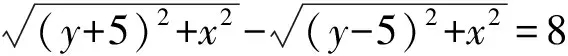
则点P的轨迹方程是什么？

生26：若点P(x,y)满足

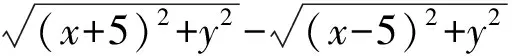
则点P的轨迹方程是什么？

师：非常好，刚才同学们编写的都是用定义求双曲线标准方程的问题.

教学感悟 应用所学知识解决问题是学生巩固知识、深化理解知识的必要环节.教学时教师从一道简单题进行变式，让学生理解与领悟双曲线定义的不同表述，并让学生自己编题训练，使学生真正理解所学知识，也许学生的编题不成熟，有些是模仿的，但学生的自主学习能力得到了提升.

3 教学思考

本节课的教学，教师放手让学生自主活动、自主探究，把时间还给学生，把机会让给学生，学生兴趣浓厚，思维积极，课后也得到了大多数听课教师的好评.通过这节课的教学，笔者有如下思考：

1)这节课为什么要进行探究性教学，让学生自主探究呢？

从学习内容说，学生不是第1次学习圆锥曲线，前面已学习过椭圆.双曲线与椭圆有很多相似之处，学生只需类比、对比即可，而类比、对比的思想方法在高中数学中经常用到.

从教学重、难点看，重点是双曲线定义及其辨析，难点是双曲线标准方程的推导.在突出重点的过程中，与椭圆类比，先做实验，让学生观察思考，分析实验条件与结果.类比椭圆得出定义，用拉链动手实验，而不是电脑操作实验，给了学生更多的时间与空间.从难点的突破方面看，推导双曲线的方程与椭圆方程的推导是类似的，只不过多了绝对值，对学生来说增加了难度.从学生生源来看，学生的素质高、自主学习能力强，为实现探究性教学奠定了基础.事实上只要给学生充足的时间，让学生合作，学生的探究工作就能做得非常好.

2)教学如何实现“探究式教学”？

实现探究式教学，要根据教学内容与学生实际.若教学内容太难，学生无法达到的，则不能采用，如等比数列求和公式的推导就不能用此法.实施探究式教学，教师要做到“敢降”“敢放”“敢等”.“敢降”即是教师要“降低”自己的“教师身份”与学生“平起平坐”，把问题设计得平易近人，降低问题的起点，让学生参与进来；“敢放”就是教师要有收放自如的底气与能力，创设情境开放，让学生大胆地提出自己的思路，让学生有充分的时间去思考与探究，把表现的机会让给学生；“敢等”是教师的一种气质，就是教师要有把握时机的耐心与从容，耐心地等待学生解决问题.

本节课的教学内容非常适合探究性教学.在教学中笔者原先“不敢降”“不敢放”“不敢等”，但是有听课师生的鼓励与支持，就大胆地进行了尝试，事实上效果还是不错的.

[1] 林婷.突出主体地位 追寻高效复习[J].数学通讯，2013(3)：47-51.

[2] 金明.课堂教学应让学生尽情地“说”[J].中学数学，2013(5)：9-12.

[3] 何淑龙，金明.解题教学应探寻解题思路之源——从一道考题谈数列不等式的证明策略[J].中学数学研究，2013(2)：34-36.

2017-02-11；

2017-03-13

2016广州市教育规划课题(1201574155)；广东省“十二五”规划课题(2013YQJK080)

何淑龙(1976-)，男，湖南祁阳人，中学一级教师.研究方向：数学教育.

O123.1

A

1003-6407(2017)06-06-05