数形结合思想在高中数学教学中的应用分析
黎彦峰
摘 要:数学本质上是围绕着“数”与“形”两大元素来不断发展和演变的,因此“数”与“形”之间的关系和转化是数学教学重点内容,教师应予以重视,本文从数形结合思想的优势入手,简要介绍数形结合思想在高中数学教学中的应用。
关键词:数形结合 高中数学 教学
在现代数学中有四大重要的思想方法,分别为:数形结合思想、函数与方程思想、分类讨论思想及转化与化归思想[1]。数学学科之中,“数”与“形”是密不可分的,二者在相互融合的基础之上又能够互相转化,因此,数学教师应将数形结合思想引入到高中数学教学之中,从而将复杂的数学问题简单化处理,提升学生的解题效率。
一、数形结合思想的优势
1.为学生提供新的解题思路
传统数学教学过分看中结果,而忽略了学生的解题思路,为了改善学生解题困难这一局面,应将数形结合思想引入到高中数学教学之中,通过数形结合训练,使学生能够初步产生“数”与“形”的认识[2],将数学教学影响提升到学生分析层面,学生利用“数”与“形”的转换,了解新的解题思路,一改以往重结果轻过程的教学方法,进一步提升高中数学教学水平。
2.培养学生数学思维水平
高中数学的难度较大,具备极高的抽象性和逻辑性,学生难免会出现学习困难,利用数形结合方式来开展教学,使学生产生数形结合意识,将抽象性、逻辑性高的数学概念和数据向具象化转换[3],从而提高学生的学习兴趣,使数学教学进展更为顺利。另一方面,数形结合思想能够将高中数学进行贯穿,帮助学生形成统一、全面的数学知识体系。在学生遇到数学难题时,通过传统方法很难进行解题,而将数学与图形相互转换,利用逆向思维来进行解题,对学生的数学思维水平培养具有积极影响。
3.提升学生数形转换能力
数形结合能够充分揭露数学的本质,在高中数学之中引入數形结合思想,能够帮助学生将数学概念、定理、推论从感性认识上升到理性认识,从而帮助学生对数学知识加以深刻理解,培养学生的数学观察能力、归化能力。高中阶段数学学习中,几何占有很大部分,在学生学习几何知识时,将数学解题思想深入到其中,为学生几何解题提供新的思路,通过这种方式令学生不断从“形”转化为“数”,再从“数”转化为“形”,能够有效提升学生的数形转换能力,从而加深学生对数学解题过程的认知。
二、数形结合思想在高中数学教学中的应用
1.数形结合思想在高中集合与函数教学中的应用
在高中集合教学引入数形结合思想能够提升学生的认知能力,利用韦恩图以及数轴等图形元素,使学生能够直观的了解不同集合之间的关系[4],从而更好的判断集合客观情况,有利于学生开展相应的运算。函数方面更需要借助图形来进行计算,利用图形和函数解析式,从而迅速找到解题方法。例如,某学校有美术、舞蹈、乐器3个第二课堂兴趣小组,3个小组分别有30、27、22名学生,一些学生参加了不止一个兴趣小组,参加美术和舞蹈小组有6人,参加乐器和美术小组有4人,同时参加三个小组的有3人。问只参加两个小组的学生有几名?这一问题中数据信息较多,刚刚接触集合的学生很难直观了解各个集合关系,造成解题困难,为了改变这一局面,教师可将韦恩图引入到教学之中,利用数形结合的思想来开展教学,使得学生能够直观了解到数据信息之间的关系,从而获得更好的解题思路,经过计算:参加舞蹈和乐器小组的学生有:22-10-4-3=5(人),那么只参加两个小组的学生有:4+6+5=14(人)。
2.数形结合思想在高中几何教学中的应用
几何学科本身就是对图形的研究,在数形结合思想下,教师将方程式与图形之间的关系,引导学生研究方程中的“数”得到几何“图”的性质[5],利用数形结合思想,将方程式与几何图形紧密结合在一起,从而使学生产生几何思维,对学生未来的几何学习产生积极影响。例如,在进行椭圆曲线教学中,为了提升学生的理解效果,教师可利用数形结合来开展椭圆曲线性质教学,先为学生展示椭圆在坐标轴上的图形,并给出椭圆方程:x2/a2+y2/b2=1(a﹥b﹥0),引导学生将这一方程变形,得出:x2=a2(1-y2/b2),所以:x2≤a2,得到:-a≤x≤a,同理可证:-b≤y≤b,综上所述,椭圆曲线在x、y轴的范围分别是:-a与a、-b与b之间,那么可以证明,椭圆曲线是原点中心对称图形。
3.数形结合思想在高中在向量教学中的应用
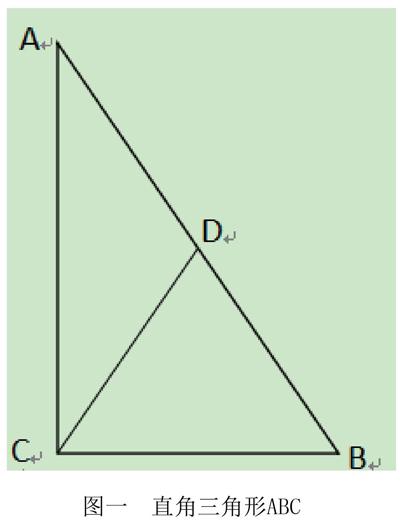
高中数学教学中,向量这一概念尤为重要,向量不仅是代数概念,同时也是几何概念,因此,向量教学中必须应用数形结合思想,利用向量将代数思维与几何思维相互关联,并将代数语言与几何语言相互转换,从而引导学生解决数学实际问题,提升学生的数学解题能力。例如,在证明“直角三角形斜边中线长度与斜边长度相等”这一问题中,教师可以为学生画出直角三角形向量图(如图一),因为点D是三角形斜边AB的中点,因此可知:CD=1/2(CB+CA),利用向量运算可知:CD·CD=1/4(CB+CA)·(CB+CA),经过计算,可以得知:CD2+1/4(CB2+CA2),CD2=1/4AB2,所以:CD=1/2AB,故而证明直角三角形斜边中线长度与斜边长度相等。利用向量的计算特点可以为学生解几何题提供更多思路,从而利用数形结合思想了解决几何问题。
结语
综上所处,在高中数学中引入数形结合思想,能够将抽象的代数概念和公式与形象的结合图形相互联系,从而为学生提供新的解题思路,这种方式是数学教学发展的必然趋势,教师应当重视数形结合的重要性,在全面把握教材的基础之上,有针对性的逐步渗透数形结合思想,提升学生的解题能力,从而推动高中数学教育改革深化落实。
参考文献
[1]王英.数形结合思想在高中数学教学中的应用[J].高考,2015(1):135-135.
[2]杨建珍.浅谈数形结合在高中数学中的应用技巧[J].科学咨询,2016(33):87-87.
[3]孙丽艳.数形结合方法在高中数学教学中的应用[J].中国校外教育(下旬刊),2015(10):127.
[4]武蕾,于志萍.高中数学教学应用数形结合方法的分析[J].中国校外教育(中旬刊),2015(9):9-9.
[5]黄江宁.高中数学对数形结合方法的应用探讨[J].数理化学习(高一二版),2015(12):5,8.

