让转化思想“触手可及”

朱绍敏++董丽君

【摘 要】“转化思想”就是将未知解法或难以解决的问题，通过观察、分析、联想、类比等思维过程，选择恰当的方法进行变换，化归为已知知识范围内已经解决或容易解决的问题方法的数学思想。在教学中，教师重视渗透转化思想，通过不断的转化，把不熟悉、不规范、复杂的问题转化为熟悉、规范、简单的问题，可以帮助学生理清知识结构与脉络，有利于学生理解数学的本质。

【关键词】立体图形 转化思想

在小学数学教材中，各知识点之间的转化随处可见。本文以北师大版教材六年级下册“立体图形的整理与复习”教学为例，来谈复习课中如何让转化思想变得触手可及。

一、动态生成搭建平面与立体图形之间转化的桥梁

（一）看平面图形说出面积与周长的字母公式

生：S长=ab S三=[12]ab C长=2（a+b） C三=a+b+c

（二）引出四种立体图形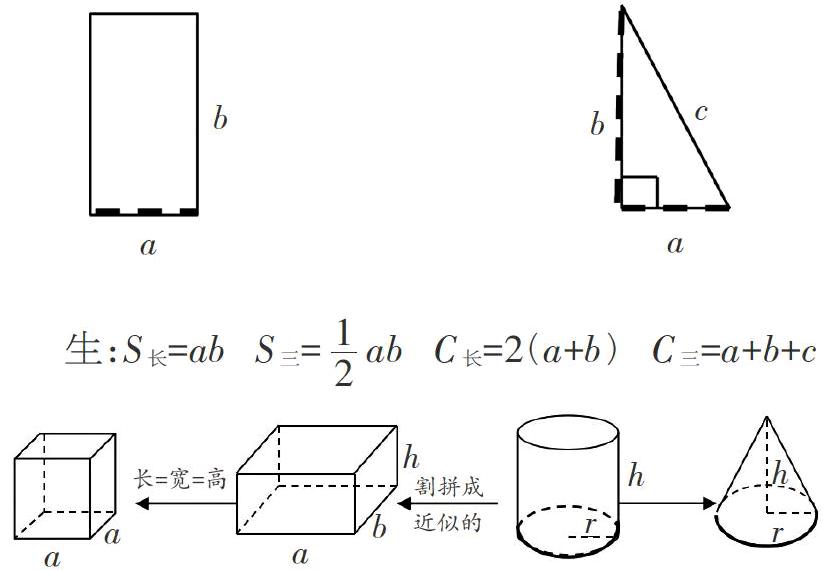

师：分别以长方形的长或宽、三角形的底或高为轴旋转一周，会形成什么图形？

生：形成立体图形圆柱与圆锥。（思考以另外一条边为轴旋转可以产生什么图形）

师：它们的體积分别怎么算？同一个图形沿不同的轴旋转，所得的立体图形体积相同吗？

生：它们的体积与底面积、高有关系。

师：直角三角形如果以斜边c为轴旋转后会形成什么形状呀？

生：它形成的是由一大一小两个圆锥共底面的立体图形，像生活中常见的陀螺那个样子。

师：以前教学圆柱体体积公式时我们是把圆柱转化成什么图形来求体积的？

生：割拼成近似的长方体。

师：当长方体的长、宽、高向三个方向以不同速度缩短或变长时，长、宽、高会出现相等，那么长方体就变成了什么图形？所以说立方体是特殊的长方体。

【评析】由平面到立体过程是一个动态生成的过程，这样设计可以使学生轻而易举地联想起学过的知识，并且进一步理解了这四个图形之间的动态联系，不知不觉渗透了转化的思想，使学生找到知识的源头。并且能够紧紧抓住学生的心理，为后续学习奠定了良好的基础。

二、合作交流展示立体图形计算公式之间的转化联系

（一）体积计算公式之间的转化关系

1.四人小组合作

师：用长方形（正方形）纸巧手折一折，做出上面图形的简单形状或模型。

师：根据上面所给的条件，看模型交流，理一理各图形的特征及运算公式。你可以任选一个图形，也可以多个图形交流。（5分钟）

2.学生代表汇报

生：顶点（8个）、面（6个、形状）、棱（12条、长短），底面（形状）侧面展开形状、公式（表面积、侧面积、体积之间的联系）。

师：同学们想想看，圆锥体积与圆柱体积是在什么关系下推导出来的？

生：等底等高。

师：在这种情况下圆柱体积与圆锥体积之间有什么联系？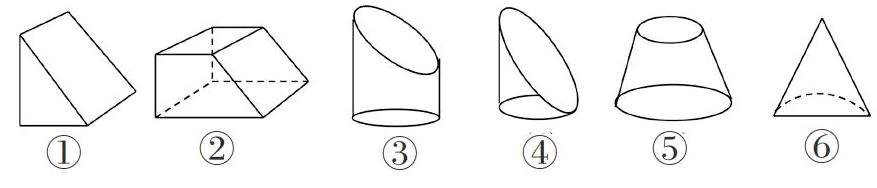

生：圆柱体积是等底等高圆锥体积的3倍，圆锥体积是等底等高圆柱体积的三分之一。

师：（板书：V柱=3V锥，V锥=[13]V柱）它们之间还有什么关系呢？

生：圆柱体积比等底等高圆锥体积大2倍，圆锥体积比等底等高圆柱体积少三分之二。

师：你说得很好，（板书：V柱比V锥大2倍，V锥比V柱少[23]）再观察立方体 、长方体 、圆柱三种图形还发现了什么？它们的体积公式之间有什么联系？

生：它们都可以用一个底面积与对应的高求出图形体积。

师：如果把它翻转一下，现在体积又怎么求呢？

生：原来的底面相当于横截面，原来的高相当于长，还是能够用原来的公式求体积。只不过公式变换了一种说法而已，变成横截面积乘长。

[师板书：V=Sh（横截面积×长），顺势在图上标出底面积阴影部分]

（二）侧面积与表面积计算公式之间的转化关系

师：下面请同学们用手中的纸折一折，折成圆柱体、长方体、正方体空心模型，然后展开并观察三种图形的侧面积与长方形或正方形纸有什么关系。

生：长方体、正方体、圆柱体展开后形状都是长方形或正方形，它们的侧面积就是长方形或正方形的面积。

师：怎么求三种图形的侧面积呢？它们展开图的长与宽与原来三种立体图形有什么紧密联系？

生：原立体图形的底面周长就是展开图的长，原立体图形的高就是展开图的宽。

师：三种立体图形都可以用同一个公式来求侧面积吗？侧面积=底面周长×高。

师：你能同时举几个求侧面积的生活实例吗？

生：铁皮烟囱材料、自来水管材料等，它们两头都是通的。

师：那么它们的表面积有没有联系，是否可以统一为一个公式呢？

生：三种立体图形的表面积都是一个侧面积加上两个底面积求得。

【评析】小组合作交流，能够使学生情绪不过于紧张，而且使组内水平参差不齐的情况得到缓解。能力强的学生在组内起到“传帮带”的作用，能力较弱的学生能够得到组员的指点，获得了表现的机会。通过合作交流与教师的旁敲侧击，学生对圆柱体、长方体、正方体三者之间的关系加深了理解，教师问题的设计由浅入深，随着层层递进的辨析、比较，使三种立体图形的侧面积、表面积、体积公式由“特殊”到“一般”转化，水到渠成，落地有声。

三、创作模型打通部分与整体之间转化的节点

（一）规则变形

师：把圆柱切割成一部分，会变成什么形状呢？能求切割后图形的体积吗？

生：有的还是圆柱，不过变短了，有的变不完整了，怎么求呀？（生疑惑）

师：能创造出原图形的一部分模型吗？用橡皮泥做成正方体或长方体、圆柱体、圆锥体，然后切割出一部分试试。

（师选出典型的模型板演并以学生的名字命名，如付辰煜体）

师：请把切割成的两部分分开与拼接后，组内谈谈这两部分与原来的立体图有什么关系？

生：我知道了！只要拼接一部分上去，使之变成完整的立体图形，然后去掉拼上去的一块体积就能求切割好后的一部分物体的体积了。（很兴奋）

师：现在大家能计算“付辰煜体”的体积了吗？需要哪些条件才能求体积呢？根据学生的要求标上条件或数据。如：r=1cm h=2cm。

生：只要拼上完全一样的一段求出完整的立体图形，然后求一半体积即可。

師：（选出学生典型的模型并在原图上画出相应的图形）有其他计算方法吗？

生：如图①②可以拼上一个完全一样的图形或横截面积乘长的方法求得。

生：图②还可以拼上一小块三角体成长方体。

师：为什么图⑤⑥不能用横截面积乘长计算呢？

生：因为前后形状大小不等，图③可以用半个圆柱加下面一个圆柱的方法计算。

师：我们创造的都是有规则可循的变形，可以通过拼上一个完全一样的图形或一部分图形后“恢复原形”，形成一个规则图形，也能用横截面积×长来计算。

（二）等积变形

师：（掐成一团，不规则麻花状）这样的图形你能求它的体积吗？

生：这像什么呀？是个不规则图形，不是我们学过的图形呀！

师：（笑了笑）什么变了，什么没变？

生：形状变了，变成不规则图形了，但体积没变。

师：对！数学上把这种现象叫等积变形，怎么求等积变形物体的体积？

师请1～2位学生说，结论：V升=V物。

师（投影）：一只底面半径是2厘米的圆柱形玻璃杯里盛了10厘米高的水，现在放进一个不规则的物体（完全浸没在水中），现在水面高度是（ 11 ）厘米？水面上升了（1）厘米？这物体的体积是（ ）立方厘米？ （根据现场实验填上数据）你能求出刚才这个不规则物体的体积吗？

师：如果学生开小差没看见实验过程，你还有什么方法补救吗？（取出物体，在实验中排除物体吸水等一切因素）现在取出物体，水面高度会发生什么变化？高度肯定下降几厘米？水柱下降的体积与物体的体积有什么关系？

生：水柱下降的体积就是物体的体积。

师（板演结论：V物=V降 ）：不管规则或不规则物体我们都能够用这种等积变形的方法，把物体转化成规则的图形来求物体的体积。

【评析】使物体由规则变不规则，再到不规则变规则，是一个辩证思维的过程，本环节分两个层次推进体积的求法。第一层次，通过创作模型、讨论到练习，让学生进一步掌握计算规则部分体积的多种计算方法，也体会了操作讨论对总结方法的帮助。第二层次，利用不规则的等积变形，通过观察、分析、反思，使不规则变规则，计算策略得到了升华。

四、用好板书在书写脉络中体会转化的魅力

师：请同学们静静地看着板书，回顾一下我们这节课的所学。

生：我们学到了用转化法把不规则图形转化成规则图形来计算。

生：我们还学到了圆柱体与长方体和正方体可以相互转化。

生：我们还学到了长方体、正方体、圆柱体都可以用一个体积公式、表面积公式、侧面积公式来求。

师：其实，这一节课我们都是在转化思想的引领下，使各个立体图形之间建立了紧密的联系，知识之间才会融会贯通。

展示板书设计：

【评析】板书设计结构清晰、自然、大方，起到很好得统筹建构的作用，使学生一目了然，培养了学生知识梳理与整理的习惯。

整节课以“转化”的思想为主线，从问题的提炼到全面概括，再到运用转化思想解决更多的问题，层层递进，一气呵成，高年级数学课堂的魅力彰显无遗。同时使“转化”思想立竿见影，触手可及。我们在课堂教学中要不断培养和训练学生自觉的转化意识，将有利于强化学生解决数学问题中的应变能力，从而真正意义上提高思维的深刻性。

（浙江省衢州市龙游县詹家小学 324400

浙江省衢州市龙游县阳光小学 324400）