运用有效策略发展形象思维
孙保华
【摘 要】小学生的数学思维特点,是以数学形象思维为主要形式逐步过渡到以抽象逻辑思维为主要形式,但这种抽象逻辑思维仍然与感性经验直接相联系。这就是说,小学生的思维活动是以形象思维为先导的,而且在进行逻辑思维时,仍然与形象思维密切联系的。对此,在日常教学实践中,教师应通过若干策略来培养学生的数学形象思维。
【关键词】形象思维 教学策略
形象思维不仅有助于学生理解数学知识的形成过程,而且有助于培养学生的空间观念和几何直观能力。因此,在小学阶段要重视学生形象思维的培养,为他们抽象思维的发展打好基础。
小学生的思维特点正处于由形象思维向抽象思维过渡的阶段,在数学学习中形象思维可以起到线索诱导和启发灵感的作用。因此,在教学中我们应运用有效策略,促进学生数学形象思维的发展。
一、挖掘教材,直觀表征
数学中的概念、性质、法则和公式等比较抽象,同时学生在学习中以直观形象思维为主,因此,根据实际教学的需求,我们应充分挖掘教材,尽可能地借助直观表征帮助学生更好地进行数学学习,以提高学生的数学形象思维。
(一)简图
例如,教学两位数乘一位数14×2 的口算时,使学生知道先算2个十得20,再算2个4得8,最后把两次乘积相加得28。在这样的感知活动中,就获得了算法,明确了算理。然后在原式上初步概括,并一边画简图一边引导学生计算:
再通过如上同一形式的几道题的练习,在学生头脑中形成了算法的图式表象,如:
最后概括出两位数乘一位数的口算方法。
(二)表格
表格也是直观表征的方式。一方面,表格可以用于整理信息。例如,苏教版四年级上册中解决买笔记本的实际问题时,出示教材提供的表格,要求学生利用表格整理条件和问题,这样可以使信息和数据更加清晰、直观,能帮助学生更好地分析数量关系。
另一方面,有些实际问题也可以通过列表的方式展现解答的思路和过程。例如,苏教版六年级下册中解决租船的实际问题时,借助列表的直观表征方法帮助学生将不同的方案一一列举出来(如图2),渗透了不重复不遗漏、有序思考的思想,从中一目了然地找到了解决问题的方案。
(三)线段图
线段图是由几条线段组合在一起,用来表示实际问题中的数量关系,帮助我们分析题意从而解答问题的一种平面示意图。借助线段图,可以将信息以及复杂的关系直观呈现,使学生经历从抽象的文字到直观的再创造,学会数学表达,找到解决问题的方法。例如:
总之,这些直观表征对提高学生分析、解决问题的能力,积累解决问题的经验有非常重要的作用。
二、充分感知,积累表象
表象是客观事物经过主体感知以后在头脑中所留下的形象。表象是对过去经历过的东西进行概括的结果,它既以直观的形象反映现实,又具有一定的概括性。表象是形象思维的材料,没有表象的活动就没有形象思维,所以正确、丰富的表象积累,是进行形象思维的基础。
(一)借助演示,积累表象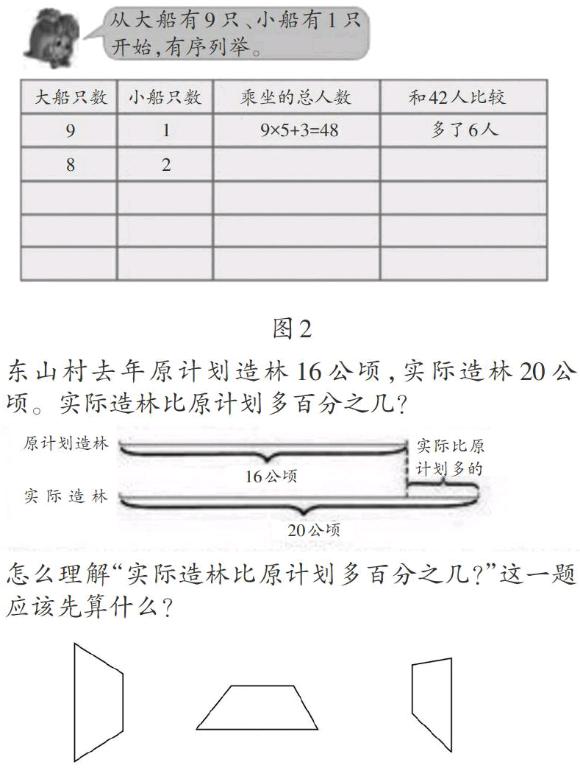
在教学过程中,教师运用图片、实物和信息技术手段辅助教学,把抽象知识形象化,让学生充分观察、比较所学的材料,建立数学概念的表象,增强数学表象的直观性。如认识圆柱体时,可以通过形式多样的圆柱体实物或信息技术手段给学生触摸和观察的机会,建立圆柱体的表象。
(二)引导操作,积累表象
动手操作能使学生多种感官都参与到学习中来,从而在头脑中建立形象,积累表象。如教学平行四边形的面积时,先让学生在硬纸板上画一个平行四边形,再让学生沿着高剪开拼一拼,看一看拼成的图形,帮助学生建立起平行四边形拼成长方形的表象。
(三)指导默想,积累表象
没有形象记忆,就不可能有表象积累。只有让学生将感受到的直观形象在脑子中进行“回忆”,通过默画、默述、默记、默想等手段,才能逐渐强化。如教学体积单位时,教师让学生拿出体积是1立方分米的正方体,通过看一看、摸一摸 、比一比,再让学生闭眼想一想,从而将1立方分米的大小立体地印在了头脑中。
三、数学“直感”,特征判别
在数学学习中,学生对于事物的形象识别,常用带有普遍性的概括表象去对照个别特性的具体形象,并加以判断,是一种整体形象的分解与整合的直观感知过程。这种活动往往不以概念为中介,而一般以原储存在大脑中的表象记忆为对照依据。所以数学直感是在数学表象的基础上对有关数学形象的特征判别。
(一)形象识别“直感”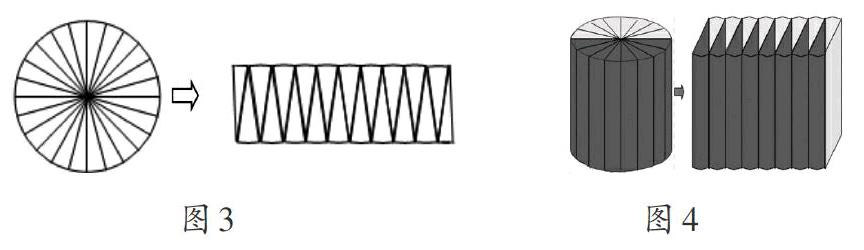
它是用数学表象的特征去比较具体对象以判明该对象是否与有关表象同质。形象识别直感主要表现于各种图形、图式在变式情况下的再认,以及在复合、综合形态下的分解辨认。
例如,指出下图所示图形是不是属于梯形?就是根据已有图形表象进行形象识别。
(二)形象相似“直感”
当形象识别找不到同质的已有表象时,可通过最接近于目标形象的已有表象进行形象识别,比较异同,再作适当的思维加工,找到目标形象与已有表象的联结关节,最后解决问题。
例如,圆柱体体积公式可通过类似圆面积公式的推导方法得出。其形象思维的过程如下:圆面积公式是通过将圆划分成一个个小扇形,再拼成长方形后导出的。通过推导,学生头脑中建立了图形表象(图3)。那么圆柱体体积公式如何推导呢?通过分析,如果把圆看成有一定厚度的圆形,那么就是圆柱体,于是找到了两者的联结关节,圆柱体体积也可以仿照推导圆面积公式的方法求得(图4)。
四、合理想象,激发灵感
爱因斯坦指出:“想象力比知识更重要,想象力是科学研究中的实在因素,是知识进化的源泉。”想象是在头脑中对已有表象经过组合和改造,产生新表象的思维过程。想象是以表象为基础,以直感为手段产生新的表象。因此在教学中要给学生想象的空间和机会,激发其产生靈感。
1.图形想象是以已有的几何图形表象为基础,通过直感对其进行加工和改造,产生新表象的过程。一般认为,图形想象包括图形构想、图形表达、图形识别和图形推理四个层次。如在面临“边长为20米的正方形草地的一角上有根木桩,用绳子拴着一只羊,已知绳长等于正方形边长的一半,求羊吃不到草的草地面积”这样的问题情境时,学生根据情境在头脑中反映出正方形,并对羊能达到的最远的地方进行图形构想,然后进行图形表达,画出相应的草图,完成图形表达进入图形识别。即发现羊能达到的部分是以正方形的顶点为圆心,半径为10米,圆心角为90°的扇形。完成图形识别后便可进入图形推理,即发现羊吃不到草的草地面积为正方形面积与扇形面积的差,至此完成图形推理。
2.图式想象是以已有的图式为基础,通过直感对其进行加工和改造,产生新的表象的过程。图式想象也包括图式构想、图式表达、图式识别和图式推理四个阶段。如对于“李阿姨买了5千克苹果,共花了30元,每千克苹果需要多少元?”这一问题,学生根据问题情境,构想出5千克和30元之间的除法关系,完成图式构想,进入图式表达,即写出算式30÷5。根据图式表达,学生明确是整数除法,完成图式识别进入图式推理,即完成除法计算得出答案。
总之,在数学教学中,我们要依据学生认知心理发展的规律,充分挖掘教材中的素材,让形象进入知识发生、发展的过程,尝试运用多种策略去开拓学生的形象思维能力,强化学生运用形象思维的习惯,有意识地进行形象思维能力的培养。
参考文献:
[1]李光树.小学数学学习论[M].北京:人民教育出版社,2014.
[2]汪绳祖.小学数学教育学[M].北京:高等教育出版社,2000.
[3]张兴华.儿童学习心理与小学数学教学[M].江苏:江苏教育出版社,2011.
[4]陈曦.借助直观表征培养数学思维能力[J].小学数学教育.2016(9).
(江苏省常州市金坛区华城实验小学 213200)

