“交轨法”形式背后的内容

广东广雅中学(510160) 赖淑明

“交轨法”形式背后的内容

广东广雅中学(510160) 赖淑明

本文从两道高考题探究“交轨法”,获得形式背后的本质内容其实是有心曲线的第三定义及第三定义的逆用,借助第三定义逆用的推广拓展交轨法进一步的应用.

交轨法作为求曲线轨迹方程的一种方法被高中的教师和学生所熟识,相信很多老师在讲授这一方法时会很强调交轨法使用的特定形式:求两条过定点的直线的交点的轨迹.强调交轨法使用的关键:两条直线方程相乘,借助曲线方程消参.但是,这一强调并没有起到引起学生重视和提高学生应用“交轨法”的能力.那么,什么是交轨法?顾名思义,交轨法就是求交点的轨迹的一种方法,命名来自于轨迹形成的形式,那“交轨法”形式背后的内容是什么呢?让我们一起从两道高考题研究交轨法的实质.

例1(2010广东高考理数20题)已知双曲线的左、右顶点分别为A1,A2,点P(x1,y1),Q(x1,−y1)是双曲线上不同的两个动点.

(1)求直线A1P与A2Q交点的轨迹E的方程;

(2)从略.

题目分析E是两条动直线的交点的轨迹,这两条动直线都过一个定点和一个动点,定点为已知双曲线的顶点,动点为双曲线上关于x对称的两个点.

解设点M(x,y)是直线A1P与A2Q的交点,因为A1、M、P三点共线,所以

点评交轨法的特点是求两条动直线的交点的轨迹方程,操作形式是相乘消参思考:为什么相乘能消参?

问题分析相乘是为了消参,而本题的参数是点P和点Q的坐标,即x1和y1.而①和②的右边相乘即这不禁让笔者联想到有心曲线的定义,即圆锥曲线的第三定义及其逆用性质.

本质关联1:有心曲线的第三定义

平面内一个动点分别与两个定点的连线的斜率乘积为定值e2−1,当0＜e＜1时,轨迹为去掉两个定点的椭圆.

当e＞1时,轨迹为去掉两个定点的双曲线.

当e=0时,轨迹为去掉两个定点的圆.

本质关联2:有心曲线第三定义的逆用这是双曲线第三定义的逆用.同时,动点E满足

即满足椭圆的第三定义E与两定点A1,A2的斜率的乘积为定值故E的轨迹为椭圆,剔除某些点.由此可见,例1实质上是利用双曲线的第三定义的逆用性质,构造了满足椭圆第三定义的动点轨迹.由双曲线构造椭圆,那么逆向也必然成立,因此,我们可以获得以下变式.

变式1已知椭圆的左、右顶点分别为A1,A2,点P(x1,y1),Q(x1,−y1)是椭圆上不同的两个动点.求直线A1P与A2Q交点的轨迹E的方程.(答案:

2012年辽宁高考题考查的正是变式1

如图,椭圆C0:1(a＞b＞0,a,b为常数),动圆其中b＜t1＜a.点A1,A2分别为C0的左,右顶点,C1与C0相交于A,B,C,D四点.(I)求直线AA1与直线BA2交点M的轨迹方程;(答案:

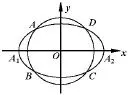
图1

由椭圆构造圆、由双曲线构造圆也成立,如下列变式

变式2已知椭圆的左、右顶点分别为A1,A2,点P(x1,y1),Q(x1,2y1)是椭圆上不同的两个动点.求直线A1P与A2Q交点的轨迹E的方程.(答案:

我们知道有心曲线第三定义的逆用有更一般性的性质:

本质拓展有心曲线第三定义的拓展性质

P(x,y)为圆x2+y2=r2上的动点,A(x1,y1),B(−x1,−y1)为圆的直径的两个端点,则直线PA和PB的斜率乘积为定值−1,即kPA·kPB=−1,其中e2−1=−1.

而2015年广州一模考查的正是这个定义逆用的拓展应用.

(2)求点Q的轨迹方程;

(3)从略.

交轨法形式上是相乘消参,是参数法求轨迹的一种形式.而交轨法应用的实质是有心曲线的第三定义和第三定义的逆用以及第三定义逆用的推广.掌握了交轨法应用这一本质问题也就揭开了交轨法神秘的面纱,就解决了何时使用交轨法,怎样使用交轨法的问题.

[1]刘宗海.交轨法求轨迹到底应该注意什么.数学通讯[J],2005(24): 5-6.

[2]谢鹏作.有心二次曲线的一个性质[J].河北:河北理科教学研究, 2013(5):48-49.

[3]李信任.有心圆锥曲线的第三定义及其在高考中的应用[J].教育教学论坛,2013(10):96-98.