巧用“错误”资源，营造高效课堂

曹素燕

[摘 要] 初中阶段的学生，仍然怀揣着小学时的童真，对待学习不能全身心地投入，尤其是在课堂上，常常会犯下很多的错误. 因此，要想让学生们在课堂上能够聚精会神，营造出高效的学习课堂，教师们就应该从学生的本身出发，去发现学生的问题，引导学生解决问题，方能在成绩上有所突破. 其中，巧用学生们犯下的“错误”，将这种“错误”当作一种资源，反馈给学生们，将是提升课堂品质的有效选择.

[关键词] 初中数学；错误资源；高效课堂

在学生阶段，伴随着自己成长的不仅仅是周围的同学，“错误”也在伴随着我们的成长. 作为学生，出现各种各样的“错误”是十分正常的，也只有学生犯错误了，教师才能发现学生的不足. 但是，在实际的教学中，笔者发现许多教师不知道如何对待学生们的错误. 而笔者认为，教师在遵循“以人为本”教学理念的同时，更应该关注每一位学生的实际情况，让学生正视自己的“错误”，在改错中反思和总结、领悟方法，拓展自己的思维. 也只有教师巧用学生们的这种“错误”资源，使学生正视了自己的“错误”，才能打造一番高效课堂的景象.

巧用“错误”资源，激发学习兴趣

初中生学习中最能够活跃课堂的因素就是兴趣. 因此，在教学的过程中，笔者尊重且理解那些出错的学生，并用学生自己犯下的错误作为教学资源去激发学生的学习兴趣和学习热情，让学生们在错误中积极思考与总结，不断地完善自己.

例如，笔者在课上给学生们出了这样的一道题：某种电脑病毒传播得非常快，如果有一台电脑被感染，那么经过两轮感染后就会有81台电脑被感染. 请学生们用学过的知识分析每轮感染中平均一台电脑会感染几台电脑？倘若病毒得不到有效的控制，3轮感染后，被感染的电脑会不会超过700台？

大部分的学生在做此题时，首先会设在每轮感染中平均一台电脑感染x台电脑，列方程x2=81，然后解出方程. 这时笔者会针对学生的错误解答，让学生们自己去分析解答是否正确，并自由讨论. 当讨论结束后，有学生说“第一轮感染后应该有（x+1）台电脑被感染病毒”时，笔者没有立即评判对错. 在这位学生提出自己的想法时，其余的学生也会自然而然地去活跃自己的思维，去考虑这位学生的叙述. 通过学生间的讨论，他们发现了在第二轮感染之后，新感染的电脑就会有x（x+1）台，同时加上第一轮感染的（x+1）台，就会得出（x+1）2=81，然后解出正确答案. 就这样通过学生们犯下的错误，再一次用错误去引导学生思考，激发他们的学习兴趣和探究欲望.

兴趣是学生们求知的内动力. 笔者在给学生出题目时，让学生们先思考，先自主解答，之后从学生们身上发现普遍存在的错误，利用这样的错误资源，引发学生们学习的兴趣，有了兴趣，学生会主动地探究，有利于高效课堂的形成.

巧用“错误”资源，激发探究欲望

如果说解题是数学的第一阵地，那么“错误”就是数学的第二阵地. 学生在解题过程中必然会出现错题，而这种错题恰恰是一笔巨大的资源，这种资源也只有学生自己才能享受到. 但是往往大多数的学生忽视了这种资源，这就要求教师们要在今后的教学过程中不断地引导，而不是当学生做错时，直接告诉学生正确答案，这样反而会限制学生主动性和创造性思维的发展，只会得到事倍功半的效果. 教师如果对学生们的这些错误进行巧妙利用，将会使学生自主发现错误，从而提高学习的积极性，激发学生们自主探究的学习欲望，日积月累，将培养学生们的探究能力，能得到事半功倍的效果！

例如：在学习“圆”这一节时，笔者给学生设计了这样的一道题：一个钝角三角形，用圆去完全覆盖，怎么样能使得圆最小？

有学生回答最小的圆就是这个钝角三角形的外接圆，而大部分的学生都同意这位学生的说法. 这时候，笔者意识到学生们这样的错误极具代表性，于是为了解决这个问题，笔者反问学生：“难道外接圆就是覆盖住这个钝角三角形的最小圆了吗？”面对问题，学生会对自己刚才的想法产生疑惑. 于是，笔者再让学生自己动手画出这样的圆，看看最小的圆是什么. 然后让学生们互相讨论，总结组内每位学生的观点，并进行反思. 学生们从而否决了自己原先的观点，用假设的方法得出了钝角三角形的最小覆盖圆是以其最长边为直径的圆. 于是全班同学恍然大悟，通过对自己观点的再次研究，重新获得了解题的信心，增强了探究的欲望.

以往的教学中，当学生犯错误时，教师仅仅是直接指出学生的错误. 而在新课改的标准下，教师们应该引导学生合理地面对自己的错题. 教师有效利用学生的错题，因势利导，使得学生发现自己的错误，在初步感受数学思想的同时，学生的思维能力与探究能力得到了极大的提升. 由此可见，巧用“错题”资源，将是打造高效课堂的一把金钥匙！

巧用“错誤”资源，培养发现意识

数学是一门探究性学科，这种探究性要求学生们要具有发现的意识. 学生们要知道，数学的方法、知识以及思想不是单纯地依赖教师的传授，更多的是自己在学习生活中，不断地积累，不断地发现，用自己的发现意识，将别人的东西转化成自己的东西. 在实际的教学过程中，笔者根据每位学生的不同，从每位学生的“错误”入手，挖掘错误中潜在的智力因素，根据学生们的错误提出具有启发性的问题，引导学生在改错的过程中，培养自己的发现意识.

例如，在教学“圆锥的侧面积与全面积”这一节时，笔者给学生设计了这样的一道题：圆锥的底面半径为1，母线长为3，一只蚂蚁要从底面圆周上一点B出发，沿圆锥侧面爬到过母线AB的轴截面上另一母线AC的中点D上，求蚂蚁爬行的最短路程是多少？

在给出这道题时，首先笔者让学生自己独立寻找蚂蚁从B到D爬行的最短路线，学生们思考一番后，认为连接B，D两点即可. 从教师的角度出发，笔者想学生们肯定把平面内“两点之间线段最短”与立体图形中的定义混淆了，于是笔者再次追问学生们蚂蚁真的能从大家规定的路线爬行到D点吗？让学生们再次讨论，笔者告诉学生要仔细读题，既然题目已经规定蚂蚁只能沿圆锥侧面爬行到D点，那么蚂蚁就不能直接从圆锥的内部通过. 当给出这样的点拨，学生们恍然大悟，将圆锥展开成扇形，方能运用“两点之间线段最短”的定义，正确地解出答案. 本题中，笔者就是将学生的“错误”当作一种资源，引导学生们去探究，培养学生的发现意识.

通过本题，相信大家可以看出，学生们很天真地将平面几何的知识与立体几何的知识混为一谈，导致了错误的发生，但是通过笔者在学生思维活动过程中的引导，学生们再次拾起错题，通过探讨发现了错误的原因，然后不断地总结与反思，大大加强了学生们的探究意识. 由此可见，巧用“错误”资源，让学生对所学的知识有了更深的理解，同时也无意间培养了学生的发现意识.

巧用“错误”资源，开展创新思维

学生在解题的过程中，常常因为没有思路而无从下手，导致解题失败. 学生们遇到这样的问题往往是因为自身没有养成良好的思维习惯，再加上没有过多数学思想的支撑，在解题中会遇到瓶颈. 因此，教师在教学的过程中，如果有学生遇到问题，教师就需要适时给予学生点拨，帮助学生们打开思路，并且不断地鼓励. 日积月累，学生们就会突破思维障碍，达到创新的新境界！

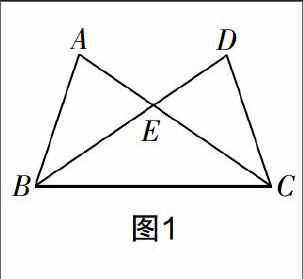
例如，在教学“等腰三角形的性质和判定”这一节时，笔者给学生设计了这样的一道题：如图1所示，有如下四个条件：①AB=DC；②∠ABE=∠DCE；③AE=DE；④∠A=∠D. 任取其中两个作为条件，不能得到△BEC是等腰三角形的是（ ）

A. ①与② B. ②与③

C. ①与④ D. ①与③

此题的前三个选项学生们都能准确地证明△BEC是等腰三角形，而第四个选项因为条件的原因，学生们无法证明△BEC是等腰三角形，因此学生觉得第四个选项不能证明△BEC是等腰三角形. 但是在学生们都不说话的时候，有位学生说第四个选项也能证明，就是分别过A，D两点作垂线，先根据“AAS”，再根据“HL”方能证明△BEC是等腰三角形. 听了这位学生的思路，笔者不禁为他的创新思维带来的精彩演讲所折服，看来这道题还需重新编写. 同时，也正因为这位学生的创新思路，让学生在不断质疑、反思的道路上越走越远，使得创新的思维越用越活.

可见，创新思维意识的培养也是十分重要的. 教师们要让学生大胆地构思，大胆地创新，不管对与错，学生们都会在创新中收获不同的感悟，长期训练，巧用“错题”，将帮助学生达到一个新的学习高度，营造高效的课堂.

总之，教师要时刻谨记新课程标准下学生的主体地位，打造以学生为主体的课堂. 师生间不断地交流，将学生的“錯误”资源转化成一笔巨大的财富，好好利用，培养学生的思维能力，养成良好的思维习惯. “错误”资源不仅会帮助学生反思自己，获得成长，也是打造高效课堂的有效方法.