留白
谢小丽
[摘 要] 课堂是教学的第一阵地,而作为教学主体的学生,他们的大部分知识也都来源于课堂. 因此课堂教育需要师生间的合作,教师应该把课堂交还给学生,学生也应该充分利用好课堂,不断尝试“走自己的路”——锻炼思维能力. 从多年的初中数学教学经历来看,笔者发现“留白策略”是促进学生思维发展的一把利刃,因此教师要扮演好引导者的角色,而不是“包办思想”,扼杀学生的思维能力. 巧用“留白策略”将极大程度地促进学生思维的发展.
[关键词] 初中数学;留白策略;思维能力
在初中数学这个环境下,学生们处在多方位发展的过渡期,有的学生甚至没有脱离小学的学习环境,没能迅速地融入初中的学习环境中. 而这个学习阶段也正是培养学生们思维能力迅速发展的黄金时期!因此,教师的教学目的就显得格外明确.
从实际的教学中,笔者发现“点化思想”可以说是最精湛的教学艺术,而“点化思想”的核心就是“留白策略”. 教師在教学的过程中,应该不时地给学生留白,让学生自己去思考,这样既可以使得学生思维能力的锻炼有所保障,也可以让学生们尝到成功的喜悦. 可以说“留白策略”是打开学生们思维之门的黄金钥匙!
问题情境下“留白”——激活思维动力
在初中数学学习的过程中,因为学生是教学的主体,但是初中阶段的学生们正处于青春期的过渡阶段,这个阶段的学生还比较童真,因此,教师在教学的过程中,就应该让教学方式符合这个阶段学生的学习习惯与学习乐趣.
大家都知道,问题是教学的指南针,而教师抛出问题就是为了让学生们深刻理解其中的道理并且吸取知识. 因此,笔者在教学的过程中,就充分利用“问题情境”,适当地留白,让学生们独自思考与总结,这将大大激发学生的学习兴趣以及好奇心,也有利于学生思维动力的养成.
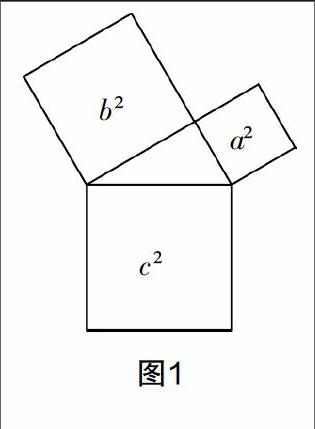
例如:在给学生们讲解“勾股定理”时,笔者为了激发学生的思维动力,首先提出一个情境问题:“人类发射太空探测器探测太空是否存在外星人,若存在的话,那么该如何与外星人交流呢?”然后给学生引入著名数学家华罗庚曾建议用反映勾股定理的树形关系图(如图1所示)与外星人进行交流. 接着再给学生抛出问题:“为什么要用勾股定理去交流?难道勾股定理的魅力那么大?”由此将学生们带入到勾股定理的学习中. 因为外星人对于初中生来说吸引力特别大,因此笔者牢牢抓住这一点,将教学情境赋予科学色彩,自然地激发了学生思维的动力,这样学生们就会在下面的学习过程中带着兴趣,收获事半功倍的效果!
倘若一上来就给学生们讲解什么是勾股定理,告诉学生们勾股定理的定义、公式,想必学生们会听得很无趣,吸收起来也会大打折扣. 而笔者通过举外星人的例子,通过开放式的问题作为课堂的教学情境,然后巧妙地布置留白,激发学生找寻到思维的动力点,让他们不由自主地进入到找寻未知答案的状态. 而学生们找寻未知答案的过程就是独立去填补教师留白的过程,这个过程将会对学生们吸取新的知识起到极大的帮助,十分有利于学生们的思维发展.
引导过程中“留白”——挖掘思维生长
当学生们适应了当下的教学环境之后,教师还应迅速地提出解决针对部分学生思维能力不强的方法:挖掘学生思维的生长点——引导过程中“留白”. 在新课改的教学标准下,教师要扮演好引导者的角色,要留给学生充分的思考时间和探究时间,只有这样才能激发学生的求知欲望,使其精神上得到满足. 学生们在进行积极的思维思考之前,心理上会出现一段“空暇”,教师就要利用好这段短暂的“空暇”,激活学生们的思维,从而挖掘学生的思维生长点.
例如:在给学生讲到“因式分解”这一节时,笔者给学生出示这样一个多项式:x2+1/2x+1/4,让学生们改变其中的一项,使得多项式成为完全平方式. 在让学生做题之前,笔者又给学生抛出了两个问题:一是怎样判断一个多项式是否为完全平方式;二是怎样配出完全平方式. 让学生先去思考第一个问题,他们经过仔细的思考给出了4种方法,接着再去问学生怎样才能配出完全平方式. 这时候学生就会通过对上面两个问题的总结,去研究原问题,得出:一是先确定首尾两项,再根据组成配出中间一项;二是先确定中间项和一个平方项,再根据组成分离出另一个平方项. 这时候就可以告诉学生们他们总结得很不错,这也正是我们所说的“知二求一”思想.
在出示x2+1/2x+1/4这个多项式的时候,笔者并没有告诉学生们如何去解,而是引导学生去思考,并且适当地“留白”,让学生们充分地进入到思考的状态中来,得出解答方案. 接着教师再对学生的思维“留白”过程进行总结,这样就能很好地完成一个探究过程. 在这样一个思维的引导过程中“留白”,使得学生从中找到了思维的生长点,凸显了“留白”的重要性.
探究操作下“留白”——促进思维共鸣
动态生成的有效形式之一就是操作探究. 教师在教学的过程中,要适当地在操作探究的过程中“留白”,这样不仅可以让学生们的思维产生停顿,而且帮助学生们在现有发展水平与最近发展水平之间架设了桥梁,可以达到一种虚中有实、虚中求实的效果. 教学在操作探究下“留白”将极大程度地触动学生的思维,使得师生间思维得以共鸣,大大地加强课堂的学习效率.
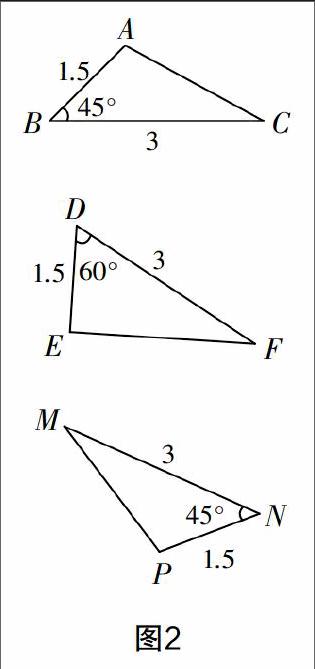
例如:在与学生们探讨到“两边一角情况下能否判定两个三角形全等”时,笔者引领学生用实验去证明. 每人拿出一张长方形纸剪出一个直角三角形,使得两条直角边分别为8 cm和6 cm,学生们互相比较,试问能得出什么结论. 其次,笔者利用教材上的图形(如图2所示),让学生们通过自己观察,然后猜想,再通过测量去验证自己的猜想,得出全等图形之间的特点. 期间,教师要让每一个学生都在认真地思考,不断地活跃自己的思维. 学生们通过测量△ABC和△PNM的其余条件,根据定义去验证全等,这时候笔者会问学生们剪下所画的△ABC能否与周围学生剪下的重合,由此能得出什么结论. 最后,用工具画出△ABC,让其满足①∠B=50°;②AC=4 cm;③AB=8 cm. 再次问学生剪下的△ABC能否与周围学生剪的完全重合,又能得出什么结论. 学生自主讨论,总结出规律.
通过用剪纸、测量以及画图等操作,引领学生们去探索三角形全等的条件,让学生们在收获了问题结论的同时,还领悟了探究的方法、相互合作的经验以及成功的喜悦,不经意间提高了学生们的交流能力. 因此,通过以上的探究例子,充分地让学生们的思维得以锻炼,学生们真正学到了知识,教师的教学也收获了相应的回报,在师生间达到了一种共鸣,也只有这样,学生的学习成绩才能得以真正提高.
课程小结中“留白”——升华思维衍生
所谓有始有终说的就是有开始就会有结尾,数学学习更是如此. 如果说问题是数学的第一阵地,那么解题的过程将是耕耘这片阵地最好的篇章. 而无论成与败,学生都要及时地总结. 在实际的教学过程中,教师要在课程的结尾处适当地“留白”,拿出足够的时间让学生在课上进行反思,再一次回顾课上所学,问学生们还有哪里不懂的,还想探究哪些知识等问题. 在有限的时间内让学生无限地遐想,必然大大提升学生的反思总结能力,让思维产生衍生点,使得学生产生进一步探求的欲望,从而牢记课堂的所学.
例如:讲解到“图形的旋转”这一课时,在课程小结中,笔者让学生回顾整节课所学的知识,提出自己不懂的地方,分享自己的经验等. 并且笔者还在学生的小结中“留白”,先是联系实际,让学生们去观察香港特别行政区区旗的紫荆花图案是如何形成的;再者拓展学生的知识,让学生阅读课外拓展材料,激发学生的兴趣,延伸思维空间;最后,由笔者自己总结,告诉学生要在变化中寻找到不变的真理,学会探索数学的内在规律,就会打开数学的大门,才能在数学的世界里如鱼得水.
通过在总结的过程中给学生的思维“留白”,让学生一整节课下来,还能抱有浓厚的兴趣,这样,就会大大地延伸学生们的思维,将课堂的教学向课外延伸,让学生的思维活动得以继续,让学生始终翱翔在知识的海洋中,将数学当作一种生活,好好地经营.
总之,教学之中“留白”是符合学生认知发展的一种科学的教学方式. 教师在教学的过程中,要时刻以学生为教学的主体,让学生在课堂中真正地学到知识. 适当地在教学中“留白”,放慢教学的步伐,让学生及时反思、总结与探索,将“留白策略”这把利刃发挥到极致,为迈向更高的数学境界而努力!

