E型热电偶动态特性实验研究与分析
高爱民 薛锐

摘要:以E型热电偶为研究对象,采用泓格I-7018温度采集模块、德国SiKA TP17650M检验仪设计了动态实验系统,通过Visial Basic和DCON Utility软件实现了实验数据的自动采集,完成了E型热电偶的动态特性实验,并使用MATLAB对实验数据进行了可视化研究,得出了该类型热电偶在不同偶丝直径、不同插入深度以及不同被测温度下的数学模型,为该类型热电偶在火电厂安装、检修时提供必要的理论基础与实践指导。
关键词:E型热电偶;动态特性,数学建模
中图分类号:TP212.11文献标识码:ADOI:10.3969/j.issn.10036199.2017.01.012
1引言部分
在火力发电厂中,虽然各类型温度传感器都有相应的安装规范与技术要求,但在施工过程中,由于施工人员的不能严格按照要求进行安装调试,经常会出现温度传感器损坏、测量回路异常、温度信号的阈值设置不合理等现象的发生,而这些故障或者事故的发生,往往会造成温度信号突变引起保护对象的误跳闸,进而引起保护误动作或拒动,造成机组的非计划减出力或停运,给电力系统带来巨大损失。
由于上述问题的严重性,国内外不少技术人员和专家都对该类问题进行过相关的研究与分析,做过诸如对温度传感器进行静态特性测试[1-2]的研究与分析、校验设计与测量数据处理[3-4]的讨论、同时也有对热电偶的动态特性[5-6]进行实验设计与研究、还有对该类问题进行过数学建模分析[7]。本文以E型热电偶为例,设计一套完整的动态实验系统,得出E型热电偶测温时,相对误差(精度)与插入深度、时间常数以及偶丝直径之间的关系,并且建立了对应的数学模型,为该类型热电偶在火电厂安装、检修、维护时提供必要的理论依据与实践指导。该实验系统包括校验仪(作为标准热源)、E型热电偶、热电偶信号采集模块、转换模块、电源和工控机,工控机通过RS232串口与转换模块I-7520、采集模块I7018、校验仪相连,由于热电偶的使用温度受材料规格和直径的影响,因此,K型热电偶的长度为15 cm,直径为2~5 mm,电源为DR7524开关电源,范围为10 V~30 V,电源供应器的额定功率大于整个系统的消耗功率的总和。
2.3实验步骤
1)开启电源,启动干式炉升温;运行应用程序,设定被测温度和采集时间,选择接收端口和采集周期; 当干式炉升温至设定温度并稳定时,将热电偶快速(形成类似于阶跃信号的输入)插入干式炉中,同时点击工控机界面上的“开始采集”按钮,实验开始;
2)在实验过程中,保持热电偶固定,直到響应曲线平稳,点击工控机界面上的“停止采集”按钮,将热电偶取出,点击工控机界面上的“保存数据”按钮,保存实验数据和图像;
3)当热电偶冷却至室温后,分别改变热电偶插入干式炉中的深度、干式炉的设定温度和热电偶的直径,重复步骤1)和步骤2),获得热电偶的插入深度、温度和直径的阶跃响应曲线,建立在不同热电偶直径条件下,相对误差与插入深度和温度之间的数学关系式、时间常数与插入深度和温度之间的数学关系式;从而很直观的看出热电偶插入深度、直径对热电偶测温性能的影响,对火力发电厂中不同的测温部位选择合理的热电偶温度传感器,以实现温度滞后的最小化有着一定的指导性作用。
2.4动态特性响应曲线
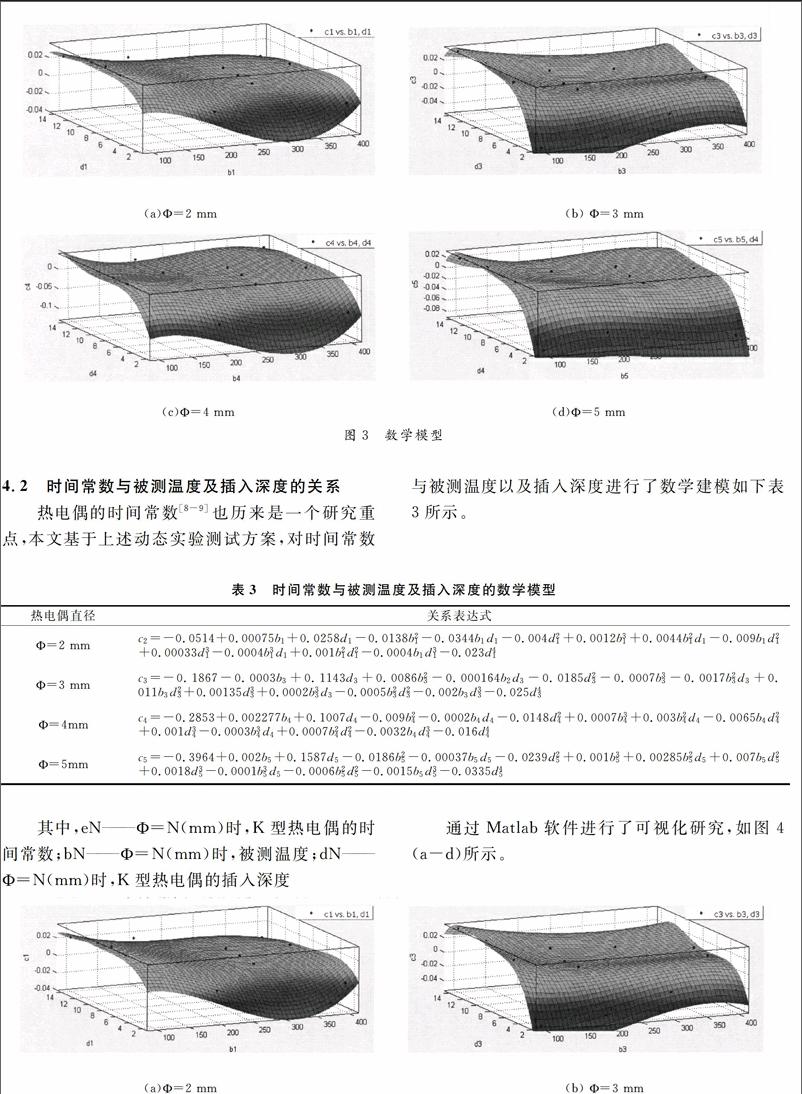
根据上述实验步骤,分别做了直径Ф=2 mm、Ф=3 mm、Ф=4mm、Ф=5 mm,温度点从室温分别到100 ℃、200 ℃、300 ℃、400 ℃时,插入深度与所测温度之间的阶跃响应曲线。
下面取一组实验数据,当温度为300 ℃时,热电偶的偶丝直径、插入深度与被测温度之间的阶跃响应曲线,如图2(a-d)所示。
从上述四组图像中可以看出:
1)阶跃响应曲线趋势一致;
2)热电偶的偶丝直径为过小时(Ф=2 mm),热电偶的阶跃曲线容易出现波动,误差比较大;
3)当Ф=4 mm、5 mm时,插入深度为2 cm已经不符合其安装规范,其响应曲线异于正常曲线,所测数据为错误数据;
4)时间常数随着温度阶跃变化量的增大,先呈现上升趋势,而后下降。
本次实验工作,完成了偶丝直径Ф=2 mm、Ф=3 mm、Ф=4 mm、Ф=5 mm,温度点从100 ℃、200 ℃、300 ℃、400 ℃的阶跃实验,所有这些实验数据趋势一致,与上面图例类似,由于篇幅所限,本文只选择其中一组进行分析与说明。
将上述数据带入上述相应数学表达式,计算E型待测热电偶的精度,符合其精度要求,说明上述数学模型可以方便快捷地验证所选热电偶精度、粗细、安装等是否合理,为电力生产过程中的E型热电偶的选型、安装提供了一定的理论与实验依据。
5结论
综上,本文以E型热电偶为研究对象,对直径为Ф=2 mm、Ф=3 mm、Ф=4 mm、Ф=5 mm的热电偶通过阶跃响应实验完成了数学模型的可视化研究,并验证了该数学模型的准确性,得出以下四点结论:
1)插入深度对测量误差的影响尤为明显,对于本文所用E型热电偶,其插入深度要求为直径的15~20倍,而文中热电偶插入深度为2 cm时,不符合安装规范,其相对误差也较大。
2)插入深度与相对误差并不成线性关系,而是相对误差随着插入深度先减小,后增大。
3)在允许测量范围内,热电偶测量的相对误差随着被测温度的升高而降低。
4)热电偶直径越小,显示温度越容易出现波动,越容易产生误差,对于系统稳定是不利的。
5)热电偶直径越小,时间常数越小;该热电偶的时间常数随温度阶跃变化量的增大,先呈上升趋势,而后又有所下降,随后呈现较大幅回升,预测变化趋势为随温度阶跃变化量逐渐升高。
参考文献
[1]赵兵,杨基峰.基于LabVIEW的传感器静态特性标定系统[J].仪表技术与传感器,2011,(6):20-22.
[2]杨宇,郝晓剑,周汉昌.热电偶动态校准及动态补偿技术研究[J].光电技术应用,2013,28(6):77-80.
[3]崔巍.温度测量系统现场检定方法的研究[J].同煤科技,2013(4):32-34.
[4]WINKLER R,WOOLLIAMS E R,HARTREE W S,et al.Calibration of an Absolute Radiation Thermometer for Accurate Determination of FixedPoint Temperatures[J].Int J Thermophys,2007,28:2087-2097.
[5]刘宗瑞,成婉婷,刘志远.热电偶动态响应测试系统[J].传感器与微系统.2014,33,6:82-85
[6]ANTHONY B,DICKINSON S,BEYOND B.“fire temperatures”:calibrating thermocouple probes and modeling their response to surface fires in hardwood fuels[J].Canadian Journal of Forest Research,2008,38(5):1008-1020
[7]徐宏宇,朱永麗.基于PID神经网络的热电偶数学模型研究[J].电子设计工程.2011,19(22):45-47
[8]滕士雷,孔喜梅.基于阶跃温度响应的热电偶时间常数测试系统[J].中国测试,2011,37(1):24-27.
[9]闰洁.调制激光器激励法的热电偶时间常数测试[J].仪表技术,2010(11): 8-11.第36卷第1期2017年3月计算技术与自动化Computing Technology and AutomationVol36,No1Mar. 2 0 1 7第36卷第1期2017年3月计算技术与自动化Computing Technology and AutomationVol36,No1Mar. 2 0 1 7

