抵御执行器故障的H静态输出反馈可靠控制

徐艺超 姚波 王福忠

摘要：针对线性系统，考虑连续增益故障模型，研究了具有执行器故障的H

关键词：执行器故障；静态输出反馈；线性系统；可靠控制；线性矩阵不等式（LMI）

中图分类号：O231.1文献标识码：ADOI：10.3969/j.issn.10036199.2017.01.003

1引言

反馈控制是指在控制系统中，将系统的实际输出和期望输出进行比较，形成误差，从而为确定下一步的控制行为提供依据，实现对被控对象进行控制的任务，这就是反馈控制原理。文献[1]提出了不确定时滞系统的反馈控制问题，并且给出了当执行器发生故障时，系统鲁棒镇定的条件。文献[2]基于线性矩阵不等式给出了保成本可靠控制器的的参数化表示。文献[3]利用凸组合方法，得出当执行器发生故障时，系统渐近稳定的条件。目前反馈控制中主要是动态输出反馈和状态输出反馈，动态输出反馈结构复杂消耗能量，状态输出反馈需要系统对状态进行采集，但一般很难做到。目前，静态输出反馈相对于动态输出反馈和状态输出反馈研究的学者较少。文献[4]给出了线性系统静态输出反馈镇定的LMI方法。文献[5]利用线性矩阵不等式方法设计了随机混合系统的无脉冲以及随机稳定的静态输出反馈控制器。文献[6]通过构造一个二次Lyapunov函数，结合线性矩阵不等式的约束条件，给出了控制器存在的充分条件。以上文章涉及到的静态输出控制都不是可靠的，一旦系统的传感器或者执行器发生故障，系统将不再稳定，所以设计一个静态输出可靠控制是必要的也是具有实际意义的。可靠控制是将系统可能发生的故障考慮在系统控制器的设计过程中，其设计主要考虑系统的是执行器和传感器故障，故障类型分为“中断”故障和增益故障，“中断”故障也称为离散故障，增益故障也称为连续故障，本文主要研究连续故障。自1980年Siljak发表关于可靠镇定的文章以后，许多学者对其进行了深入研究[7-9]。文献[10]给出了在连续故障的前提下，基于LMI方法给出了反馈控制器存在的充分条件，并且提出了考虑执行器和传感器双故障的系统的完整性设计方法。文献[11]以执行器故障诊断为前提，解决了连续时间系统的可靠时滞控制问题。自从上个世纪年90代初由Zames[12]提出

2问题描述

考虑线性定常系统：

4数值仿真

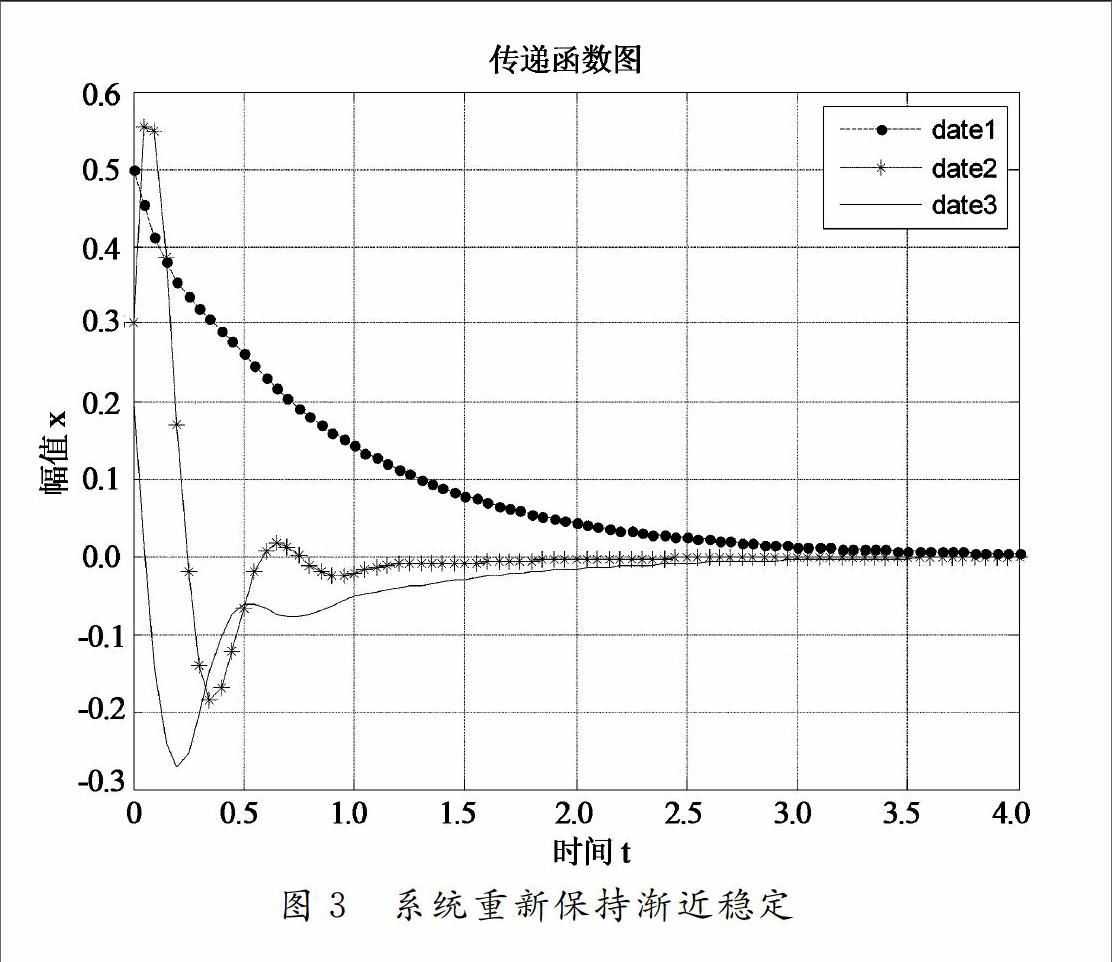
本文研究的是，首先考虑正常的线性系统在无故障的情况下，通过设计带有H

SymboleB@ 性能指标的静态输出反馈控制器使闭环系统保持稳定；再考虑正常的线性系统发生执行器故障，系统出现不稳定的情况，通过重新设计控制器，使系统达到稳定。

考虑如下系统：

5结论

考虑线性系统，本文研究了具有执行器故障的H

SymboleB@ 性能指标的静态输出反馈可靠控制问题。首先我们讨论了在不考虑故障的情况下，通过设计控制器使系统保持稳定；然后系统发生故障，在原控制器的作用下，系统无法保持渐近稳定；最后针对同一系统同一故障，通过重新设计可靠控制器，使系统重新保持稳定。文章中的数值仿真以及极点配置图像证明了可靠控制器的有效性。

参考文献

[1]徐兆棣，张嗣瀛.不确定时滞系统的输出反馈可靠控制[J].东北大学学报，2000，21（6）：583-585.

[2]任俊超，胡刚，谢湘生.不确定广义系统的保成本可靠控制[J].系统工程与电子技术，2003，25（9）：1122-1134.

[3]刘玉忠，王立敏，史书慧.确定切换系统的可靠控制[J].计算技术与自动化，2007，26（3）：17-20.

[4]WANG Jinzhi，ZHANG Jifeng.AN LMI.ApproachI to Static Output Feedback Stabilization of Linear System[J].Control Theory andApplication，2001，18（6）：843-846.

[5]BOUKAS E K. Static output feedback control for stochastic hybrid systems： LMIapproach[J].Automatica，2006，42（1）：183-188.

[6]WANG Junwei，WU Huaining，LI Hanxiong.Static output feedback control design for linear MIMO systems with actuator dynamics governed by diffusion PDEs[J]. International Journal of Control，2014，87（1）：90-100.

[7]VEILLETTE R J，MEDANIC J V，PERKINS W R. Design of reliable control system[J].IEEE Transaction on Automatic Control ，1992，37（3）：770-784.

[8]王福忠，姚波，张嗣瀛.具有执行器故障的保成本可靠控制[J].东北大学学报，2003，24（7）：616-619.

[9]MA Lichao，MENG Xiuyun，LIU Zaozhen，et al.Multiobjective and reliable control for trajectorytracking of rendezvous via parameterdependent Lyapunov functions[J].Acta Astronatica，2012，81（1）：122-136.

[10]王福忠，姚波，张庆灵.基于LMI双故障动态输出反馈完整性控制[J].控制理论与应用，2006，23（6），976-980.

[11]乔军丽，贾新春，刘博.具有执行器故障的连续时间系统的可靠时滞控制[J].中北大学报报，2006，27（2）109-111.

[12]ZAMES G.Feedback and Optimal Sensitivity：Model Reference，Transformations，Multiplicative Seminorms，and Aroximate Invers[J].IEEE.e Transactions on AutomaticControl ，1981：AC-26（2）： 301-320.

[13]伏玉笋，田作华，施颂椒.不确定非线性系统的H

SymboleB@ 状态反馈可靠控制[J].应用科学学报，2000，18（3），280-282.

[14]滕青芳，范多旺，严伟.不确定时变时滞系统的保成本H

SymboleB@ 鲁棒可靠控制[J].兰州交通大学学报，2010，29（6），74-78.

[15]GE D，WANG Fuzhong，YAO Bo.Static Output Feedback Reliable Controlwith Actuator Failures[M].Industrial Engineering，Machine Designand Automation & Computer Science and Application.Sanya：World Scientific，2014：479-483.

第36卷第1期2017年3月计算技术与自动化Computing Technology and AutomationVol36，No1Mar. 2 0 1 7第36卷第1期2017年3月计算技术与自动化Computing Technology and AutomationVol36，No1Mar. 2 0 1 7