初中数学开放式课堂的创建途径探索
孙彪

[摘 要] 有效教学需要一个开放的环境,优质思维更需要一种开放的意识. 随着教学要求的更新与提高,初中数学愈发需要通过开放课堂教学的各个环节来实现整体教学效果的强化. 因此,教师们需要快速探索出一条开放式课堂的创建路径,进行根本性、全方位的着手,推动课堂教学事半功倍.
[关键词] 开放式课堂;途径;探索
数学知识的高效学习离不开广泛的数学思维. 只有让学生从思维的角度灵活起来,才能更加妥善地应对多变的知识内容,实现学习效果的不断提升. 为了达到这种灵活思维的目标,就需要从课堂教学环节入手,将教学视野不断拓展,从问题内容、活动形式、指导思想等入手,打造出一个真正开放的数学课堂,让学生从根本思维上收获一个进步性的跨越. 为了实现这种教学效果,笔者在实践中尝试了多种开放式课堂的创建途径,并将其中行之有效的几种总结成文.
开放教学主角,搭建互动平台
初中数学的教学主角只有教师吗?当然不是. 除了教师之外,还有学生. 从很大程度上来讲,学生作为教学主角的重要性要多于教师. 既然学生才是数学知识的最终接受者,所以,只有学生真正理解、掌握了数学知识方法,才能说是将教学活动落实到位了. 因此,在课堂教学的主角方面开放出一个缺口,更多地将学生这个教学主体重视起来,是创建开放式课堂的根本.
例如,为了深化学生对反比例函数内容的理解,笔者先向大家提出了这样一个问题:如图1 ,反比例函数y=(x>0)和矩形ABCD均位于平面直角坐标系的第一象限,其中,AD与x轴平行且长为4,AB的长为2,点A的坐标是(2,6). 那么,点B,C,D的坐标分别是什么?这个问题的难度并不算大,学生结合所学知识很快就会得出答案. 接下来,笔者又将问题进行延伸:如果将这个矩形向下进行平移,使得它的两个顶点同时与反比例函数的图像相交,那么,应当将这个矩形平移多少?该反比例函数的解析式又是什么?在笔者的逐步设问中,学生与笔者形成了很好的互动,并在笔者的问题带领之下,很自然地走向了思维的深入.
强调学生为教学主体的最好方式就是带领学生真正走进数学课堂当中,让学生亲身参与到知识的产生与发展过程中. 当然,这种自主处理知识的能力,并不是初中阶段的学生所能熟练具备的,这便需要教师从旁进行辅助、引导. 与学生互动,能让学生在潜移默化中融入课堂,这无疑是一个十分高效的途径.
开放教学媒介,运用现代技术
随着时代的飞速发展,各种现代化的技术手段不断出现,其中很多更是可以运用于数学教学当中,这也就为教学方式的开放式设计提供了前提基础. 在以往的课堂教学当中,教师大多采用的是语言叙述与板书书写相结合的传统方式,这种方式早已让学生感到习以为常,很难再对数学课堂产生兴趣,教学实效也并不是多么理想. 但当现代技术手段运用到课堂教学当中之后,效果便会完全不同.
可以帮助数学进行教学的现代技术手段有很多,教师可以根据当前教学内容的特点与需求分别进行选择. 这种新元素的加入,为初中数学课堂带来了全新的气息. 无论教学内容如何,这种教学手段首先就已经将学生的关注热情激发起来了. 接下来,借助现代技术手段的全方位呈现阐释,学生便会看到数学内容的每个角落、层面,能逐步实现对知识方法的全面认知.
开放教学输出,强化实践能力
开放式课堂教学的建立还表现在知识内容的输出路径上. 在绝大多数情况下,学生接触数学知识都是从理论的角度入手的,但这并不是数学知识的全部面貌. 如果學生的视野始终局限在理论的范围之内,未免会让初中数学变得狭隘. 只有将抽象的理论与灵活的实践应用联系起来,才能实现立体全面的教学效果. 因此,从增强实践的角度开放教学输出路径,也是我们将要讨论的一个重点.
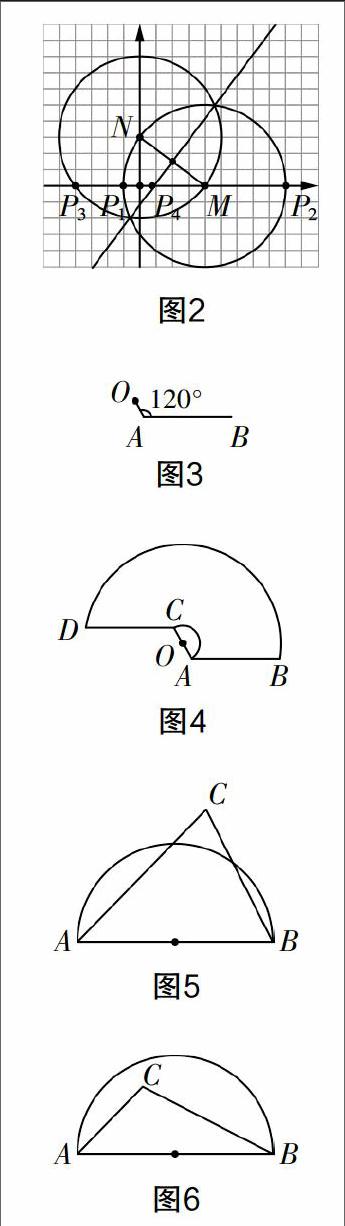
例如,在对三角函数的内容进行教学时,笔者在课堂上引入了这样一道实践题:汽车后玻璃上的雨刷器可以看作一条折线OAB(如图3),其中,量杆OA的长是10厘米,雨刮杆AB的长是48厘米,∠OAB为120°. 雨刷器打开后,AB可以扫到CD的水平位置(如图4). 那么,AB运动的最大角度及O,B之间的距离分别是多少?AB所扫过的最大面积又是多少(结果可带根号)?这样的实践问题,彰显了更加真实、细致的数学理论,可谓达到了学习的双赢.
对于初中数学来讲,实践是一种必备的能力. 它是将理论知识引入生活实际的一条纽带,更是促使理论知识理解走向具体深入的一条捷径. 如果能够将知识教学的出口开放拓展,让每一次理论教学都能够以实践的方式加以印证,将会收获事半功倍的教学实效. 实践能力的强化,同时也是对学生数学知识能力的横向拓展.
开放教学方法,大胆灵活探究
广泛的教学内容所对应的自然是种类繁多的教学方法. 只有从方法上加以丰富,才能更好地契合不同知识内容的特点需求,优化教学效果. 很多学生总认为自己的学习能力还不够强,难以处理较为灵活、复杂的探究性问题,造成自己在考试当中遇到类似问题时也总是无所适从. 这种想法是不正确的. 探究性思维是各个数学学习阶段都需要经历和具备的,更应在初中教学阶段予以突出和强调.
例如,在对三角形的基本性质进行教学时,为了让学生对其进行更为深入的理解,笔者请学生试着探究如下问题:在一个半圆中,AB是它的直径. 如图5,点C位于半圆之外,如图6,点C位于半圆之内. 如果你的手中只有一把没有刻度的直尺,能否找出图5中△ABC三条高的交点?能否找出图6中△ABC中AB边上的高?相比于基础知识的文字性描述来讲,这种方式显然灵活许多. 起初,学生感到这种问题有一定的难度,但亲手操作过后,会逐渐找到该问题与三角形基本性质之间的关系,在完成探究的同时深化了对相应知识的理解.
与基础性知识的学习相比,探究性问题的研究显然具有更大的难度. 对此,不能将开展探究的任务全部抛给学生. 通过不断开放的教学方法,将探究的元素逐渐渗透到课堂当中,学生便可以在自己的数学思维当中自然加入探究的意识. 当这种意识成为一种思维习惯之后,学生在接受数学探究时就会自然许多,学习效果也会随之得到提升.
开放思想指引下的初中数学课堂,较之从前明显灵活、生动了许多. 从知识内容本身来讲,开放式的教学将数学知识拓展出了很多维度,让学生的知识视野得以打开. 从数学思维能力来讲,开放式的教学为学生的能力提升预留出了更多空间,能让大家在自由的空间探寻到数学的真谛. 作为整个数学教学过程的基础阶段,如果学生能够在这个时候就习惯这种开放式的课堂设计,并且从中获得预期的能力层面的提升,便是对接下来长远学习的最大助力,这也是创新、强化初中数学课堂教学设计的理想途径.

