以函数图像为载体的平面几何问题探究

☉浙江省柯桥中学 徐忠华

以函数图像为载体的平面几何问题探究

☉浙江省柯桥中学 徐忠华

如何提高学生的解题能力，是数学教学研究的重要课题之一.通过平时的练习测验发现，不少学生解题时思路开阔，条理清晰，方法灵活；但也有相当一部分同学分析问题和解决问题的能力较差.造成这种差别固然有多方面的因素，但作为数学教师却不能不多从教学上去探究原因.爱因斯坦曾经说过：“提出一个问题往往比解决一个问题更重要.”数学的各种理论无一不是数学问题解决的结果.正如美国数学家哈尔莫斯所说：“数学存在的主要理由是解题.因此，数学真正的组成部分是问题和解，其中问题是数学的心脏.教师要善于发现并归纳问题的类型，并且引导大家有针对性地对于这些问题展开分析与探究.这样才能够帮助学生更好地意识到问题的症结，并且找到好的处理方式.经过有效的训练过程的不断积累后，学生的解题能力自然会得到明显的进步与提升.

在知识交汇处命题是高考或模拟试题中的重要形式，其中代数与几何的交汇又是常见题型，此类问题体现了数与形的有效结合，能够考查学生对知识的掌握程度以及综合运用所学知识灵活解答的能力.本文对一类以基本初等函数图像为背景的平面几何问题进行探究.

例1如图1所示，A是函数f（x）= 2x的图像上的动点，过点A作直线平行于x轴，交函数g（x）=2x+2的图像于点B，若函数f（x）=2x的图像上存在点C使得△ABC为等边三角形，则称A为函数f（x）=2x上的好位置点.函数f（x）=2x上的好位置点的个数为（）.

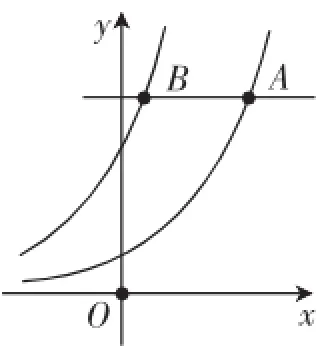
图1

A.0B..1C..2D.大于2

本题以指数函数为背景，结合平面几何中等边三角形，以新定义的形式展现出来.形式新颖、内涵丰富，能有效考查学生对所知识的综合能力以及分析问题、解决问题的能力.

一、条件审视

解题是从条件审视开始，充分、准确地利用条件是问题顺利求解的关键.对于本题已知条件的处理，要审清如下几个问题：

（1）题目条件中给了两个函数，即f（x）=2x，g（x）=2x+2，这两个函数之间有什么关系？

函数g（x）=2x+2可由函数f（x）=2x向左平移两个单位得到，据此可判断点A与B的横坐标之差为2，即|AB|=2.

（2）AB平行于x轴，可得出哪些有用信息？

由AB平行于x轴可知，A、B两点的纵标相等.

（3）若存在△ABC为等边三角形，那么等边三角形具有什么性质？根据这些性质可得出哪些结论？

联想等边三角形的相关性质，可知点C的横坐标与AB中点的横坐标相等；由xB＜xC＜xA知，yC＜yA；点C到AB的距离为，所以点C的纵坐标可由点A或B的纵坐标减求得.

二、问题解答

条件审清之后问题的解答就水到渠成了.

若函数f（x）=2x的图像上存在点C，使得△ABC为等边三角形，如图2所示.设直线AB：y=c，因为A是函数f（x）=2x的图像上的动点，所以A（log2c，c）.

同理B（log2c-2，c）.

所以|AB|=log2c-log2c+2=2.

图2

因为点C在函数f（x）=2x的图像上，所以c的值唯一，故函数f（x）=2x上的好位置点的个数为1.评析：本题主要考查了指数、对数的运算，指数函数与对数函数的图像和性质，以及平面几何性质的应用.

三、变式演练

1.变换问题的背景

例2如图3，点A，B在函数y=log2x+2的图像上，点C在函数y=log2x的图像上，若△ABC为等边三角形，且直线BC∥y轴，设点A的坐标为（m，n），则m=（）.

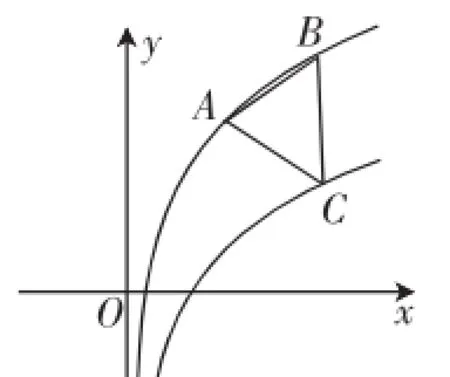
图3

图4

本题从形式上看，将背景函数由指数函数变换为对数函数，问题的求解方法与例1如出一辙.

解析：如图4所示，过点A作BC的垂线，交BC于点D.

由A（m，n），可得xC=xD=m+，yC=n-1，yB=n+1.

将点A的坐标代入函数y=log2x+2，得

n=log2m+2.①

将点C的坐标代入y=log2x，得

n-1=log（2m+）.②

将式②代入式①，得log2m+2-1=log（2m+），整理得log2（m+）-log2m=1，即log2=1，所以=2，解得m=

评析：本题与例1如出一辙，只是将背景函数改为对数函数，解题的关键是把握平面几何的几何性质以及准确进行指数、对数的运算.

2.变换问题的目标

例3如图5所示，点O为坐标原点，点A（1，1）.若函数y=ax（a＞0，且a≠1）及y=logbx（b＞0，且b≠1）的图像与线段OA分别交于点M，N，且M，N恰好是线段OA的两个三等分点，则a，b满足（）.

A.a＜b＜1B.b＜a＜1

C.b＞a＞1D.a＞b＞1

图5

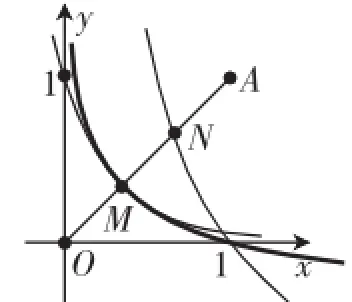
图6

解法1：由图像易知，0＜a＜1，0＜b＜1.

因为M，N是线段OA的两个三等分点且A（1，1），所

又因为点MN分别在函数y=ax及y=logbx的图像上，

所以a＜b＜1.

解法2：由图象易知0＜a＜1，0＜b＜1.

因为点O为坐标原点，A（1，1），所以直线OA为y=x.

因为y=ax过点M，所以其反函数y=logax亦经过点M，且过点（1，0），其图像如图6所示，在函数y=logax及y=logbx中令y=1，得x=a，x=b，结合图像易判断a＜b＜1.

评析：本题考查了对数函数与指函数的图像和性质，以及对数函数与指数函数互为反函数关于直接y=x的对称性.

3.变换问题的形式

例4已知点A在曲线P：y=x2（x＞0）上，⊙A过原点O，且与y轴的另一个交点为M.若线段OM，⊙A和曲线P上分别存在点B、点C和点D，使得四边形ABCD（点A，B，C，D顺时针排列）是正方形，则称点A为曲线P的“完美点”.那么下列结论中正确的是（）.

A.曲线P上不存在“完美点”

B.曲线P上只存在一个“完美点”，其横坐标大于1

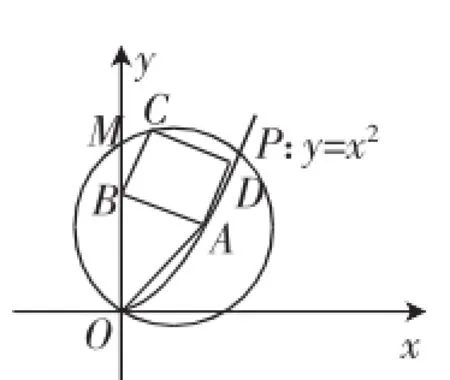
图7

图8

接下来考虑当点A的横坐标越来越大时∠BAD的变化情况.

设A（m，m2），当m＜1时∠AOy=，此时圆T与y轴相离或相切时，点A不是“完美点”，所以只需考虑m≥1，且当m增大时，∠BAD越来越小且趋近于0.而当m=1时，∠BAD＞，故曲线P上存在唯一一个“完美点”其横坐标大于1.

过点A作AH⊥y轴于点H.分别过点A，D作x，y轴的平行线交于点N.先考虑∠BAH，cos∠BAH=，于是m增大时，cos∠BAH减小且趋近于0，从而∠BAH增大，且趋近于

再考虑∠DAN，D（n，n2），则tan随着m的增大，OA的长增大，AD=OA也增大，于是m+n增大，从而tan∠DAN增大，∠DAN增大且趋近于所以∠BAD=π-∠BAH-∠DAN随着m的增大而减小，且趋近于0.

评析：本题以新定义为视角，综合考查了二次函数及平面几何中圆的性质.通过假设点A为“完美点”，设A（m，m2）结合图像，通过讨论m＜1及m≥1的情况，得出答案.

综上，解答以函数图像为背景的平面几何综合问题，充分把握平面几何图形的性质、相关的运算以及准确分析判断图形之间的位置是问题顺利求解的关键.