一道课本习题的探究及思考

☉浙江省杭州市余杭实验中学 王国军

一道课本习题的探究及思考

☉浙江省杭州市余杭实验中学 王国军

一、背景

著名数学教育家波利亚说：“一个专心认真备课的教师能够拿出一个有意义的但不复杂的题目去帮助学生挖掘问题的各个方面，使得通过这道题，就好像通过一道门户，把学生引入一个完整的理论领域.”学生的思维是灵动的和多向的，教师要不断地激发他们的兴趣，拓展他们的思维空间，使他们的潜能得到最大限度的发展.而对课本习题进行变式探究是一条十分有效的途径.通过改变条件，让学生对满足不同条件的情况作出正确的分析；通过改变结论等培养学生推理、探索的能力；通过推广引申，使学生在深入探究中认清问题的本质.这些变式探究可以培养学生的发散思维能力，使学生的认知能力得到较大地提高，有效地提升学生的数学思维能力.下面笔者以一道解析几何题为例，谈一谈变式探究的方法和自己的教学思考.

二、题目

已知△ABC的两个顶点A，B的坐标分别是（-5，0），（5，0），且AC，BC所在直线的斜率之积等于m（m≠0），试探求顶点C的轨迹.（新人教A版高中课本选修2-1第80页复习参考题A组第10题）

三、探究过程

在讲这道题目之前，我让学生预习了这道题目，许多学生运用直接法顺利地完成了解答.

解：设顶点C的坐标为（x，y），

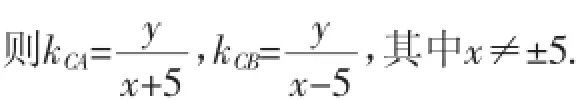
化简，得mx2-y2=25m（x≠±5，m≠0）.

分类讨论如下：

（1）当m=-1时，得x2+y2=25（x≠±5），此时C的轨迹是圆心在原点，半径为5的圆（不含A和B两点）；

讲完这道题后，我试着问学生：分类（1）反过来成立吗？

探究1：圆x2+y2=25上任意一点（除A，B之外）与A，B的连线的斜率之积为定值吗？

学生开始积极思考和演算，很快得出结论：

当在圆x2+y2=25上任取异于A（5，0）和B（-5，0）的一点M，因为AB是直径，直径所对圆周角为直角，AM和BM互相垂直.所以AM与BM的斜率乘积为定值-1.

在学生尝到一点收获的甜头后，我抛出了一个问题：圆和椭圆有非常密切的关系，椭圆是否和圆具有类似的性质？学生在讨论后形成了以下问题：

学生们经过一番思索和演算后，形成下面的解答过程：

解：设M（x0，y0）是=1上任意一点，则1.①

假设kMA×kMB=m，即=m，所以

此时，我引导学生观察这个定值的特征：a2=25，b2= 16，即m=-于是抛出了又一个问题：是否可以猜想：在任意椭圆的情况下也有类似结论？随后我将问题展示在屏幕上：

在几番讨论和争执后，学生们得出了结果，我请一位学生把过程板书了出来：

解：设椭圆上任意一点M的坐标为（x0，y0），则=1.①

由题意知，A（1-a，0），A（2a，0），

没有想到，这名学生还没有写完，下面就有个同学站起来说：我发现焦点在y轴上的椭圆上任意一点与长轴端点连线的斜率乘积也是定值！我把他提出的问题展示在屏幕上：

然后请他上来板书过程如下：

解：设椭圆上任意一点M的坐标为（x0，y0），则=1.①由题意知，A1（0，a），A2（0，-a），

结果，学生们通过自己的探索得到这样的结论：

（1）焦点在x轴上的椭圆上任意一点与长轴端点连线的斜率乘积为定值

（2）焦点在y轴上的椭圆上任意一点与长轴端点连线的斜率乘积为定值

虽然下课铃声响了，但学生们还沉浸在发现新知识的喜悦当中，讨论不休，几个学生冲到我面前，提出了两个新的问题：

我特别肯定了他们的积极参与思考，鼓励他们动手先自己算一下，然后再师生一起讨论.结果第二天刚进教室，许多学生就把他们的探究结果给我看：

解：设双曲线上任意一点M的坐标为（x0，y0），则

由题意知，A1（-a，0），A2（a，0），

于是，他们得到的结论是：焦点在x轴上的双曲线上任意一点与长轴端点连线的斜率乘积为定值.同时他们也推证了：焦点在y轴上的双曲线上任意一点与长轴端点连线的斜率乘积为定值.因为在前面我和学生一起用“点差法”推证过椭圆和双曲线中点弦公式，学生们还提出了椭圆和双曲线的这四个结论和它们的中点弦公式完全对应的看法.

这些结果是让我始料不及的，尽管这些要推出来并不是很难，但学生并没有因为我没有要求就停止探索，这种精神出现在我的学生身上，我非常激动！如果说前边的探究1到3是我提出问题，学生分析回答问题，那么后面的则完全是学生积极主动探索的结果.虽然我任教的两个班学生的数学素养并不高，但现在他们积极参与的态度和获得的结果来看，说明他们对数学的兴趣很高，而且可以模仿提出一些类似的新问题，有了一定探索意识.

四、几点思考和感悟

通过该例题的深度剖析和变式探究，不仅巩固、加深已学过的知识，而且汲取主干中的营养，生发出新的枝叶，进而能培育出知识和能力的参天大树.基于以上案例分析，笔者认为在变式教学中应遵循如下原则.

1.内容要有针对性

变式要有的放矢，应根据教学目标变式，应根据知识点在整个知识结构中的纽带作用进行变式，要充分了解学生的知识、方法、经验、兴趣和思维特点等，遵循学生的认知规律，在知识的易错、易混淆处变式，在知识交汇处变式，在思想方法交融处变式，在知识拓展延伸处变式.本题变式探究的内容（定值问题）既是解析几何中的核心知识点，并蕴含着重要的数学思想方法，同时也是解析几何中能推广引申、揭示数学本质的典型素材.

2.内容难度应该可行

教师应在学生的“最近发展区”内进行变式，过分简单的变式题组会影响学生的思维质量，思维活动未得到充分展开，缺乏应有的激励作用，难度太大的变式题组容易挫伤学生的积极性，学生难以获得成功的喜悦.变式题组的设计要注意小坡度、密台阶，层层递进，螺旋上升，有利于学生逐步深入，变式既要注重面上拓展，又要注意纵向深入，发挥例题的辐射作用，促进技能思维定式的正迁移，有效地将知识深化，把握形同质异题的处理策略，从而达到通一类、带一串、建构知识网络揭示解题规律，使探究教学有效、高效.例如围绕本题的第一问证明，笔者编制三道符合学生认知水平、层层递进的变式，这三道变式题都是定值问题，笔者引导学生展开递进式探究，从而归纳提炼出解决这类问题的基本方法和策略：引进适当的参数，运用设而不求、整体代换的策略.

3.习题的结论可以推广

猜想是对研究的对象和问题进行观察、实验、比较、归纳等，依据已有的知识作出符合一定经验与事实的推测性想象的方式.在教学中，教师要创设学习契机引导学生进行发散性思考，培养学生勇于猜想、推理，通过观察、分析、比较、联想等方式，实现对已有事实和结论的推广.本题在进行了一题多变后没有结束探究，而是此基础上引导学生猜想、引申、推广，从而发现本题的一般性规律，揭示了问题的本质，找到了该题的“题根”及源头.学生的创新思维得到了升华，这对于培养学生提出问题、发现问题的能力具有重要的作用.

波利亚曾形象地指出：“好的问题同某种蘑菇有些相像，它们都成堆地生长，找到一个以后，你应当在周围找一找，很可能附近就有好几个.”创新的程度直接依赖于努力钻研的坚韧程度.高三数学解题教学中由一个基本问题出发，运用特殊化、一般化、分解、重组、增加背景、改编要素以及类比、联想等思维方法，探索问题的发展变化，使我们发现问题的本质，主动地克服思维的心理定势，变中求进，进中求通，常给人以新鲜感，能够唤起学生的好奇心和求知欲，激发其参与教学活动的兴趣和热情，让学生感悟到数学课堂的独特魅力，从而拓展了学生的思维空间.