例谈三角函数试题的求解策略

☉浙江省宁海县知恩中学 王丽亚

例谈三角函数试题的求解策略

☉浙江省宁海县知恩中学 王丽亚

近几年来，各省高考对三角函数部分的考查，在内容、题量、分值三个方面保持稳定的同时，加重了对三角函数性质的考查，难度适中.这样的命题意在考查学生的计算能力、演绎推理能力、综合应用知识解决问题的能力以及数学思想方法的应用，激发了学生进一步学习的潜能.对应思想作为数学中的一个重要思想，近几年来不断在高考三角函数图像与性质的相关问题中出现，成为高考题型中的一个创新.笔者根据近几年的教学实践，总结了一些解决三角函数题时的基本方法，仅供参考.

一、利用导数巧解三角函数题

导数是研究函数性质的一个很重要的工具，利用导数可以很容易解决函数的极值、最值和函数的单调性等问题.三角函数作为一种特殊的函数，导数这个工具自然也适合三角函数.

1.利用导数求三角函数值

我们知道，形如y=Asin（ωx+φ）+k（y=Acos（ωx+φ）+ k）的三角函数f（x）对称性有其特殊性：对称轴x=x0处必为极（最）值点，从而f′（x0）=0.

常规解法此略，运用导数解此题：

2.利用导数证明三角恒等式

例2证明：sin2αsin2β+cos2αcos2β-

分析：本题若采用常规的三角函数的化简方法，都比较复杂.考虑到要证明的结果是一个常数，我们只需把左边看成α或β的函数，证明该函数的导数恒等于零，然后取一个特殊角求出这个常数即可！

证明：构造函数f（α）=sin2αsin2β+cos2αcos2βcos2β.

求导数得f′（α）=2sinαcosαsin2β-2cosαsinαcos2β+ sin2αcos2β=sin2α（sin2β-cos2β）+sin2αcos2β=-sin2αcos2β+ sin2αcos2β≡0，

故f（α）为一常数，

而f（0）=cos2β-

所以sin2αsin2β+cos2αcos2β-

3.利用导数求三角函数的最值

令f′（x）=0⇒bsinn+2x-acosn+2x=0⇒tann+2

为方便起见，即满足上述方程的解为x0，由sinx和 cosx在上的单调性可知，x0为函数（fx）唯一的极小值点，从而为最小值点.利用解得

从而

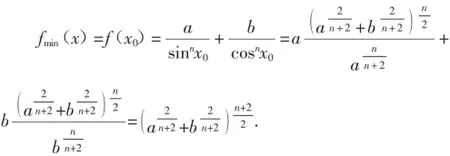
二、利用对应思想巧解三角函数问题

我们所说的对应是人的思维对两个集合之间联系的把握，反映的是两个集合元素之间的关系.对应将各种类别、各种层次的对象联系起来，呈现出它们之间各种各样的属性，使得各种数学对象能够互相结合、互相转化和深入.运用对应思想方法，通过三角函数图像之间的对应关系，求解近几年来高考中的三角函数图像与性质的相关问题，大大简化计算，起到了事半功倍的效果.

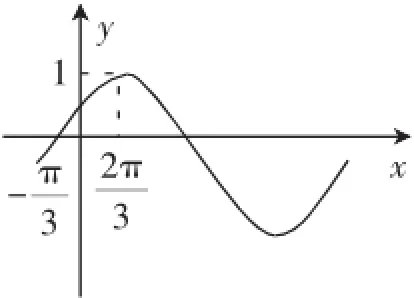
图1

无论是传统法还是对应法，都很好地利用了图像上的特殊点.传统法通过最值点列方程求解φ，揭示了φ的本质；而对应法则根据函数y=f（x）与函数y=sinx在一个周期内图像特殊点之间一一对应的关系，结合整体思想，列出关于ω，φ的方程组求解，相比之下更为简捷、明了.

在求解三角函数图像以及性质相关问题的选择题或填空题时，在推导的严密性要求不是很高的情况下，利用对应思想，把要研究的三角函数问题对应到相应基本三角函数在一个周期内的图像上研究，思路清晰，方法简捷，既简化了问题，使学生把握了问题的本质，又提高了学生的数学素养！

三、利用换元法解三角函数题

在解某些三角函数问题时，如果直接运用三角公式运算非常复杂，或无法求解.这时不妨采用换元法，沟通题设条件与所求结果（或所证结论）的关系，运算过程就会化难为易，变繁为简，使问题顺利得到解决.

1.利用三角函数进行换元

=sinθcosφ+cosθsinφ=sin（θ+φ）≤1.

通过利用三角换元进行降次，便于用三角公式直接运算，使证题过程变得十分顺畅.

2.利用万能代换公式进行换元

例6若tanα+secα=2，求sinα的值.

通过利用万能代换公式进行换元，使三角运算转化为代数运算，使解题过程变烦琐为简洁.

四、逆向思维在解三角函数有关问题中的应用

根据思维过程的指向性，思维可分为正向思维（常规思维）和逆向思维（求异思维）.在中学数学教学中，与逆向思维紧密联系的有逆运算、逆命题、反证法、分析法和充要条件等.当一道数学题用常规思路和方法求解思维受阻而无法进行下去时，我们可以尝试寻求另一种数学思想方法，即用逆向思维的方法来探索开辟新的解题途径，往往能起到意想不到的良好效果.

1.逆运算

《三角恒等变换》中的和（差）角公式：

例7求值：（1+tan1°）（1+tan2°）…（1+tan44°）.

本题是多个因式相乘，乍一看，似乎根本无法下手.其实只要静下心来仔细观察题目的特点，会发现1°+44° =2°+43°=…=45°，而45°正好是一个特殊角，且tan45°=1，于是我们可将第一项与最后一项结合，第二项与倒数第二项结合，…，以此类推，但只做到这里，许多同学就再也进行不下去了.这些同学能想到把首尾两项相结合已经很不错了，只可惜逆向思维能力欠缺，最终导致功亏一篑.

解：因为（1+tan1°）（1+tan44°）

=1+tan1°+tan44°+tan1°tan44°

=1+tan（1°+44°）（1-tan1°tan44°）+tan1°tan44°

=1+1-tan1°tan44°+tan1°tan44°

=2.

同理可得（1+tan2°）（1+tan43°）=（1+tan3°）（1+ tan42°）=…=（1+tan22°）（1+tan23°）=2.

所以（1+tan1°）（1+tan2°）…（1+tan44°）=222.

二倍角正弦公式连续使用时要注意构造余弦的二倍角关系，类似地，可以证明恒等式cosαcos2αcos4α…

2.反证法

反证法在解题中用途十分广泛，在三角函数的证明中作用也是非同小可.

例8在△ABC中，若sinA＞sinB，则A＞B.

本题已知正弦值的大小，求与其所对应角的大小关系，我们可以根据三角函数的单调性进行求解.值得一提的是，注意自变量是否在同一个单调区间内，否则先转化再比较.

证明（反证法）：假设A≤B.

（1）若A=B，则sinA=sinB，显然矛盾，故A≠B.

所以sinA＜sinB，这与sinA＞sinB矛盾，故A＞B.

在△ABC中，A+B＜π，A＜π-B，

故sinA＜sin（π-B）=sinB，

这与sinA＞sinB矛盾，故A＞B.

反证法是中学数学的一种重要思想方法，按结论的反面是否为一个时可分为归谬法和穷举法.一般地说，当结论的反面比结论本身更简单或直接证明包含无限等问题存在困难时宜采用反证法.

总之，三角函数的三角变换涉及的公式较多，应立足课本，在掌握这些公式的内在联系及推导过程的基础上，理解并熟记这些公式，掌握公式的正用、逆用、变形用，它可以提高思维起点，缩短思维路径，从而使运算流畅自然.善于运用方程的思想，把三角函数式的化简与求值问题转化成方程问题求解.利用三角函数图象熟练掌握函数性质.