让高三复习从“解题困惑”走向“自主理解”

☉浙江省建德市新安江中学 蒋 燕

让高三复习从“解题困惑”走向“自主理解”

☉浙江省建德市新安江中学 蒋 燕

一、问题的提出

这是笔者在进行高三二轮复习“函数与零点”时的一则教学案例：

当这个例题呈现后，大部分同学都能对f（x）=f（x-1）这个条件理解到位，并借助图像，比较迅速地将y=f（x）（令a=0时）这个分段函数的图像呈现出来.很明显，一旦图像呈现出来该问题基本迎刃而解了.

图1

继而笔者给出下面变式：已知函数f（x）=-x2-x+a，且函数y=g（x）-ax恰有三个不同的零点，则实数a的取值范围是_________.

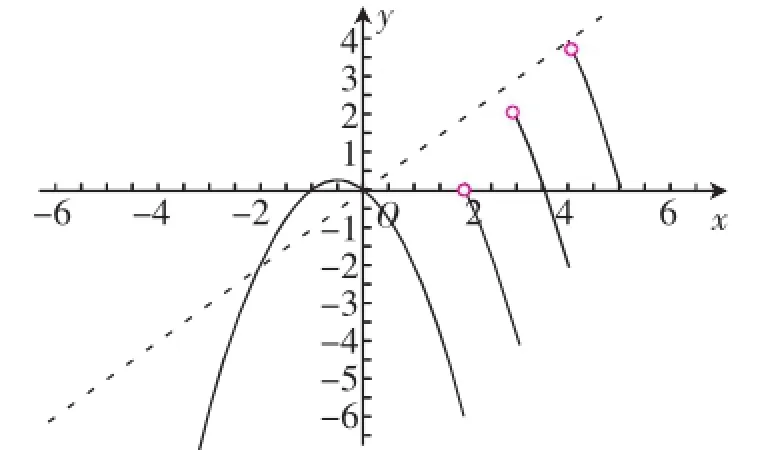
图2

同学们很快地作出了图形（图2），笔者惊讶了.

在高三的复习课堂中，教师经常看到这样的状况发生：学生没有对问题进行仔细理解与剖析、很多时候只停留在模仿阶段、也不管这个题的情境是否发生了变化，不在乎是否会出现形式上的相似掩盖了本质的不同情况，不会主动实现自身思维的突破，陷入思维定式.在这种时候，我们老师就应该思考如何及时抓住学生的困惑点并进行剖析，让学生有一种彻底领悟、通透的感觉.

二、高三二轮复习中的问题分析和策略思考

如果说高三数学一轮复习注重的是基础，那么，二轮复习注重的是如何提升学生的综合解题能力.每年的高考试题都十分注重基础与创新的有机统一，这对高三教师来说，如何指导学生透视创新的问题、化归为用常用的办法去解决它是至关重要的.

在以往的高三数学二轮复习中，多采用常规的复习模式，即：

这种复习模式面临着巨大的负担就是要做大量的练习，出现类似的问题就会、出现不同的就不会，导致高考时出现从未见识过的新题时，心态便会一下失衡.

大多数时候教师的着眼点在于如何利用本节课把学生在作业或是测试中出现的问题一一讲解完.多数时候都是采用“老师→学生”单向的被动型和灌输性的教学方法，对于学生出现的某个困惑点的针对性剖析不够精细，学生一课堂听下来，趣味索然且易疲劳走神，而且这种模式出现了一种“老师一讲我都懂，老师不讲我便不知如何下手”的尴尬境地.针对这种情况，笔者采用了“困惑式”复习模式，其复习模式的流程如下：

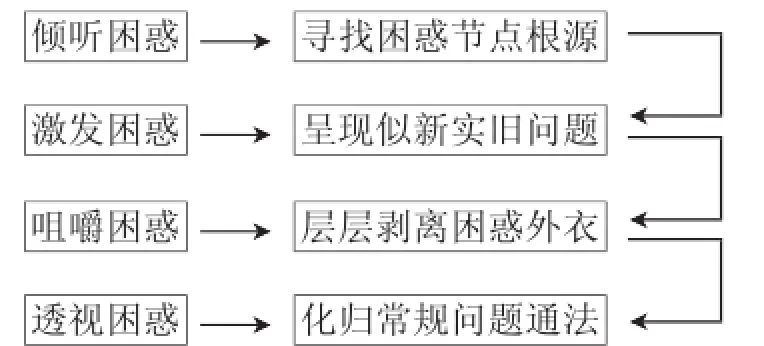
这种复习模式，课堂不再是一个单授单学的课堂，它是利用有困惑的障碍与有趣的思维进行着不断的交融、碰撞、延展的一个活动.而交融、碰撞的导火线就是困惑的存在、学生探真知的迫切欲望.有趣的困惑探索式复习教学模式可以让师生共享彼此思考，感受彼此情感，达到思维的共振，最终激发学生的学习潜能和应变创新能力.

三、“困惑式”复习模式的课堂实践和应用研究

抓住“困惑”这个瑰宝，让二轮复习课“灵动”起来.一节课下来，一天下来，一周下来，学生有他自己的思维思路，如果能顺着学生的思维发展，教师进行精心选题并讲解，必定能让学生的水平能力有实质性的提高.可是由于老师在课堂上的对象不是一个，而是一群，那怎么顺着他们的思维思路呢？最好的办法当然是顺着学生作业中存在的困惑或是测验中出现的困惑或是课堂中出现的困惑进行引导、调整、反馈、加深，才能让学生在整体上有实效性的提高.

1.“倾听”学生困惑点，寻找困惑节点根源

教科书凝聚了在数学教材研究方面造诣深厚的众多专家的心智，是一线教师平时教学的基础和根本.定义与概念的理解最省事的做法是将有关定义直接奉送给学生：“这是规定，记住它”，然后匆匆忙忙地投入解题活动.如此做法，在学生的大脑中根本不可能实现内化，不会产生“化学反应”，煮了“夹生饭”，只要题目有稍稍新颖的变化，学生脑子里就疑问成堆.这对思维发展极为不利，实际能力的提高也很有限.

案例2：设不共线的两单位向量α，β，满足α·β=0，且满足2（α-γ）·（β-γ）=|α-γ|·|β-γ|，则|γ|的最大值为_______，此时|α-γ|的值为________.

师：为什么完全动不了手？

生：题目中给的条件这个等式看不懂，不明白有什么信息.

教师震惊，为什么在教师眼中最基本的向量数量积的定义问题，在学生那成了无法突破的障碍.很多时候，教师无法理解学生为什么连这么简单的问题都无法解决，甚至一边生闷气一边批评学生的同时快速地将（αγ）与（β-γ）的夹角就是60°的结论一带而过.很明显，这样的教学会导致下一回碰到此类向量进行加减运算后的数量积情况，可能学生仍然糊里糊涂，事实上教师没有及时敏锐地抓住学生的此处困惑点.既然如此，教师是否可以帮助学生一层一层地脱去这令学生感到困惑的外衣呢？并且在平时的教学中经常使用此手段，从而让学生形成一种习惯性的思维方式之一呢？

比如说：向量作差后是一个新的向量，那可令α-γ＝m，β-γ=n，那么2m·n=|m|·|n|，显然m与n的夹角为60°，这就成功剖去了困惑的外衣的第一层；结合条件α·β=0与图象作出m与n，来确定γ，这又成功剖去了困惑的外衣的第二层.

为达成笔者设案例2之“意”，笔者营造了一个新的问题之“境”：

第一层抓住c是空间任一向量；

第二层剖去xa+yb是由a与b线性表示的任一向量，可在图形中作出.

数学问题毕竟不是洋葱，脱了一层又有一层，很多时候学生如果会脱第一层困惑的外衣，可能就已跨过了自身思维的障碍、直击问题的根源了.如果学生养成了这样的思考习惯，那当他们碰到创新问题的时候也能比较淡定的处理了.

2.“激发”学生困惑点，呈现似新实旧问题

若教师在帮助学生解决困惑时，不仅能敏锐地捕捉到学生的困惑点，并利用这个困惑点激起新的一浪又一浪的困惑，形成一条有主线的、且循序渐进的系列，这样不仅能彻底解决学生在某个知识点理解上的困惑，还能将困惑的延展区也清除干净，从而让学生体会到畅快淋漓的成就感.

案例3：如图3，已知|AC|＝|BC|＝4，∠ACB＝90°，M为BC的中点，D为以AC为直径的圆上一动点，则的最小值是_________.

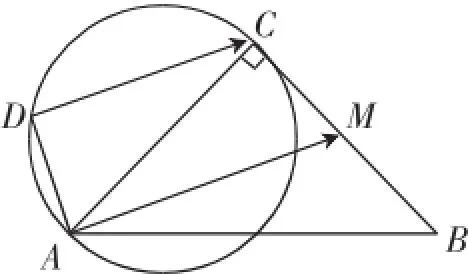
图3

这个问题在高三向量的复习中第一次出现时，重点班九成以上的学生无法完成，究其原因如下：

困惑二：向量放进“形”中总是让人害怕.

面对学生如此多的困惑点，笔者不但不及时帮助学生解惑，反而扔出一堆新问题，如：

若将图例中的所有线段看成向量，你能计算哪些向量间的数量积？

为达成笔者设案例3之“意”，笔者营造了一个新的问题之“境”：

若教师以解出问题的答案为目的，那学生对该问题只能停留在肤浅型记忆的阶段，这离我们的教学目标还很远；若教师以给出解决问题的方法为复习课的着重点，那学生对解决该类型问题的方法很有可能只停留在记忆型理解的阶段，也离我们的教学目标很远.授人以鱼不如授人以渔，很多时候教师已经授人以渔，但学生却不知何时用、何处用.如果教师在授人以渔的同时让学生养成一层一层去铺垫，一层一层去剥离复杂的问题为简单的问题的习惯思维，那“渔”自然也就能用上了.这种长久教与学的方式才会使学生体会到在自己思维里绽放的快感.

3.“咀嚼”学生困惑点，层层剖析困惑根源

教师在点拨学生的疑惑之前不仅自己要先对此问题某一个或某几个困惑点进行“咀嚼”，同时也要站在学生的思考角度进行“咀嚼”，并引导学生如何“消化”.很多时候我们教师自身也发现一个问题在一次“咀嚼”与多次“咀嚼”的情况下得到的反思结果是不一样的，深度也是不一样的.

案例4：已知数列｛an｝满足

这是2015年的浙江理科数学压轴题，这道题全省的得分平均分非常低.从该题的平均分可以看出大多数考生在考场上心中无底，困惑弥漫，信心不足，从而导致考试的不成功.

那众多人的困惑是什么呢？笔者站在学生的角度思考：是不是学生平常习惯于求通项、求等量关系，碰到不等关系不知如何下手？作差或作商在证明不等关系时是比较常用的手段，在平常的练习中也常见，在高考时学生能否结合数列用得起来呢？又或者基于要框定的范围，那能否联想到函数的值域问题，数列通项公式本质便是特殊的函数关系，而，那么只需框出an这个变量的范围即可.

透过2015年的浙江理科数学压轴题来看2016年的浙江理科数学压轴题：

（1）求证：|an|≥2n-1（|a1|-2）（n∈N*）；

题设与问题中也出现了与2015年一样的不等关系，同时还多处出现绝对值，学生的第一反应是有些胆怯的.那我们来试着剖析一下该题设：

已知这个等式，如何求an的通项公式，这是学生比较拿手的，两侧同时除以2n，得到，由这个递推关系可通过叠加法求出an的通项公式.然后再将等号改回不等号，结合上绝对值不等式不就把问题解决了吗？

其解决问题的思想方法与2016年的浙江高考题不是一回事吗？其思维习惯还是要学会一层一层地剖析问题然后非常自然地回归到常用的解题方法.

无论在生活还是学习上，剖析情景才能变通，变通常常是打破僵局的有效办法.著名数学家G.波利亚在总结解题时说：“我们必须一再地变化它，重新叙述它、变换它，直到最后成功地寻到某些有用的东西为止”.从一个“境”到另一个“境”，好似一条思维传输带，教师要让学生学会判断这条传输带上是否有东西可拿，如何摘取.这个“拿”不是简单思路的累积，更不是多做几道题就能做到，而是要拿解题的核心手段，对数学疑惑点的本质认识，对数学规律的理性认识.学生只有在不同背景中，形成了自觉运用解题手段时，才可以说真正掌握了化繁为简、剖析化归的能力.

4.“透视”学生困惑点，化归常规问题通法

比起教师在平时的课堂或是课后作业中观察出来的学生在某些问题上的困惑，那学生在测试中所展示的困惑更具有真实性与代表性.教师不单单可以掌握学生的这些困惑点，更可以透过学生在试卷上的展示看到学生答题时的情绪变化与苦恼所在.

案例5如图4，椭圆E的左、右顶点分别为A，B，左、右焦点分别为F1，F2，|AB|=4，|F1F2|=直线y=kx+m（k＞0）交椭圆于C，D两点，与线段F1F2、椭圆短轴分别交于M，N两点（M，N不重合）且|CM|=|DN|.

图4

（1）求椭圆E的方程；

（2）设直线AD，BC的斜率分别为k1，k2，求的取值范围.

该题是出现在高三二轮复习时的测验中，根据学生的作答情况我们了解到解决第一问时几乎所有学生的心情都是愉悦的，能轻易得到椭圆E的方程为

而第二问的解答，在设D（x1，y1），C（x2，y2）的前提下，一半的学生卡在了|CM|=|DN|这个条件不知怎么用.而剩下的所有学生非常一致地呈现了后，停留在此下不去了.可见测试的好处，呈现了一个集体的困惑.

笔者在剖析该问题时，透过现象“透视”出学生的困惑是该运算式子中没有出现学生心里所预期中的只含x1+x2和x1x2的格局，那心里承受能力一下子就崩溃了.

事实上，在剖析这个困惑时，笔者引入了我们解三次方程时的做法，虽说三次方程不作要求，可有些三次方程我们也能解，靠的是什么？比如：x3-3x+2=0，学生异口同声地说配凑法.那同理上式就可以配凑成：

还可以用最朴实的方法——求根公式，可知x1=-m+，代入即可.

学生恍然大悟，大悟之后更是有摩拳擦掌之势.借势笔者引进同类问题：

已知椭圆E的焦距为2，长轴的左、右端点分别为A，B，P是E上任意一点（不与A，B重合），直线PA，PB的斜率之积为

（1）求椭圆E的方程；

（2）过E的左焦点F作直线l交E于M，N两点，设直线AM，BN的斜率分别为k1，k2，求证：k1=3k2.

在高三二轮复习课的习题讲解课中，不但要总结解题中用到的“通法”或“巧法”，更要将教师或学生解题中碰壁、反思的过程一览无遗地暴露给学生，这种操作办法对学生学会用分析性思维解题、始终抓住问题的目标进行思维放射大有裨益.

著名数学教育家孙维刚老师说：“题做错了，是纠正自己对概念的片面理解或不正确的思想方法的反面教员，如果只是重做一遍，而不分析发生错误的第一层原因，第二层原因…，那么，即使这次做对了，再做类似的题目，还会出错.”所以当学生解答出现困惑点的时候，老师不应该马上去指导、纠正，要耐心地领着学生像在黑暗中寻找光明一样地去发现问题的本质.

四、“困惑式”复习模式的教学意义和实践反思

在每一次习题课中，在每一次讲解问题的过程中，教师不仅要讲述方法，更是要强调问题的本质，让学生一而再再而三地透过问题的表面去看本质，去思考.思考才有困惑，体验才有困惑，有求知欲才有困惑，有上进心才有困惑，解决了困惑才能更积极主动地去思考.有些同学在不同阶段放弃了数学，原因就是积累了太多他自认为无法解决或不愿主动去解决的困惑.纵观近几年来的高考数学试题，源于教材的常规题占据了一定的分量，高考命题的一个不变的原则就是“取材于教材，但不拘泥于教材”.教材中每一道例题、习题，很多高考题都能在教材上找到“根源”.夯实基础离不开教材，“题在书外，理在书内”.无论高考怎么考，原理肯定都在教材内. 2013浙江高考数学试题中第17题是众多考生在考后反映不太简单的一题，好多学生通过平方再构造函数求解的居多，虽能解题，但显然违背了命题的意图.绝对值与向量的模两者的不协调，若能让学生联想到如何让两者协调起来，那此问题就能利用向量的形的定义进行秒杀.这点充分体现高考以教材为本的理念，从中也暴露出我们多数教师复习过程没有将新问题与教材这个有效资源桥梁的搭建能力很好地培养起来.正如美国著名数学教育家波利亚所说：“一个专心认真备课的老师能够拿出一个有意义的但又不太复杂的题目去帮助学生挖掘问题的各个方面，使得通过这道题，就好像通过一道门户，把学生引入一个完整的理论区域.”

笔者认为数学解题的目的在于让每一道题都能发挥它应有的作用，而且通过“追问”“层层剥离”，能够做到举一反三，触类旁通.犹如2016年的浙江高考数列压轴题，初看是新题，学生困惑满腹，不能发现解题的突破口，而事实上突破口往往就是最“原生态”的解题方法.大多数所谓的创新题脱去华丽的外衣便是个常规题，作为教师要积极努力培养学生的分析性思维，始终抓住问题的目标进行思维活动.学生在运用分析性思维进行解题时，每一步等价转化都使学生明确已经做了什么，以及想做什么，有利于思维监控，从而使问题的条件与目标的距离进一步缩小，建立起条件与目标之间的实质性联系.数学教学的过程既是暴露学生亲历、体验问题与解决困惑的过程和探究知识的过程，更是学生展示聪明才智、筑成习惯性剖析能力的过程.所以说如何培养学生的习惯性剖析能力是值得我们教师去探究的.通过二轮复习，揭示其深刻性，领悟其本质性，旨在提高高三数学复习教学的有效性，让高三复习从“解题困惑”走向“自主理解”，使学生获得对数学较为全面的理解.

但是目前“困惑式”复习模式也存在着一些“困惑”.虽然教师在复习中针对每一节教材例题都会对教学方法作出一些选择，但是从“倾听学生困惑点，寻找困惑节点根源”的不同学生层次；从“激发学生困惑点，呈现似新实旧问题”的例题习题选择；从“咀嚼学生困惑点，层层剖析困惑根源”的教学方法细化；从“透视学生困惑点，化归常规问题通法”的教材处理，以及预设与生成等等问题上，应该如何做才能恰到好处的，针对不同层次的学生.课堂教学中应该怎样把握“有效复习”与“能力培养”的度才能使得不同学生得到最佳发展.要处理好这些关系，不仅要靠教师个人努力，还要依托有效的集体备课，需要大家的智慧共同来探讨：二轮复习中学生的解题困惑、素材的选择与挖掘、传统与现代教学方法有效整合、学生知识与能力和谐发展等问题.所以说高三数学二轮复习的有效教学探究需要坚持不懈的精神，需要我们在平时的教学和实践中不断地挖掘、摸索与总结，最终让我们的二轮复习更精彩、更有效.

1.江战明.识记·模仿·理解——认识向量基本定理的三个层次.数学通讯，2016年05期.

2.姚梅华.注重数学变式教学，优化学生思维品质.中学数学.2016年05期.

3.陈晓明.我教书，我写作，我快乐——我的数学论文写作背后的故事.数学通讯，2016年05期.

4.杨波.“追问”让答案更合理.中学数学教学参考. 2013年10期.

5.李广修.厘清“懂”与“会”的关系，促进学生既“懂”又“会”、中学数学教学参考，2013年06期.

6.张永杰.对“数学教学不要无原则地搞一题多解”的思考、中学数学，2016年07期.

7.孙维刚.孙维刚教育文丛：孙维刚高中数学.