发挥课本习题一题多解大作用

☉江苏省昆山中学 金巧根

发挥课本习题一题多解大作用

☉江苏省昆山中学 金巧根

教材是知识的本源，万变不离其宗.如何深入地挖掘教材，使教材为教学服务呢？我觉得应该重视教材知识，重视教材上的题目，一题多解，题尽其责，把教材的作用展现得淋漓尽致！下面例举教材几例谈谈一题多解的作用.

例1如图1，已知AD是△ABC的角平分线，且AC=2，AB=3，∠A= 60°，求AD的长.

解法一：①△ABC中，已知两边及夹角，余弦定理求出BC=；

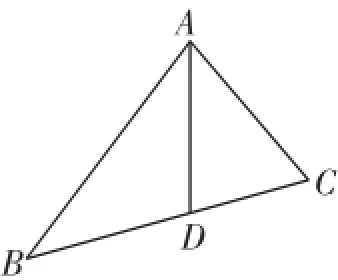
图1

评析：此方法按部就班，属于典型的通性通法，值得提倡.

解法二：①如图2，由D向AB，AC作垂线，垂足分别为E，F；设AD=x，

图2

②由等面积法知，S△ABC=S△ABD+S△ACD，

此题并没有用到所学的正、余弦定理，其中的面积公式不学这章内容也可以推导出来，巧妙地运用了等面积法，使得本来计算量很大的题目简单化，体现了思维的开拓性及知识的系统性，不被所学内容禁锢，实属妙法！

解法三：①如图3，延长AD，由B，C分别向AD及其延长线作垂线，垂足分别为E，F；

②AE=ABcos30°，AF=ACcos30°，EF=AE-AF；

图3

④AD=AF+DF.

评析：此法属于应用平面几何的知识，加上新知识——角平分线的性质对题目进行处理.

解法四：①如图4，作CE∥DA，交BA的延长线于点E；

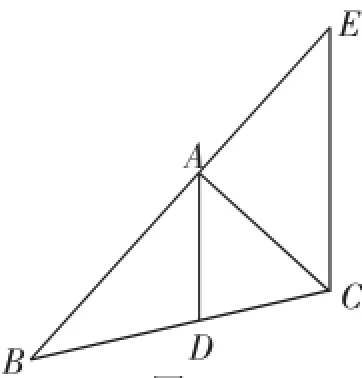
图4

③△ACE中已知两边及夹角，余弦定理求得第三边CE；

评析：此法辅助线作得很好，构造了相似三角形，只用了一次余弦定理，计算量大大减少！

评析：此法看似要用两次正弦定理，但是只需列式，不需计算，第三步两式相除后，运用角平分线的性质可知比值的大小，而不用去求这两个值，也就是只有最后一步需要代入数值计算，而且此法是完全应用本章所学知识进行解决.

解法六（学生错解）：①△ABC中，已知两边及夹角，余弦定理求出BC=；

③在△ABD中，已知两边及一对角，用余弦定理列方程组，解出两解

分析：由图5可见已知两边及一对角有两解，原题中是较小的一解；若由△ACD中用此方法解也会出现两解，由图看，应取较大的一个.所以此解法更正如下：

图5

④在△ACD中，已知两边及一对角，用余弦定理列方程组，解出两解：

评析：此法很容易出错，基础训练上的一个选择题的错误选项就是应用此法的错解得到的，加上上述更正后，虽然能做出正确答案，但是要分别在两个小三角形中应用余弦定理，计算量大，所以此法不宜使用！

例2如图6，在任意四边形ABCD中，E，F分别是AD，BC的中点.求证

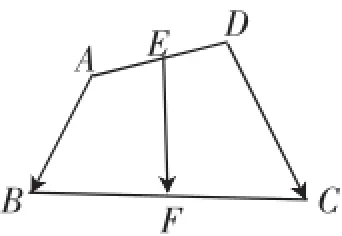
图6

在教学向量加减法的时候，引导学生探索如下证法一：

此法让学生欣赏在EF左右两侧的图形中，向量和的匀称美.

证法二：如图7，过F点作MN与AD平行且相等，F为MN的中点，则四边形AMFE和EFND为平行四边形而△BMF≌△CNF，从而得出即

图7

图8

在此法的基础上进一步引导，所要求证的结论符合运用“三角形中线向量定理”特征要求.可以通过直接将平移得到“三角形中线向量定理”的基本图形.这样就得到如下证法：

证法四：如图9，过点B作BM∥AE，过点E作EM∥AB，BM∩EM= M，则四边形ABME为平行四边形，连接MF并延长加倍至N，连接CN，EN，得到△BMF≌△CNF，进一步CN和DE平行且相等，故四边形CNED为平行四边形

图9

图9

图10

又因为F为BC的中点，所以MF为△BNC的中位线.

例3过抛物线y2=2px（p＞0）的焦点F作倾斜角为的直线，交抛物线于A，B两点，点A在x轴的上方，求的值.

评析：此方法是教参给出的方法.

解法二：设A（x1，y1），B（x2，y2），则由题意知，

因为Δ=8p2＞0，所以

评析：此方法是运用了直线和抛物线的位置关系来解决.还可以解决下面的变式题：

过抛物线y2=4x的焦点F作直线l，交抛物线于A，B两点，点A在x轴的上方，若=3，求直线l的方程.（解答略）

解法三：由抛物线的定义，可推出焦半径用直线的倾斜角θ表示的公式：

此方法是结论性的方法，可以解决高考题中的选择、填空题.在教学中，作为教师要勤于思考，潜心研究，发挥好一题多解，多题归一的教学作用，培养学生的思维发散性及主动性，进一步提升学生的思维品质，提高学生的数学素养.

一题多解及解后反思属于数学学习反思的一个重要方面.目前，学习过程中普遍存在的一种现象是“学数学=做题目”“完成作业=完成学习”，这使得学生的数学学习走入一个怪圈.学会反思或许是破解这种困局的方法之一.每当学习一个例题或完成一道习题的解答，就可以及时反思解答过程有没有遗漏，还有没有不同的方法，这道题与之前的哪个问题有联系，能否将这个问题应用到其他问题，等等.笔者通过引导学生对教材中的这道习题进行研究，不仅增加了学生探究的机会，拓展了研究空间，更让我们发现此题内涵隽永，耐人寻味，进一步领会到教材编写者的意图，挖掘出教材习题的潜在价值.在解题时既能使学生获得基本的知识和技能，也能进一步激发学生的学习兴趣，发展学生思维能力，“寻思求百通”，这才是解题“反思”的教育教学价值之根本所在.

教材是新课程标准先进理念的具体体现，是实现课程目标、实施教育教学的宝贵资源，而教材习题是教材的重要组成，在促进学生理解概念、巩固知识、形成技能、发展思维等方面有着不可替代的作用.一般情况下学生对教材习题答案的寻求不会有太大困难，使得我们忽略了对教材习题潜在价值的发掘和研究，从而浪费了很多重要的教育教学资源，这是一个必须引起高度重视的问题.教学中，教师应当学会欣赏教材，从句子品读，体微言大义；从结构品读，获教学智慧.教师应通过对教材的个性化解读，进一步领会到教材编写者的意图，从教材细微之处入手，多问为什么教材这样“说”而不是那样“说”、为什么这样安排“教学”而不是那样安排，聚焦于“微变”背后的“大义”，从而提高对数学的理解，对教材的设计理念和背后蕴含的教育价值的理解，进而才能更好地理解数学教学.