2016年高考全国乙卷第21题的解法规律及应用举例

☉湖北省武汉市黄陂区第一中学盘龙校区 李红春 刘建志

2016年高考全国乙卷第21题的解法规律及应用举例

☉湖北省武汉市黄陂区第一中学盘龙校区 李红春 刘建志

2016年高考题中，一大批优秀的试题映入眼帘，它们有的解法灵活，有的背景深刻，有的设问新颖，有的导向鲜明.全国乙卷第21题是一道推陈出新的好题，既似曾相识，又不落俗套，给人耳目一新的感觉，其解答立足通法，方法具有迁移和拓展价值，可以解决一类问题，正所谓“有物有则，触类旁通”.

一、试题及解答

题目：已知函数f（x）=（x-2）ex+a（x-1）2有两个零点.

（1）求a的取值范围；

（2）设x1，x2是f（x）的两个零点，证明：x1+x2＜2.

解答：（1）由f（x）=0，得（x-2）ex+a（x-1）2=0，

所以，当x∈（-∞，1）时，g′（x）＞0，g（x）单调递增；

当x∈（1，+∞）时，g′（x）＜0，g（x）单调递减.

问题等价于y=g（x）与直线y=a有两个交点，因此，a∈（0，+∞）.

（2）不妨设x1＜x2，由题意知，f（x1）=f（x2）=0.要证不等式成立，只需证当x1＜1＜x2时，原不等式成立即可.

令F（x）=f（1+x）-f（1-x）（x＞0），则F′（x）=f′（1+x）+ f′（1-x），于是F′（x）=x（e1+x-e1-x）.因为x＞0，所以F′（x）＞0，则F（x）＞F（0）=0，即f（1-x）＜f（1+x），则f（x2）=f（x1）=f［1-（1-x1）］＜f［1+（1-x1）］=f（2-x1），即f（x2）＜f（2-x1）.

而x2，2-x1∈（1，+∞），且f（x）在（1，+∞）上递增，

故x2＜2-x1，即x1+x2＜2.

本题第（2）问是极值点的偏移问题.以我们熟悉的二次函数为例，设x0为其极值点，若f（x1）=f（x2），则x0=但对于很多一般的极值函数，由于极值点x0左右两侧的增减速度不同，导致图像不具备对称性，在f（x1）= f（x2）时常有，我们形象地称之为极值点x0偏移了中心位置极值点偏移与高等数学中的拉格朗日中值定理存在着密切的联系.由拉格朗日中值定理，即下面的结论：

若函数f（x）满足：（1）f（x）在闭区间［a，b］上连续；（2）f（x）在开区间（a，b）内可导，则在（a，b）内至少存在一点ξ，使得f′（ξ）=

从而取ξ=a+θh，h=b-a，得f（b）-f（a）=f′（a+θh）h，0＜θ＜1.一般地，称x0=a+θh为相对于左端点a的偏移点，而θh（0＜θ＜1）则定义为偏移点相对于左端点的偏移量.可以看出，当ξ=a+θh为极值点且当时，函数f（x）的图像关于x=ξ对称.否则，函数f（x）的图像不关于x=ξ对称.就本题而言，易知x=1为极值点，在拉格朗日中值定理中取b= 1+x，a=1-x，h=2x，得到f（1+x）-f（1-x）=f′（1-x+2θx）·2x，即f（1+x）-f（1-x）=（2θ-1）x［e1+［2θ-1）x+2a］·2x.

另外，f（1+x）=（1+x-2）e1+x+a（1+x-1）2=（x-1）e1+x+ax2，

f（1-x）=（1-x-2）e1-x+a（1-x-1）2=-（1+x）e1-x+ax2.

二、规律提炼

（1）构造函数F（x）=f（x0+x）-f（x0-x）；

（2）对F（x）求导，判断导函数符号，确定F（x）单调性；

（3）结合F（0）=0判断F（x）符号，从而确定f（x0+x）与f（x0-x）的大小关系；

（4）判断f（x1）与f（2x0-x2）的大小；

三、解法应用

“一花独放不是春，百花齐放春满园”，数学解题追求立足通法，追求举一反三，触类旁通，下面再看看上述解法规律的一些精彩应用.

例1（2016年湖北省高三八校第一次联考题改编）关于函数

（1）求函数的单调区间；

（2）对于任意两个正实数x1，x2，且x2＞x1，若f（x1）= f（x2），求证：x1+x2＞4.

图1

（2）设F（x）=f（2+x）-f（2-x），x∈（0，2），

由f（x1）=f（x2），如图1，由x2＞x1知，0＜x1＜2＜x2，

于是f（x2）=f（x1）=f［2-（2-x1）］＞f［2+（2-x1）］=f（4-x1），

而0＜x1＜2，故4-x1＞2，而y=f（x）在（2，+∞）上单调递增，由f（x2）＞f（4-x1）知,x2＞4-x1，即x1+x2＞4.

点评：由第（1）问的单调性知，x=2是函数的极值点，于是构造的函数为F（x）=f（2+x）-f（2-x），先通过导数得出F（x）的单调性，注意到F（0）=0是判断F（x）符号的关键.

例2（2016年湖北省荆、荆、襄、宜七校联考）已知函数f（x）=xlnx，g（x）=

（1）记F（x）=f（x）-g（x），证明F（x）在区间（1，2）有且仅有唯一零点；

（2）记F（x）在（1，2）内实根为x0，m（x）=min｛f（x），g（x）｝，若m（x）=n（n∈R）在（1，+∞）有两个不等实根x1，x2，（x1＜x2）判断x1+x2与2x0的大小，并给出对应的证明.

如图2，设F（x）=m（x0+x）-m（x0-x），其中x∈（0，x0-1），

图2

显然φ（t）在（0，1）上单调递增，（1，+∞）上单调递减，所以φ（t）≤φ（1）=.由x0+x＞0知

由x＜x0-1，则x0-x＞1，于是ln（x0-x）＞0，

故F（′x）=1+ln（x0-x）+

故F（x）在（0，x0-1）上单调递增，于是F（x）＞F（0）=0，

即m（x0+x）＞m（x0-x），设x1＜x0＜x2，

则m（x2）=m（x1）=m［x0-（x0-x1）］＜m［x0+（x0-x1）］= m（2x0-x1），

即m（x2）＜m（2x0-x1），由x2，2x0-x1均大于x0，而m（x）在（x0，+∞）上单调递减，

故x2＞2x0-x1，即x1+x2＞2x0.

点评：这是一道分段函数的极值点偏移问题，有两点值得注意：首先，构造出的函数F（x）要注意限定自变量的范围x∈（0，x0-1）；其次，通过引入新函数φ（t）=得出其最值，再通过估算判断F′（x）的符号是一个难点.

例3（2016届湖北省七市州第三次联考题简编）已知H（x）=2lnx-ax-x2，如果x1，x2是H（x）的两个零点，H′（x）为H（x）的导数，证明：H

因为x∈（0，t），H′（x）＞0，x∈（t，+∞），H′（x）＜0，

所以H（x）在（0，t）上单调递增，在（t，+∞）上单调递减，如图3所示，设F（x）=H（t+x）-H（t-x），x∈（0，t），

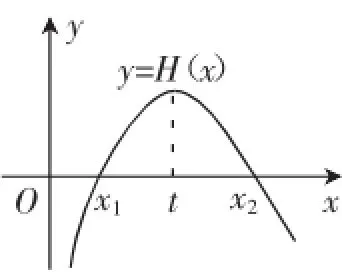
图3

F′（x）=H′（x+t）-H′（x-t）×（-1）=H′（x+t）+H′（x-t），

所以F（x）在（0，t）上单调递增，所以F（x）＞F（0）=0，故H（t+x）-H（t-x）＞0，即H（t+x）＞H（t-x）.由H（x1）=H（x2）= 0知，x1＜t＜x2，

H（x1）=H［t-（t-x1）］＜H［t+（t-x1）］=H（2t-x1），即H（x2）＜H（2t-x1），

由x2，2t-x1∈（t，+∞），则x2＞2t-x1，即因H（x）在（t，+∞）上单调递减，则x∈（t，+∞）时，H′（x）＜0，故H

评析：和前面几例比较，本题对极值点偏移的考查略显隐晦，但本质没变，以上求解的难点是要依据-2t2-at+2=0简化F′（x）=-2a，得出才能判断出导函数的符号.

总之，这类极值点偏移的不等式证明问题，其方法的精要之处在于直接比较x1与2x0-x2大小关系不便时，先比较它们的函数值f（x1）与f（2x0-x2）的大小关系，再借助单调性得出x1与2x0-x2的大小关系.