软可补子半环

袁惠淑，袁志玲，孔祥智

(江南大学理学院，江苏 无锡 213122)

软可补子半环

袁惠淑，袁志玲，孔祥智

(江南大学理学院，江苏 无锡 213122)

定义了软可补子半环的概念，研究了软可补子半环的基本性质.进一步，应用对偶软集的方法研究了软可补子半环和对偶软集之间的关系.最后，探讨了软可补子半环像与原像的性质.

软集；对偶软集；可补子半环；软可补子半环

Zadeh[1]提出的模糊集理论、Pawlak[2]提出的粗糙集理论与Atanassov[3]提出的直觉模糊集理论都是刻画不完整性和不确定性信息的数学工具.但这些数学理论都存在参数工具不足的缺陷，针对此问题，Molodstov[4]提出了软集的概念，它是一个包含模糊集、直觉模糊集、粗糙集等内涵的理论，许多学者在这方面做出大量工作.

目前，软集理论被广泛应用到数学、信息科学、计算机科学等各个领域.将软集与代数学交叉，Aktas和Cagman[5]提出了软群的新概念，并讨论了其基本性质，建立了软代数学的新研究领域.杨闻起[6]提出交换可剩余半群的剩余BCI-代数的概念，讨论其性质并给出了软半群的剩余BCI-代数，使半群的理论进一步得到充实.Ummahan等[7]把软集理论运用到环中，建立了软环理论.廖祖华等[8]在软集理论的基础上给出了软坡的概念，并进一步研究了它的一些相关性质.

半环是环概念的推广，将软集运用到半环上，得到了很多有价值的结果.丰建文等[9]提出了可补半环的概念.本文将软集理论运用到可补半环上，提出了软可补子半环的概念，并研究了它的一些基本性质.

1 预备知识

设U是初始全集，E是参数集，P(U)表示U的幂集，A⊆U.

定义1.1[10]设F：A→P(U)为映射，则称(F，A)为集合U上的软集.

定义1.2[8](软集的交) 设(F，A)，(G，B)是U上的软集.若软集(H，C)满足：

(1)C=A∩B；

(2)∀e∈C，H(e)=F(e)∩G(e).

则称(H，C)是软集(F，A)和(G，B)的交，记作(H，C)=(F，A)∩(G，B).

定义1.3[10](软集的且运算) 设(F，A)，(G，B)是U上的软集，令(H，A×B)=(F，A)∧(G，B)，其中H(α，β)=F(α)∩G(β)，∀(α，β)∈A×B.则称(H，A×B)是(F，A)与(G，B)的且运算，记为(F，A)∧(G，B).

为软集H的对偶.若A：X→P(E)为一个软集，则软集

是A对偶.

定义1.5[12]设E是一个具有二元运算“+”和“·”的非空集合，且满足条件：

(1) (E，+，0)和(E，·，1)都是幺半群；

(2) (E，+)是交换半群；

(3) ∀a，b，c∈E，(a+b)c=ac+bc和c(a+b)=ca+cb；

(4) ∀a∈E，0·a=a·0=0.

则称E为结合半环，简称半环.若E只满足条件(1)，(3)，(4)，则称E为加法非交换半环.

定理1.2[13]E是可补半环，则E是乘法幂等的，即aa=a，∀a∈E.

定理1.3[13]可补半环E必是加法和乘法可交换的.

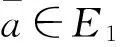
定义1.8[7](同态映射) 设E1，E2是可补半环，f：E1→E2为一个映射.称f是同态映射，若满足：

(1)f(a+b)=f(a)+f(b)，∀a，b∈E1；

(2)f(ab)=f(a)f(b)，∀a，b∈E1；

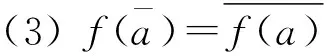
定义1.9[7](笛卡尔积)A，B是两个非空集合，记A×B为A，B的笛卡尔积，且

A×B={(x，y)|x∈A，y∈B}.

定义1.10[7](笛卡尔积的乘法运算)A，B是两个非空集合，定义A×B上的乘法运算，使得∀(x，y)，(m，n)∈A×B，(x，y)(m，n)=(xm，yn).

定义1.11[7]设E1，E2是可补半环，规定E1×E2的运算为：

(1) (x1，y1)+(x2，y2)=(x1+y1，x2+y2)，∀x1，x2∈E1，y1，y2∈E2；

(2) (x1，y1)·(x2，y2)=(x1y1，x2y2)，∀x1，x2∈E1，y1，y2∈E2；

定理1.4 设E1，E2是可补半环，则E1×E2是可补半环.

证明 易证E1×E2满足加法交换律、加法结合律、乘法结合律、乘法对加法的左右分配律.∀(x1，y1)∈E1×E2，有

(x1，y1)+(0，0)=(x1+0，y1+0)=(x1，y1)=(0+x1，0+y1)=(0，0)+(x1，y1)，

故(0，0)是加法单位元；又因为

(x1，y1)(1，1)=(x11，y11)=(x1，y1)=(1x1，1y1)=(1，1)(x1，y1)，

故(1，1)是乘法单位元；由

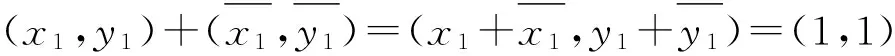
且

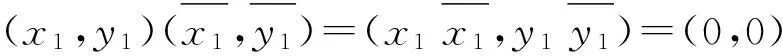
定理1.5[13]设E1，E2是可补半环E的可补子半环.若E1∩E2≠∅，则E1∩E2也是E的可补子半环.

由定义1.8的条件(3)，有如下结论.

2 软可补子半环

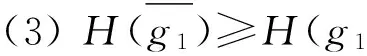
定理2.1 设E是可补半环，H：E→P(X)为一个软集.若H为E的软可补子半环，则

H(g1g2)⊇H(g1)∩H(g2)，∀g1，g2∈E，

证明 因为H是E的软可补子半环，∀g1，g2∈E，有

定理2.2 设E1，E2分别是可补半环E的可补子半环，H1，H2分别为E1，E2的软可补子半环.若E1∩E2≠∅，(H，E1∩E2)=(H1，E1)∩(H2，E2)，则H是E1∩E2的软可补子半环.

证明E1，E2是可补半环E的可补子半环，且E1∩E2≠∅，由定理1.5知E1∩E2也是E的可补子半环.∀g1，g2∈E1∩E2，

H(g1+g2)=H1(g1+g2)∩H2(g1+g2)⊇[H1(g1)∩H1(g2)]∩[H2(g1)∩H2(g2)]=

[H1(g1)∩H2(g1)]∩[H1(g2)∩H2(g2)]=H(g1)∩H(g2)，

H(g1g2)=H1(g1g2)∩H2(g1g2)⊇[H1(g1)∩H1(g2)]∩[H2(g1)∩H2(g2)]=

[H1(g1)∩H2(g1)]∩[H1(g2)∩H2(g2)]=H(g1)∩H(g2)，

从而H是E1∩E2的软可补子半环.

定理2.3 设E1，E2分别是可补半环，H1，H2分别是E1，E2的软可补子半环.令E=E1×E2，则软集(H，E)=(H1，E1)∧(H2，E2)是E的软可补子半环.

证明 因为E1，E2是可补半环，由定理1.4知E1×E2也是可补半环.∀(x，y)，(m，n)∈E，有：

H[(x，y)+(m，n)]=H(x+m，y+n)=H1(x+m)∩H2(y+n)⊇[H1(x)∩H1(m)]∩

[H2(y)∩H2(n)]=[H1(x)∩H2(y)]∩[H1(m)∩H2(n)]=H(x，y)∩H(m，n)，

H[(x，y)(m，n)]=H(xm，yn)=H1(xm)∩H2(yn)⊇[H1(x)∩H1(m)]∩[H2(y)∩

H2(n)]=[H1(x)∩H2(y)]∩[H1(m)∩H2(n)]=H(x，y)∩H(m，n)，

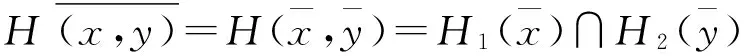
从而可知(H1，E1)∧(H2，E2)是E1×E2的软可补子半环.

定理2.4 (1)H是E的软可补子半环，当且仅当AH(x)是E的可补子半环，∀x∈X；

(2) 设A：X→P(E).则∀x∈X，A(x)是E的可补子半环，当且仅当HA是E的软可补子半环.

证明 (1) 必要性.∀g1，g2∈AH(x)，则x∈H(g1)且x∈H(g2)，所以x∈H(g1)∩H(g2).因为H是E的软可补子半环，

H(g1)∩H(g2)⊆H(g1+g2)，H(g1)∩H(g2)⊆H(g1g2)，

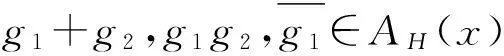
H(g1)∩H(g2)⊆H(g1+g2)；

H(g1)∩H(g2)⊆H(g1g2)；

所以H是E的软可补子半环.

(2) 必要性.一方面，∀x∈HA(g1)∩HA(g2)，g1∈A(x)，g2∈A(x).又因为A(x)是E的可补子半环，g1+g2∈A(x)，即x∈HA(g1+g2).故：

HA(g1)∩HA(g2)⊆HA(g1+g2)；

g1g2∈A(x).

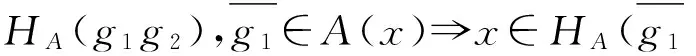
综上，HA是E的可补子半环.

综上，由定义1.7知A(x)是E的软可补子半环.

3 软可补子半环的像与原像

定义3.1[7]设E1，E2是可补半环，X是初始集合.f：E1→E2是一个映射，H1：E1→P(X)和H2：E2→P(X)是软集.定义

f-1(H2)(g1)=H2(f(g1)).

则f(H1)，f-1(H2)分别为E2，E1上的软集，称f(H1)为H1的像，f-1(H2)为H2的原像.

定理3.1 设E1，E2是可补半环，X是初始集合，f：E1→E2是一个同态映射，H1：E1→P(X)与H2：E2→P(X)为软集.则：

(1) 若H1为E1的软可补子半环，则f(H1)为E2的软可补子半环；

(2) 若H2为E2的软可补子半环，则f-1(H2)为E1的软可补子半环.

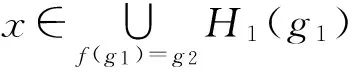
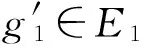
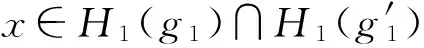
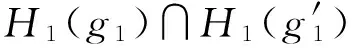
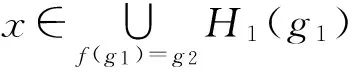
综上，f(H1)是E2的软可补子半环.

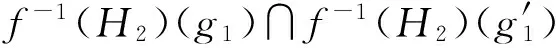
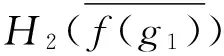
综上，f-1(H2)是E1的软可补子半环.

[1] ZADEH L A.Fuzzy sets[J].Information and Control，1965，8：338-353.

[2] PAWLAK Z.Rough sets[J].International Journal of Information Computer Science，1982，11：341-356.

[3] ASTANASSOV K.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems，1986，20：87-96.

[4] MOLODTSOV D.Soft set theory：first results[J].Computers and Mathematics with Applications，1999，37：19-32.

[5] AKTAS H，CAGMAN N.Soft sets and soft groups[J].Information science，2007，177：2726-2735.

[6] 杨闻起.交换可剩余半群的剩余BCI-代数[J].东北师大学报(自然科学版)，2015，47：22-25.

[7] UMMAHAN ACAR，FATIH KOYUNCU，BEKIR TANAY.Soft sets and soft rings[J].Computers and Mathematics with Applications，2010，11：3458-3463.

[8] 廖祖华，芮明力.软坡[J].计算机工程应用，2012(2)：30-32.

[9] 丰建文，黄福生，石定琴.可补半环[J].江西科学，2005，23(3)：207-209.

[10] MAJI P K，ROY A R.Soft set theory[J].Computers Mathematics with Applications，2003，45：555-562.

[11] 温永川.关于软集的研究[D].辽宁：辽宁师范大学，2008.

[12] 蒲保明，刘应明.不分明拓扑学Ⅰ：不分明点的邻近构造与Moore-Smith式收敛[J].四川大学学报(自然科学版)，1977(1)：31-50.

[13] 丰建文，詹棠森.可补半环上的同余[J].模糊系统与数学，2010，24(6)：61-65.

(责任编辑：李亚军)

Soft complemented subsemiring

YUAN Hui-shu，YUAN Zhi-ling，KONG Xiang-zhi

(School of Science，Jiangnan University，Wuxi 213122，China)

The concept of soft complemented subsemiring is given and some basic properties of soft complemented subsemiring are obtained.Furthermore，by adopting the dual soft sets，some properties of soft complemented subsemirings and the links with its dual soft sets are founded.Finally，the image of soft complemented subsemiring is discussed，also as the preimages.

soft sets；dual soft sets；complemented subsemiring；soft complemented subsemiring

1000-1832(2016)04-0005-05

10.16163/j.cnki.22-1123/n.2016.04.002

2015-06-14

国家自然科学基金资助项目(11371174，11301227)；江苏省自然科学基金资助项目(BK20130119).

袁惠淑(1986—)，女，硕士，主要从事模糊代数研究；袁志玲(1974—)，女，硕士，副教授，主要从事模糊代数研究；孔祥智(1971—)，男，博士，教授，主要从事模糊代数研究.

O 153 [学科代码] 110·44

A