一道经典几何题的深度挖掘*

●李玉荣

(金陵中学河西分校 江苏南京 210019)



一道经典几何题的深度挖掘*

●李玉荣

(金陵中学河西分校 江苏南京 210019)

经典几何题是重要的数学文化遗产.在数学教学和复习中，如果能重视对经典几何题的适度挖掘，即进行一题多解、一题多变等训练，那么常可获得具有探索性的问题及有价值的解法，进而能有效地训练学生思维的灵活性和深刻性，提高学生的推理能力、探究能力和创新意识．

经典几何题；变式；辅助线；一题多解

题目 在梯形ABCD中，AB∥CD，CD=AC，BD=BC，∠CBD=90°，求证：∠ADB=30°．

这是一道经典的几何题，难度不小，解题的关键是证明∠ACD=30°，辅助线的添加是解题的突破口.各种数学教辅、教参提供的经典解法如下：

证法1 如图1，作AE⊥CD于点E，BF⊥CD于点F，则

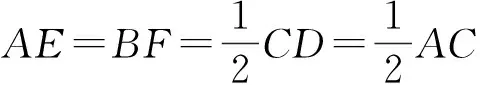
从而∠ACD=30°.由CD=AC可得∠ADC=75°，故∠ADB=30°．

点评 此解法利用梯形常作的“双高”辅助线，凸显了“通法”的解题思路，但若就此作罢，无疑于“入宝山而空返”，深度挖掘，则发现该题值得拥有和回味．

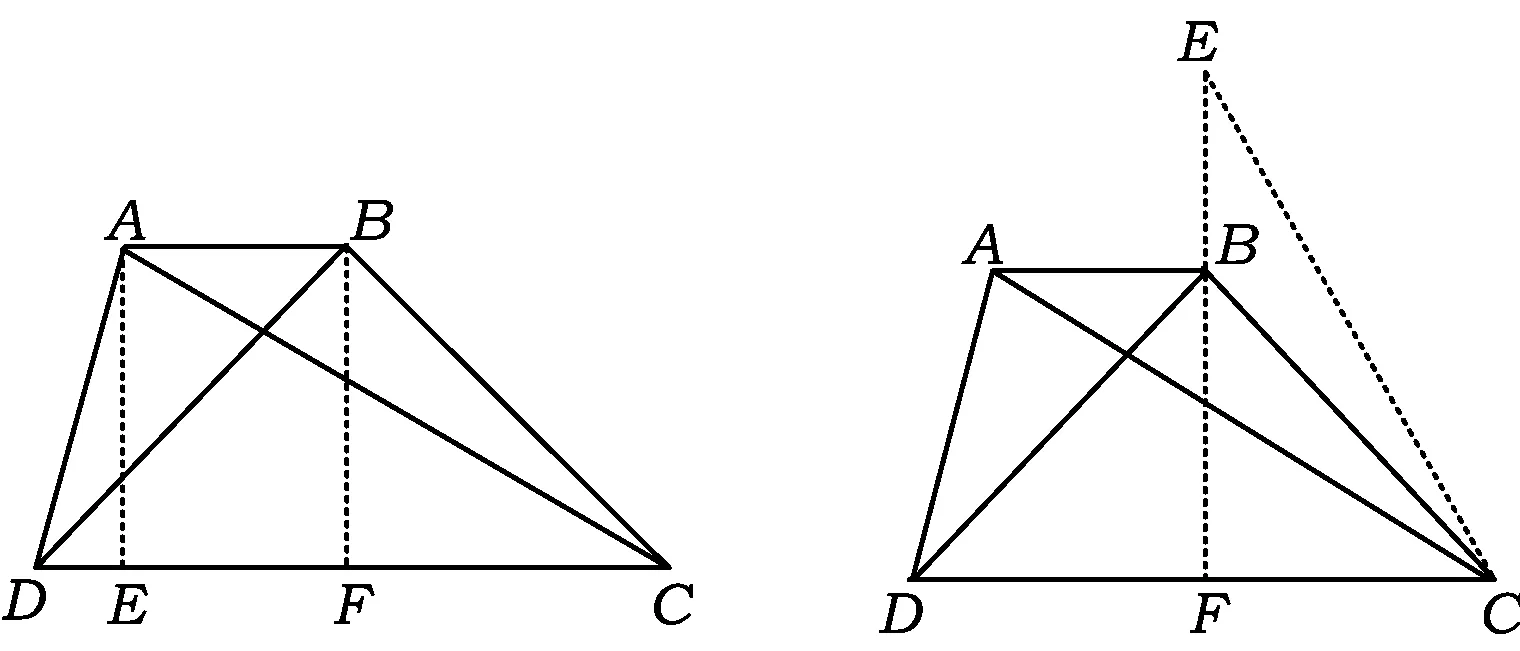
图1 图2

1 挖掘另证

证法2 如图2，将△ABC沿BC翻折得△EBC，延长EB交DC于点F，则

∠EBC=∠ABC=135°，

从而

∠ABE=90°=∠EFC，

于是

进而 ∠FEC=30°， ∠ECF=60°，

∠BCE=15°， ∠ACD=30°.

由CD=AC可知

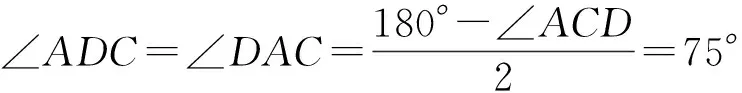
又BD=BC，∠CBD=90°，则

∠BDC=45°，

故

∠ADB=∠ADC-∠BDC=30°．

证法3 如图3，将△ABC绕点B顺时针旋转90°得△EBD，延长EB交DC于点F，则

从而

∠FED=30°，

于是

∠ACD=∠CAB=∠FED=30°，

故

∠ADC=75°， ∠ADB=30°．

评注 注意到题中的△BDC为等腰直角三角形，证法2和证法3分别利用翻折、旋转变换使分散的条件相对集中，从而顺利解决问题，较好地践行了《数学课程标准》对几何教学的新要求，凸显了图形变换的解题价值．

图3 图4

证法4 如图4，延长DA,CB交于点E，设BE=x，BD=BC=y，则

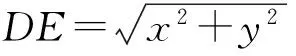
因为AB∥CD，所以

即

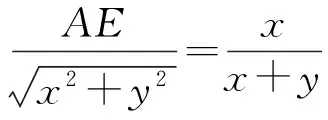
从而

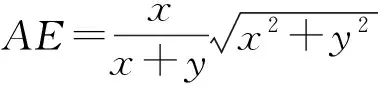
作CF⊥AD于点F，则

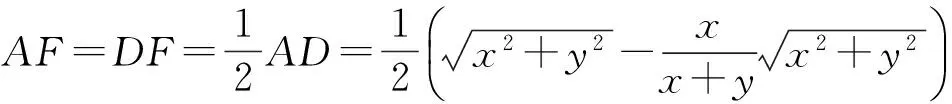
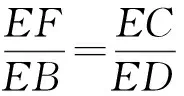
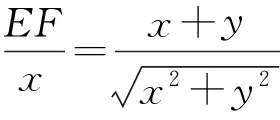
亦即

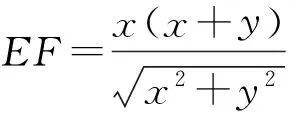
于是

化简得

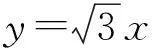
故

∠ADB=30°．

评注 此解法虽然繁琐，但“将梯形转化为三角形、作等腰三角形底边上的高”等常见辅助线的价值得以显现．

2 挖掘变式

这道经典几何题涉及5组几何元素的关系：AB∥CD，CD=AC，BD=BC，∠CBD=90°，∠ADB=30°．因此，除原题外，还可以编制出以下4道几何题，其解法更是精彩纷呈．

变式1 在四边形ABCD中，CD=AC，BD=BC，∠CBD=90°，∠ADB=30°，求证：AB∥CD．

证法1 如图5，作AE⊥CD于点E，BF⊥CD于点F.因为∠DAC=∠ADC=75°，所以∠ACD=30°，从而

故

AB∥CD．

评注 此解法沿用了原题的经典解法，顺理成章．

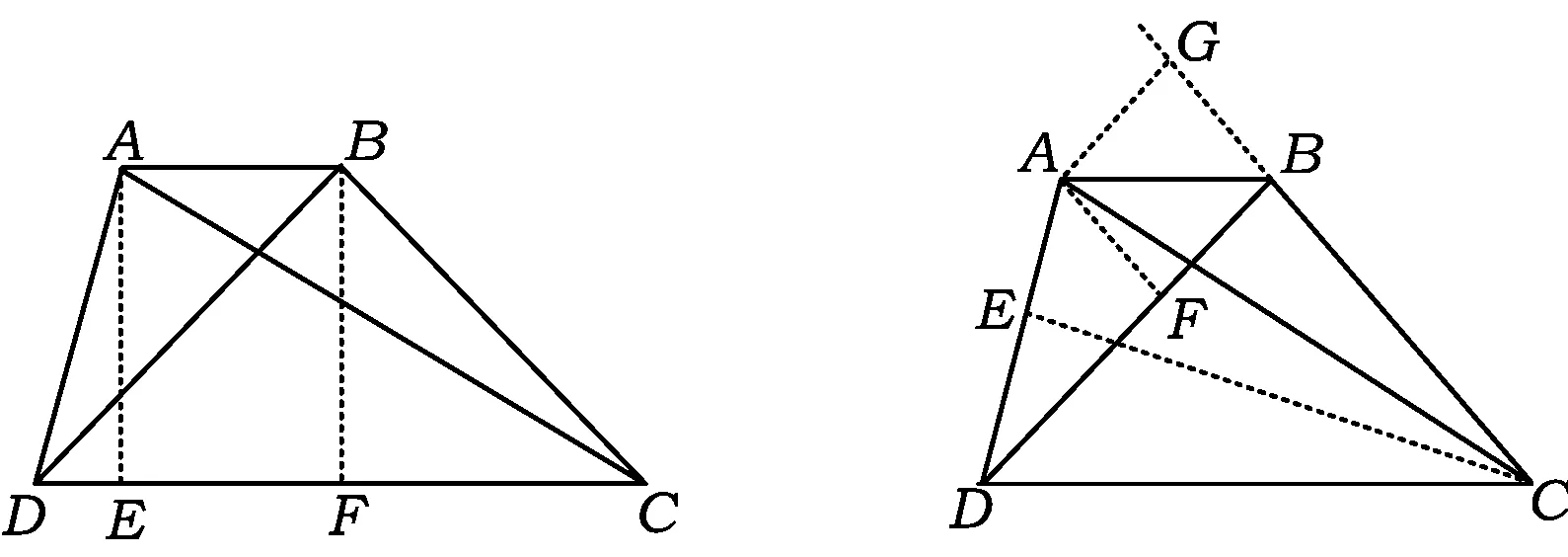
图5 图6

证法2 如图6，作AG⊥BC于点G，CE⊥AD于点E，AF⊥BD于点F，则

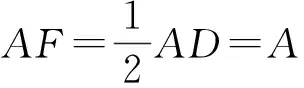
因为∠DAC=∠ADC=75°，所以

∠ACD=30°，

从而

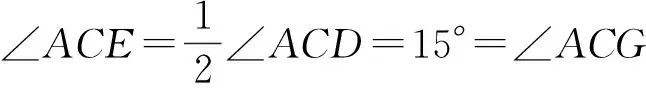
于是

AE=AG=AF，

故AB平分∠GBF.又因为∠GBF=90°，所以

∠GBA=45°=∠BCD，

故

AB∥CD．

变式2 在梯形ABCD中，AB∥CD，CD=AC，BD=BC，∠ADB=30°，求证：∠CBD=90°．

证法1 如图6，作CE⊥AD于点E，AF⊥BD于点F，则

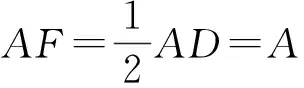
作AG⊥BC于点G，因为∠ABG=∠BCD=∠BDC=∠ABF，所以

AG=AF=AE，

从而AC平分∠ECG，得

∠GCA=∠ACE=∠DCE，

于是

∠BDC=∠BCD=3∠DCE.

又因为∠DCE+∠EDC=90°，即

∠DCE+(30°+3∠DCE)=90°，

解得

∠DCE=15°，

所以

∠BDC=∠BCD=45°，

图7

故

∠CBD=90°．

证法2 如图7，延长CA至点E，使得AE=AB，则

∠ACD=∠CAB=∠BEA+∠ABE=2∠BEA.

因为AB∥CD，所以

∠ADC+∠BAD=180°，

又∠ADC=∠CAD，∠CAD+∠EAD=180°，从而

∠BAD=∠EAD，

得

△BAD≌△EAD(SAS)，

于是ED=BD，∠ADE=∠ADB=30°，∠EDB=60°，故△EDB为等边三角形.由BE=BD=BC，知

∠BCA=∠BEA，

∠ABD=∠BDC=∠BCD=3∠BEA，

即

60°-∠BEA=3∠BEA，

解得

∠BEA=15°，

从而

∠BDC=∠BCD=45°，

故

∠CBD=90°．

变式3 在梯形ABCD中，AB∥CD，BD=BC，∠CBD=90°，∠ADB=30°，求证：CD=AC．

证法1 如图8，将△ADB沿BD翻折得△EDB，联结AE,CE，则△ADE为等边三角形.由

AE=DE， ∠EDB=∠ADB=30°，

∠EBD=∠ABD=∠BDC=45°，

知

∠EBC=45°，

从而

△EBD≌△EBC(SAS)，

于是

∠ECB=∠EDB=30°，

∠EDC=∠ECD=15°， ∠DEC=150°，

进而 ∠AEC= 360°-∠AED-∠DEC=

150°=∠DEC.

由

△AEC≌△DEC(SAS)，

得

CD=AC．

评注 也可将△BDA逆时针旋转90°得到△BCE，同证法1可证明，这里不再赘述．

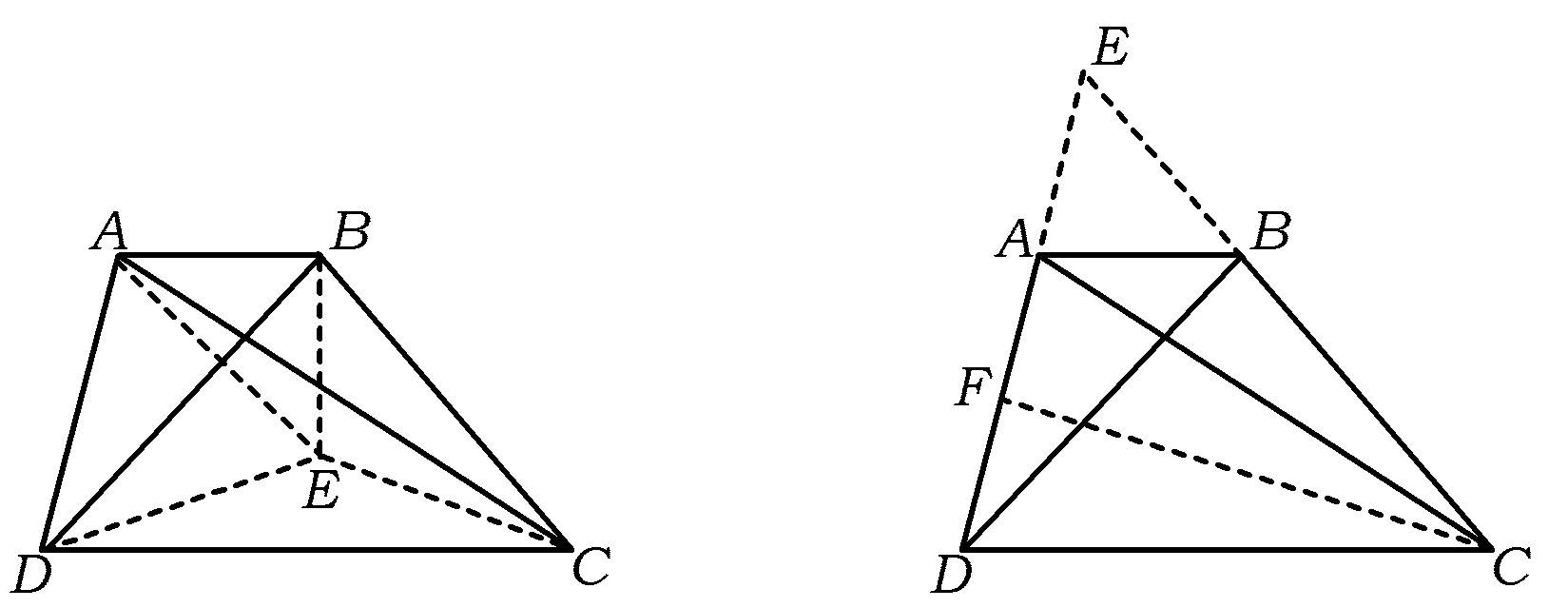
图8 图9

证法2 如图9，延长DA,CB交于点E，作CF⊥AD于F.设BE=x，则

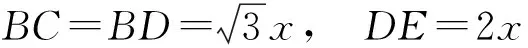
因为AB∥CD，所以

即

解得

进而

AF=DF.

又CF⊥AD，于是

CD=AC．

变式4 在梯形ABCD中，AB∥CD，CD=AC，∠CBD=90°，∠ADB=30°，求证：BD=BC．

证法1 如图10，延长DA,CB交于点E，延长AD至点F使得DF=AE，联结CF.易证△AEC≌△DFC(SAS)，从而CE=CF.又∠E=90°-∠ADB=60°，于是△FEC为等边三角形，即EF=CE.设BE=x，BC=y，则

AE=FE-DE=x+y-2x=y-x.

因为AB∥CD，所以

即

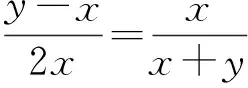
化简可得

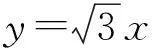
故

BD=BC．

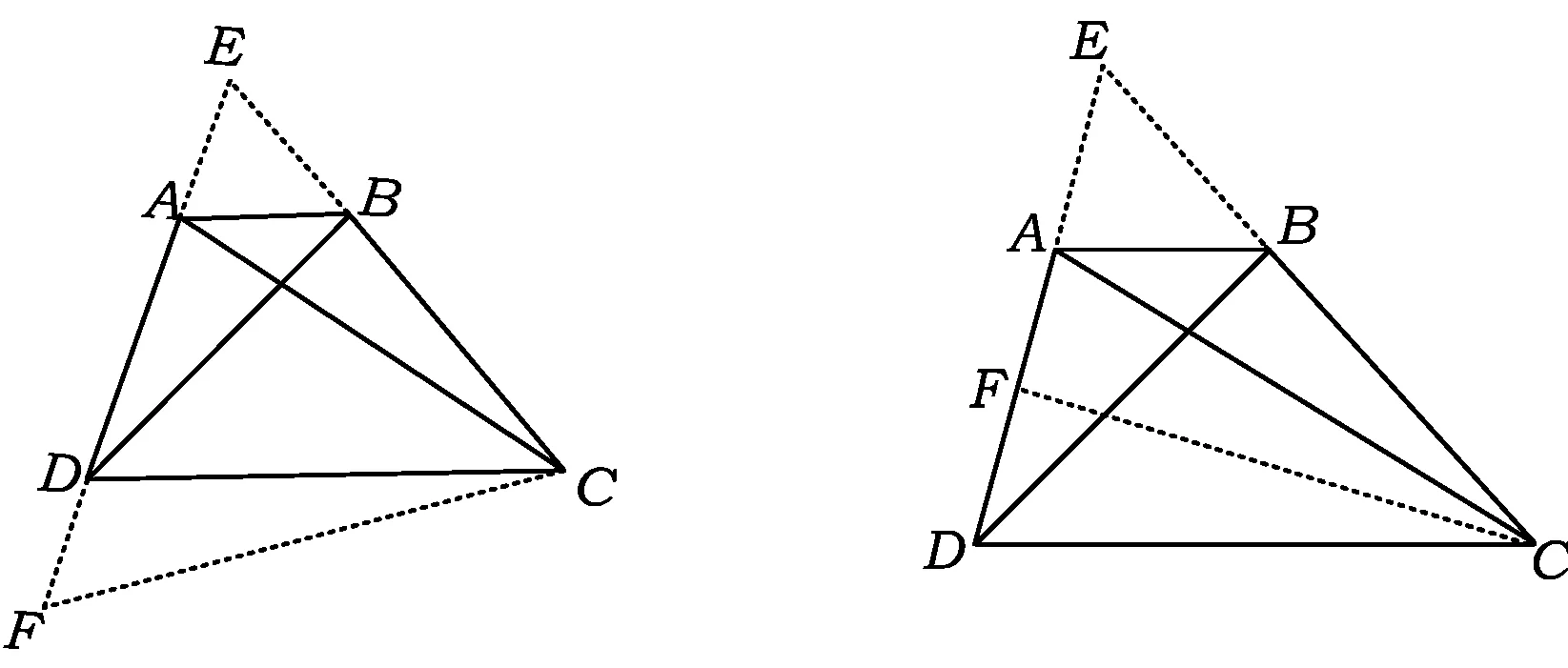
图10 图11

证法2 如图11，延长DA,CB交于点E，作CF⊥AD于点F， 则

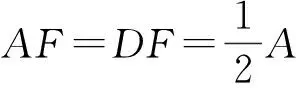
设BE=x，BC=y，则

从而

因为AB∥CD，所以

即

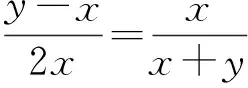
化简可得

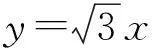
故

BD=BC．

变式1～4都有较大的难度，条件的变化引发了辅助线的变化，如何添加辅助线是解决每个问题的关键，需要解题者智慧的顿悟与迸发．“思考就有收获，挖掘定有提升”，数学的趣味性就在于它需要我们推理创造能力的充分发挥．一题多解和变式探究是增加数学趣味性的有效手段之一，解题教学需要我们聆记并践行著名数学教育家波利亚的至理名言：“一个好的教师必须理解这些，并使他的学生深刻理解到——没有任何一个题目是彻底完成了的，总还会有些事情可以做，在经过充分地研究和洞察之后，我们可以将任何解题方法加以改进，而且无论如何，我们总可以深化我们对答案的理解．”

�2016-08-04；

2016-09-13

李玉荣(1963-)，男，江苏句容人，中学高级教师.研究方向：数学教育.

O123.1

A

1003-6407(2016)11-08-04