重要的，是顺应学生的思考——试题讲评的教学实践与思考*

●傅瑞琦

(金华市教育局教研室 浙江金华 310000)



重要的，是顺应学生的思考
——试题讲评的教学实践与思考*

●傅瑞琦

(金华市教育局教研室 浙江金华 310000)

试题讲评是数学教学的重要组成部分，是数学学习的延伸和深化.文章通过“同题异构”的对比研究，探讨如何基于学生经验、顺应学生思考、设计系列问题，引导学生在观察探究、独立思考、合作交流中经历“做数学”，将思维引向深入，从而在体验中积累丰富而有效的数学活动经验.

试题讲评；经验；思考

近期，笔者所在单位组织了一次试卷讲评的教研活动,其主题是“关注活动经验，有效促进思考”，针对学生在考试时暴露出的问题，基于学生的基本活动经验来组织教学.

学生基本活动经验是课堂教学组织实施的一个基本出发点，需要从学生角度去设计学生积极参与、动手动脑的活动，引导学生在观察探究、独立思考、合作交流中经历“做数学”，从而在体验中积累丰富而有效的数学活动经验.

为了使活动能够聚焦话题，理解“学生经验”的内涵，采用“同题异构”的形式，2位教师选用同一考题，力求经过他们对教学素材不同的处理方式，产生不同的教学效果，引起听课教师的关注，通过进一步研究和探讨,寻求试题讲评教学的有效途径.1 教学素材剖析

题目 为制作一个表面积为6 cm2的正方体纸盒，现选用纸片进行如下设计，并根据图中信息，解答下列问题：

图1 图2 图3

1)方案1：如图1，圆过点A，B，C，则AB是不是该圆的直径？请判定并说明理由.

2)方案2：如图2，直角三角形纸片的2条直角边与展开图左下角的正方形2边重合，斜边经过2个正方形的顶点，求该方案的纸片利用率.

3)方案3：如图3，三角形纸片每条边均过其中2个正方形的顶点，求该方案的纸片利用率.

此题是试卷的最后一题，从整卷的解答情况看，除本题第3)小题的正确率不到1%外，其他试题均完成较好，说明学生对第3)小题所蕴含知识方法有所缺失.这是试卷讲评时需要突破的难点.另外题目中所呈现的基本图形为学生熟悉的，将圆、正方形、直角三角形等核心知识通过正方体展开图联系一起，较好地实现了知识整合,突出考查学生应用所学知识解决问题的思维过程，值得进一步研究和拓展.

2 教学片断重现

2.1 教师A的教学片断

师：根据题目可知每个小正方形的边长为1，对于方案1，说说你们的方法.

图4 图5 图6

生3：建立如图6所示的直角坐标系，得到A(-2，-1),B(2，1)，C(-1，2),因此原点O是圆心，点A与点B关于点O成中心对称，从而AB是该圆的直径.

师：对于方案1，有3位同学从不同的角度给出了3种不同的方法.下面来说说方案2求直角三角形纸片面积的方法.

生4：建立如图7所示的直角坐标系，直线EF的函数表达式为

求得E(-2，3),F(6，-1),则

AF=8，AE=4，

从而

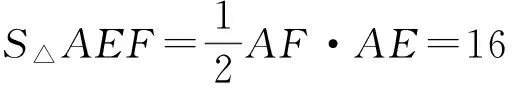
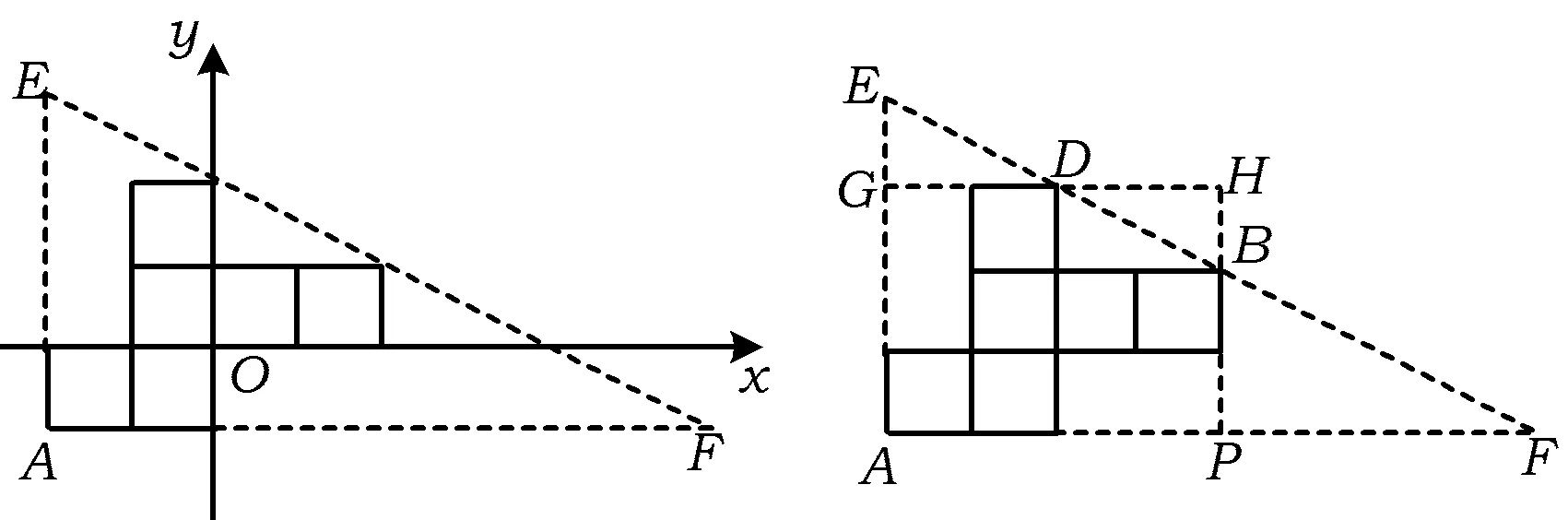
图7 图8

生5：如图8，将三角形进行分割,从而

S△AEF=S△BPF+S矩形APHG=4+12=16.

师：通过分割或建立直角坐标系就可以求出△AEF的面积.对于方案3，很多同学不会求，下面听我讲解.

接下来，教师就方案3如何求出三角形面积，利用公式求出纸片利用率，完成该题的讲解.

2.2 教师B的教学片断

想一想 第1)，2)小题的求解情况不错，但第3)小题不理想，说说解题时遇到的困难及想法.

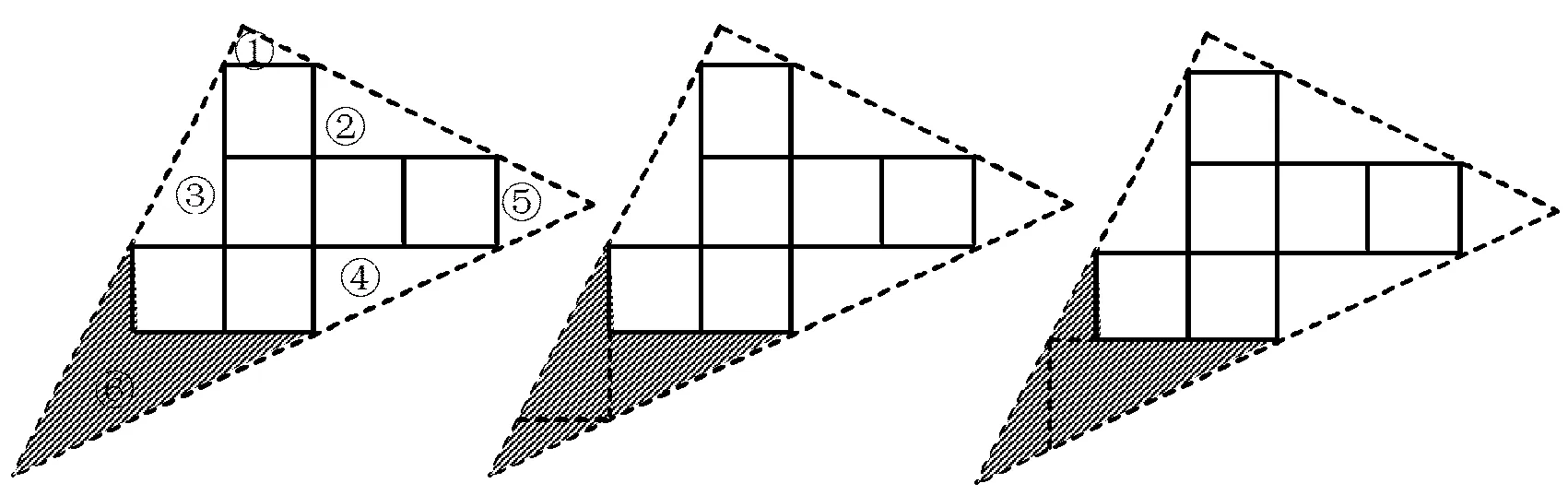
图9 图10 图11

师：请同学们观察阴影部分的图形特点，由此可以联想到什么数学知识？

生2：是一个凹四边形，有2个角的正切值为2，可以尝试将四边形分割成三角形.

师：这是2位同学用分割的方法求解时画的分割线(如图10和图11所示)，说说你的看法.

生3：分割得到的小直角三角形的2条直角边比为1∶2，但还是不会求阴影部分的面积.

师：图10和图11是在哪里分割的？

生(众)：都是在图形内部.

师：可不可以到图形外部画图呢？

画一画 你能够顺着以上2位同学的思路，继续画出图形，转化为三角形解决吗?

生4：可以画到图形外面去.如图12，设BF=x,则AB=2x,根据BC=2AB,得

1+x=2×2x,

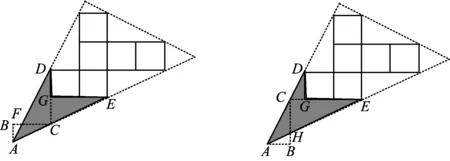
图12 图13

生5：如图13，设BH=x,则AB=2x,根据BC=2AB,得

试一试 生4和生5的方法有何共同点？其目的是什么？为什么可以这样割补？类似地，你还可以如何割补转化为方程解决？请画出图形,并进行评价.

生6：通过割补，可以得到直角三角形(图14～17)或直角梯形(图18～21)，充分利用2条直角边比为1∶2可以得出方程.

图14图15图16图17

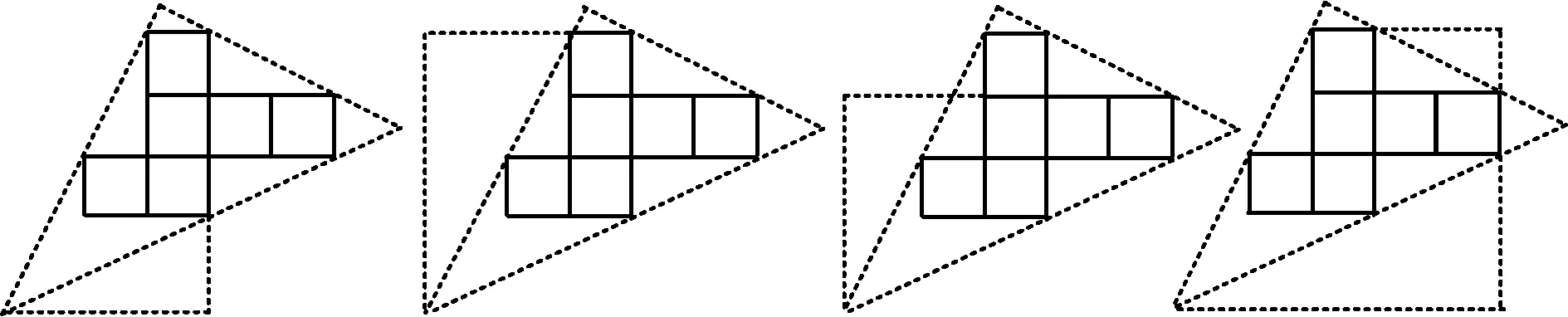
图18图19图20图21

生7：这样是可以求解，但感觉计算比较繁琐.

师：刚才的思路都是用割补的方法求凹四边形的面积，割补的目的是能够得到2条边之比为1∶2的直角三角形，从而转化为方程解决.

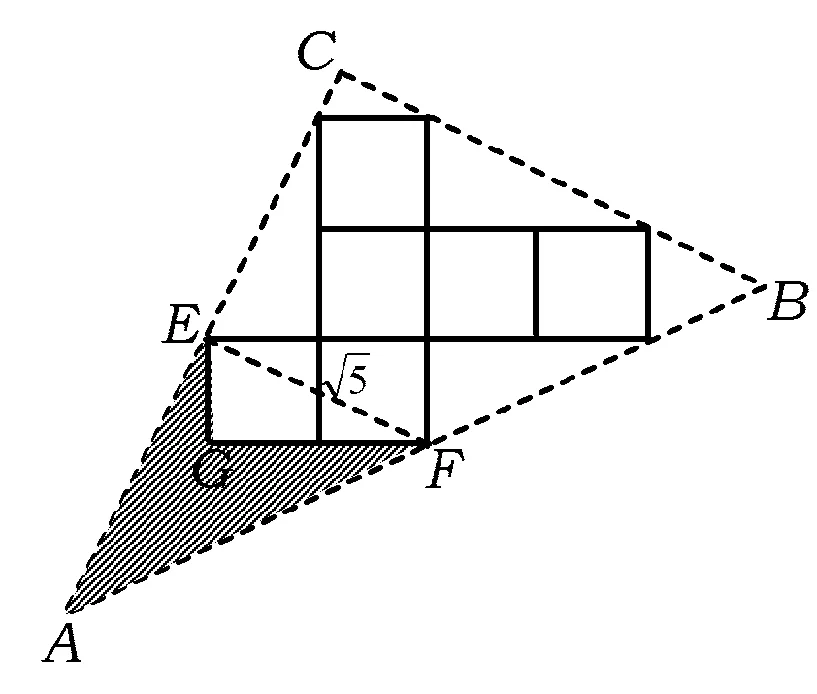
图22

看一看 如图22，有同学联结EF,这种割补的方法能求出阴影部分的面积吗？如果不能，观察图形，说说你的发现.

生8：S阴影=S△AEF-S△EFG,但△AEF的面积难求.

生9：发现EF∥BC,EF⊥AC.

生10：进一步有△AEF∽△ABC,△ABC与△AEF都是直角三角形.

师：可以求出哪些线段的长度？进一步还可以求什么？

再求△ABC的面积，比前面的方法简便.

师：发现∠C=90°后，如果求出AC就可以直接求△ABC的面积.联结EF，在求解过程中起到什么作用？这给了我们什么启发？

生12：联结EF,构造了一个与△ABC相似的三角形，利用相似比来求AC的长度.

生13：如图23，联结EP,交BC于点G,则

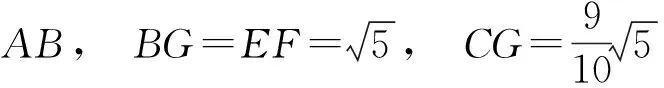
图23 图24

生14：如图24，联结DM，交AB于点H,则DH⊥AB,从而△BDH∽△ABC,于是

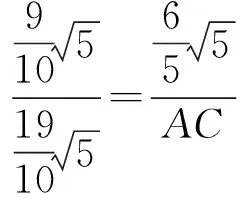
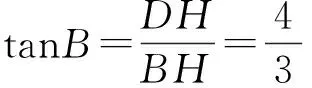
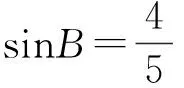
师：刚才的求解中，充分利用∠C=90°这一特点，在△ABC的内部构成相似三角形，用相似比或三角函数来求解.联系你以往的经验，利用∠C=90°这一结论，你还可以构造什么图形？

生17：如图25，作矩形AGFE,其中Rt△BCF,Rt△ACE和Rt△AGB的2条直角边比都是1∶2.设EC=x,则AE=2x,根据AG=2BG,得

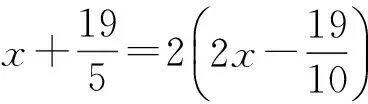
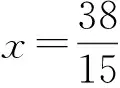
师：能否优化呢？

图25 图26

生18：如图26，设EC=x,BF=y,则

x+2y=2(2x-y),

化简得

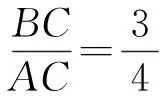
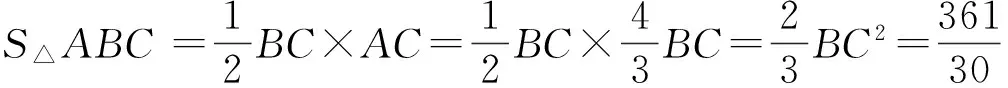
说一说 图6与图7是一位同学求前2个小题的方法，他是怎么求的？说说你的看法.

生19：建立如图6所示的直角坐标系，则A(-2，-1),B(2，1).

生20：如图7，求出直线EF的函数表达式，写出点E,F的坐标后，容易得到线段AE,AF的长度.

生21：通过建立直角坐标系，转化为求点的坐标、函数解析式来求解.

师：方案3能否用这种方法？

图27

由直线AC⊥BC,进而求得△ABC的面积.

理一理 请从图形特征、联系知识角度，总结本题的求解思路：

1)阴影部分有2个角的正切值为2，通过割补，将这2个角转化到2条直角边比为1∶2的直角三角形中，列出方程求解.

2)建立直角坐标系，求出3个点的坐标后求出三角形的边长.

3)根据∠ACB=90°，一是补全矩形利用2条直角边比1∶2，来求AC,BC的长;二是构造一对相似直角三角形，求出AC与BC的数量关系.

3 教学片段分析

3.1 重现经验，难以发展学生的数学思维

教师A组织学生充分展现方案1和方案2的解决途径，每一种方法都充分让学生交流，突出以学生为主体.但只是简单汇报各自的解法，缺少思维的聚焦、思考的连续和方法的提升.方案3是本题的难点，教师的讲解没有基于学生思考的现状，虽然能够让学生完成解题任务，但以一种告诉的形式完成教学任务，难以消除学生对本题所蕴含知识的模糊认识或错误理解，从而进一步认清知识的本质，发展数学思维.3.2 基于经验，让学生真正体会知识的发展与联系

教师B的教学，其显著特点是基于学生的经验，顺应学生的理解，引导学生进一步思考，以突破难点.“想一想”回忆方案3解题时的思维受阻、困惑之处；“画一画”“试一试”基于学生原有解题基础，引导学生到图的外面尝试画图，去发现解决问题的方法；“看一看”引导学生观察图形，从图形特点中建立知识之间的联系；“说一说”读懂同伴的解法，在同伴的思考中寻求突破难点的思路;“理一理”引导学生总结解题经验，体会其中的数学思想、研究方法，为以后的解决问题拓宽思路.通过问题引导，让学生充分经历了“反思解题—自主探究—合作交流—概括归纳”的过程，真正发挥学生生成作为教学资源的功能.

因此,教师A简单地重现知识、交流解题过程,难以发展学生的数学思维;而教师B基于学生思考经验，引导学生深入问题思考，较好地发展了学生的数学思维.

4 复习课中基于经验的实践

4.1 基于经验的教学设计

建构主义认为，学习的过程就是从已有的知识经验中生长新的知识经验的过程，是学生自我建构知识的过程.这一过程中，学生动手实践、自主探究和合作交流是重要的学习方式.

一是动手实践，巩固经验的获得.图10和图11的不成功分割往往被教师所疏忽，事实上，学生在画图和观察图形时的一些痕迹，恰恰是探索过程中的思考，应该及时地将这些直观操作转化为抽象的思维层面的经验.教师B总结“割补”转化方程解决这一途径，并进一步引导学生观察阴影部分图形特点，让学生进行“割补”画图实践，从而内化获得经验.

二是引导观察，回忆知识经验.观察图形特征找出∠C=90°后，为进一步利用面积公式求解找到方向,即构造相似求CA的长.

三是关注联系，延长思维长度.面对方案3的难点，引导学生也建立直角坐标系进行尝试，让他们体验原有解题经验的成功，让思维走得更远.

4.2 设计问题系列，有效唤醒经验

激活学生已有经验，培养学生的“理性思维”，需要学生积极地参与到每一个学习活动过程中，这就需要设置符合学生认知规律的问题系列，从而在一个不断进行问题提出、逐步探索、问题解决的过程中让学生体验、发现和归纳本题中的图形特征以及解决问题的思维方法.如“画一画”引导是让学生的视角从图形的内部延伸到外部进行尝试，轻松产生10余种割补的方法；“试一试”引导学生观察图形得出∠ACB=90°，构造相似三角形寻求求解方法，及时追问，进一步优化求解方法;“理一理”中的问题从图形特征、联系知识来总结本题的求解思路，不仅是反思解题思路，更重要的是反思思考过程，从而让数学活动经验得到提炼、总结和推广.

在一组有层次、有梯度的问题引导下，学生思维循序渐进，在不断唤醒学生经验、生成新的问题的过程中，让学生再一次巩固获得的经验，进而激活数学思维.

�2016-06-19；

2016-07-23

傅瑞琦(1966-)男，浙江金华人，中学高级教师.研究方向：数学教育.

O123.1

A

1003-6407(2016)11-41-05