一道调研试题的反思与修正*

●殷木森

(龙华新区教科研中心 广东深圳 518029) ●高贺清 (龙华中学 广东深圳 518029)



一道调研试题的反思与修正*

●殷木森

(龙华新区教科研中心 广东深圳 518029) ●高贺清 (龙华中学 广东深圳 518029)

“诊断”是高考调研考试主要的功能，而试题命制质量的高低则直接影响到诊断效果.文章呈现的是一道“解三角形”的调研试题，通过对它的解法、学生答题情况进行分析及反思，尝试从不同角度对试题加以修正，以便更好地凸显试题的考查价值.

高考数学；调研试题；解三角形

图1

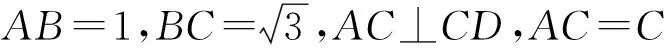
(2016年深圳市第二次调研考试数学理科第16题)

1 解法欣赏

解法1 (解三角形法)设∠ACB=α，∠ABC=β(其中β∈(0,π))，AC=a.在△ABC中，由正弦定理得

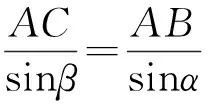
即

sinβ=a·sinα，

另由余弦定理得

a2= AB2+BC2-2AB·BCcosβ=

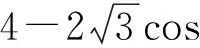
在△BCD中，由余弦定理得

BD2=BC2+CD2-2BC·CD·cos∠BCD=

评注 设∠CAB=α，在△BAD中运用余弦定理同样可求得.

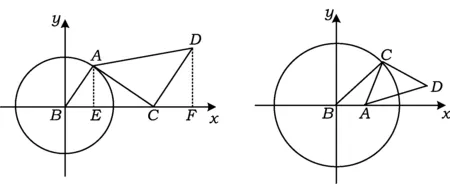
图2 图3

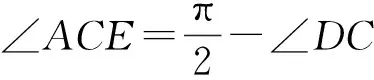
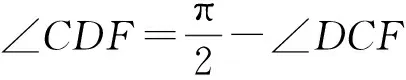
∠ACE=∠CDF.

由AC=CD，知

Rt△AEC≌Rt△CFD，

可得

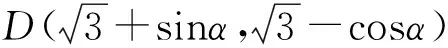
评注 以C为坐标原点、BC所在直线为x轴建立直角坐标系，然后以C为圆心、CA为半径作圆同样可求得，读者不妨一试.

即

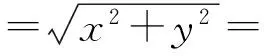
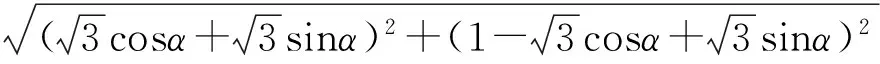
化简得

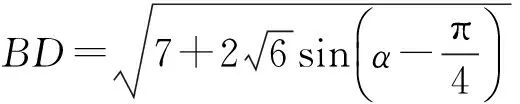
评注 运用向量法的建系方法有很多，读者也可尝试用复平面的方法进行求解.

解法4 (托勒密定理[1])若ABCD为凸四边形，则

AC·BD≤AB·CD+AD·BC.

设AC=a，因为AC=CD，AC⊥CD，所以

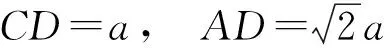
从而

即

当且仅当点A,B,C,D共圆，即∠ABC+∠ADC=π时取到等号.

这个结论也可称为“托勒密不等式”，或者“托勒密定理的推论”，大纲不作要求.

2 题目反思

如果仅从一道题目来看，这确实是一道非常精彩的题目，既可用传统解三角形的方法解决，也可用解析法、向量法，甚至运用托勒密定理一步到位.但是，全市近18 000名理科考生的平均得分只有0.09，区分度是0.06，也就是说只有300多名考生答对，其中答对的部分考生参加过竞赛培训，他们学习过托勒密定理，因此真正能运用前3种解法的考生并不多.

判断一道调研试题的好与不好，并不是看精妙的解法有多少种：1)从理论上，要看它是否符合基础性原则、科学性原则与公平性原则；2)从实际上，要看它的难度与区分度如何，一般若区分度在0.3以上的，则认为该试题能较好区分考生的能力[2]；3)再从高考命题的导向来看，看它是否能用“通性通法”解决，而不是过分强调解题技巧.显然，本题对技巧性的要求太高，一般学生不能达到，如解法1中通过sinβ=a·sinα就能把BD2表达式中的2个未知数a与α消掉，确实是太特殊化了.由于试题涉及边长与对角线，不可避免地给具有竞赛背景的考生以可乘之机，因为竞赛教程中很多有关凸四边形的结论都可以直接处理此类问题，这对其他考生而言有失公允，同时也削弱了该题作为填空压轴题的应有价值.

3 试题修正

基于上述反思，笔者认为该题可以修正为：

修正1 修改题中所给图形(如图4所示)：让BC水平放置，方便构造直角三角形，给考生指引思考方向.

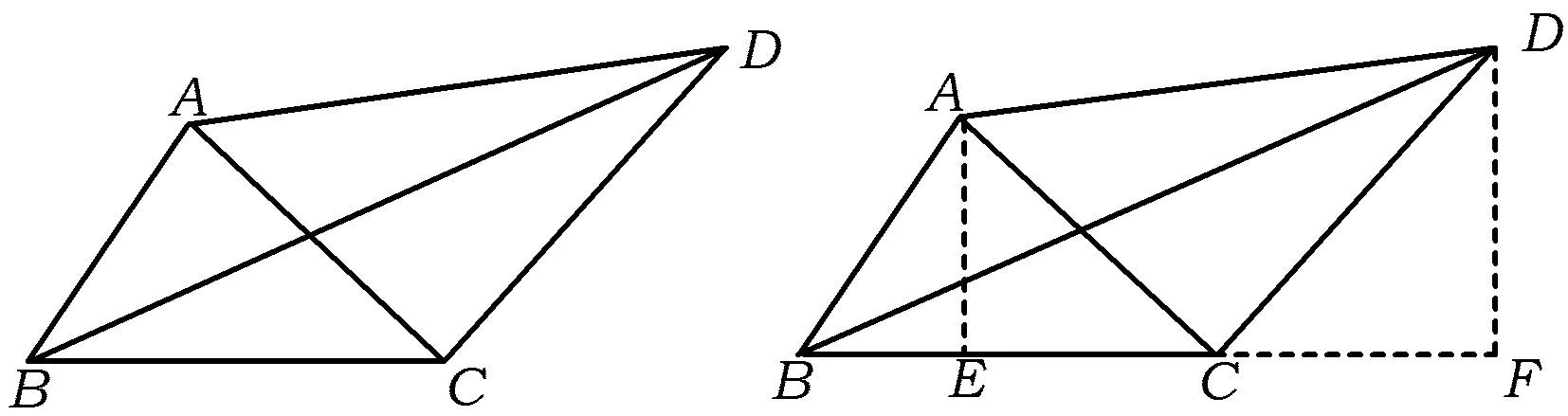
图4 图5

分析 如图5，引导学生过点A作AE⊥BC于E(点E也可能在CB的延长线上)，过点D作DF⊥BC，并交BC的延长线于点F.由解法2可知Rt△AEC≌Rt△CFD,设∠ABC=α，其中α∈(0,π)，则

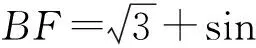
再由勾股定理得

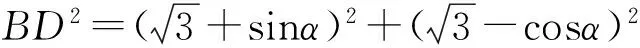
以下同解法2，不需要用到正、余弦定理就能解决.

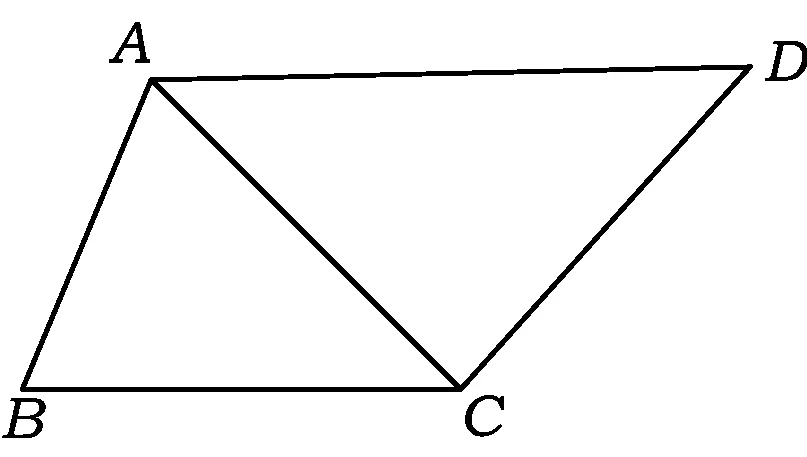
图6

分析 要求考生自主作图解答.“求四边形面积的最大值”是参考“苏教版必修5第1章第3节例4”[3]，为了便于计算，把题目中的数据也略作修改，变成一道源于课本的试题，题目的难度系数则下降了很多.具体解法如下：

解 设∠ABC=α，其中α∈(0,π)，则在△ABC中，由余弦定理得

从而四边形ABCD的面积

S=S△ABC+S△ACD=

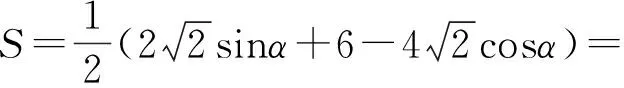
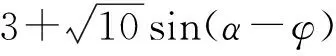
笔者又尝试对△ABC，△ACD的边角关系进行改变，但发现只要求的是对角线BD的最值范围，就不可避免地想到托勒密定理，有兴趣的读者不妨对题目再作研究，同时可以参考“2008年数学高考海南宁夏卷(文)第17题”，使它变成一道更有价值的考题.

[1] 冷岗松．奥林匹克小丛书(高中卷9)[M]．上海：华东师范大学出版社，2005：9．

[2] 殷木森．如何命制高考模拟试题[J]．教学考试(数学)，2015(4):8-11.

[3] 单墫．普通高中课程标准试验教科书·数学(必修5)[M]．南京：江苏教育出版社，2010：19-20．

�2016-07-06；

2016-09-13

殷木森(1978-)，男，广东和平人，中学高级教师.研究方向：数学教育.

O123.1

A

1003-6407(2016)11-17-03