一次阅卷中的误判*

●陈晓明

(宁国中学 安徽宁国 242399)



一次阅卷中的误判*

●陈晓明

(宁国中学 安徽宁国 242399)

一道高三周考数学试题让笔者在阅卷中引起误判，在接下来分析试卷时，笔者和学生们作了进一步探究.

误判；学习；研究；思考

这是笔者所在学校(省级示范高中)一道高三周考数学试题，笔者在阅卷中引起的误判让笔者深感羞愧，一定要加强反思，查找原因，引以为戒，避免类似事情发生．

1)求f(x)的极值；

2)若当x∈[1,e]时(其中e为自然对数的底数)，f(x)<0，求a的范围．

命题者提供的参考答案如下：

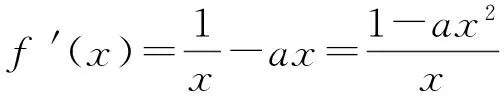
①当a≤0时，f′(x)>0，此时f(x)只有单调递增区间(0,+∞)，因此f(x)无极值．

2)解法1 (直接法：分类讨论)由第1)小题知①当a≤0时，f(x)在[1,e]上为增函数，从而

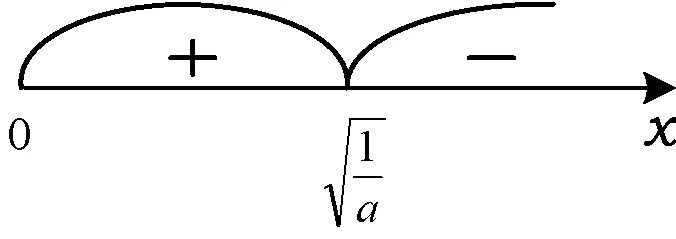
图1

与题意不符，故这种情况不存在．

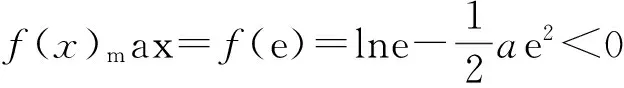
从而

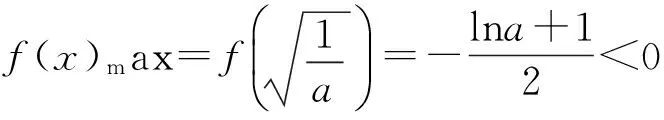
从而

即

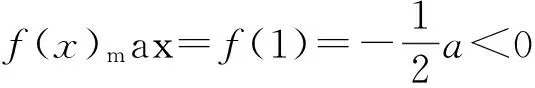
从而

a>0，

于是

a≥1.

笔者阅卷时，碰到了下面的解法(来自于班上成绩优秀的学生A)．

学生A的错误解法 1)当a≤0时，同解法1．2)当a>0时，如图1所示，f(x)在区间(0,+∞)上只有极大值

即

解得

故

随后笔者和同事们交流对周考试卷的评价和意见，笔者介绍了学生A的解法，同事认为这种解法是错误的，笔者立即问：为什么，他说：条件加强了．于是笔者开始深入研究起来．

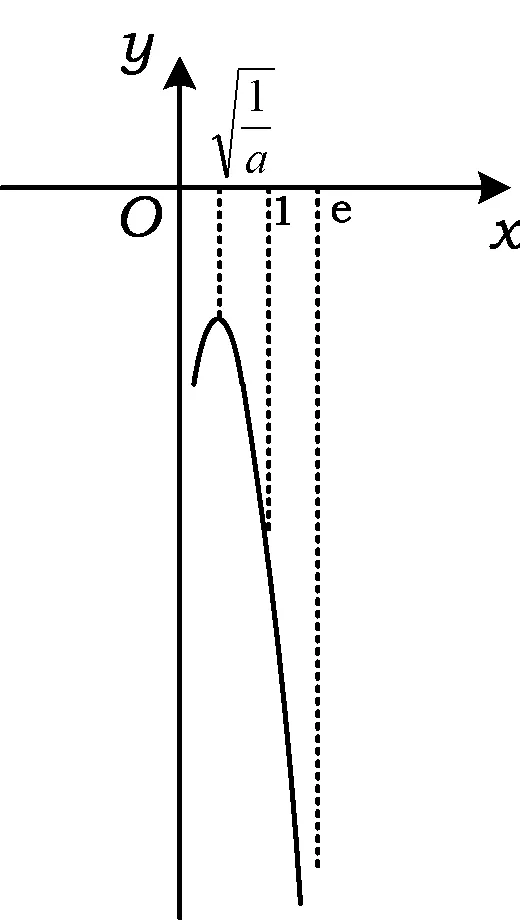
图2

那为什么学生A的解法求出的答案正确呢？是巧合吗？

为了进一步理清问题，笔者又找了一个类似的问题进行研究．

例2 已知二次函数f(x)=-x2+2ax-4在[1,2]上满足f(x)<0恒成立，求a的范围．

正确解法 (类比解法1，分类讨论)二次函数的对称轴为x=a．

1)当a≤1时(如图3),

f(x)max=f(1)=-1+2a-4<0,

解得

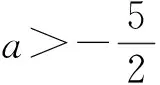
故

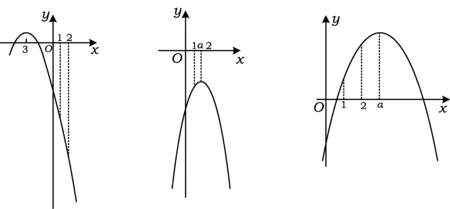
图3图4图5

2)当1

f(x)max=f(a)=a2-4<0,

解得

-2

故

1

3)当a≥2时(如图5),

f(x)max=f(2)=4a-8<0,

解得a<2，这与a≥2矛盾，故这种情况不存在．

错误解法 (类比解法3)f(x)=-x2+2ax-4在[1,2]上的最大值只可能为f(1)，f(2)或f(a)，因此只需

即

解得

故

-2

这样2种解法答案就不一样了，后一种解法是错误的，将条件加强了，从而求出的范围缩小了．为什么对于前面提到的一次函数可以呢?因为一次函数f(x)=kx+1在区间[a,b]上是单调的，而且f(a)，f(b)都存在，f(x)在[a,b]上的最大值必然在f(a)或f(b)中产生．

这件事给了笔者很大的触动：如果不和同事交流，自己又不去研究，那不就误人子弟了！看来，当老师不是一件容易的事，更不是一件随意的事，看到答案对的就误以为对的，那是不负责任的行为，很容易犯错．要当一名好老师，确实需要不断学习、研究、思考．上海市七宝中学的文卫星老师讲得很对：“一个人在事业上能走多远，取决于他的学习能力和是否能持之以恒．笔者学习的主要渠道是阅读书报杂志、向同行学习并争取与之切磋交流、与学生交流反思．”[1]笔者觉得自己应该以文老师为榜样，加强学习与研究.

陶哲轩在《解题·成长·快乐》序言中引用古希腊哲学家普罗克洛斯的话：“这，就是数学：她提醒你灵魂有不可见的形态；她赋予自己的发现以生命；她唤醒悟性,澄清思维；她照亮了我们内心的思想；她涤尽我们有生以来的蒙昧与无知……”[2]在数学学习和教学中，让我们永远带着探寻的目光审视眼前的一切，一定会有惊喜出现！

[1] 文卫星．勤于学习思考，不断实践创新[J]．中学数学教学参考，2016(4)：66．

[2] 张晓东．说题与数学青年教师的专业成长[J]．中学数学教学参考，2015(3)：67．

�2016-08-22；

2016-09-23

陈晓明(1971-)，安徽广德人，男，中学高级教师.研究方向：数学教育.

O122.1

A

1003-6407(2016)11-11-03