探寻多元思维方法，彰显学生“质疑”魅力*

☉浙江省黄岩中学　黄仙萍

探寻多元思维方法，彰显学生“质疑”魅力*

☉浙江省黄岩中学黄仙萍

现行的高考体制已经搭建了异常激烈的竞争平台，部分学生已经陷入漫无边际的“题海战术”之中，无暇顾及信息资源的深入探究与思考，更无时间主动发现问题和提出问题；部分教师为了完成所谓的教学进度，不知不觉中实施着“满堂灌”的教学方法，忽视了学生对主体知识与规律的探究过程，同时也扼杀了学生质疑的机会；解题是高中数学学习的主要活动，问题主要来源于课本教材、教辅资料和教师提问，学生过分迷信教师和资料的权威，即使意识研究对象存在问题时，也容易怀疑自己的判断能力，不敢提出自己的见解、产生质疑；笔者在本文中从实际案例的分析出发，借助于不同的思维方法，鼓励学生尝试发现问题、提出问题及解决问题，以期提升学生的探究能力、质疑能力和创新思维能力，以飨读者.

一、有机整合“条件与结论”的思维方法，让学生“质疑”

数学问题的题设条件与结论在整合过程中呈现多样性、灵活性和价值性特征，整合的具体表现为：①判断原命题的逆、否命题是否正确；②判断在改变题设条件后新命题是否成立；③对一题多解或多题一解的探究；④整合类型、结构、方法相似的变式题.

例1在平面直角坐标系xOy中存在直径为2的半圆O，如图1所示，B为半圆上任意一点，OA=2，以AB为边在△AOB外侧作等边△ABC，试求：当B点处于何位置，四边形OACB的面积最大？

教师：请同学们思考，改变题设条件信息能否构建新的问题？（如：等边△ABC性质或位置、动点B的位置……）

图1

生1：仅将题设中“外侧”→“内侧”，试求：四边形OACB面积的最大值？

生2：仅将等边△ABC变为直角三角形且∠C=90°，试求：四边形OACB面积的最大值？

生3：将等边△ABC改为正方形ABCD，试求：五边形OADCB的最大面积？

生4：在其他条件不变的情况下，在半圆上是否存在一点B，使得直线OC成为∠AOB的角平分线？

生5：在其他条件不变的情况下，在半圆上是否存在一点B，使得AB=OC或者OC长度最大？

在上述教学实践中，我们不难发现：学生的思维活动具有分析性、创造性和实践性特征；学生1、2、3的问题处理起来相对容易些，学生4和5提出的问题存在一定的难度，在课堂上让学生进行小组讨论、协作交流、教师点拨等方式，其中某一小组汇报生5问题的解法：根据题意，可令A（2，0）、B（cosα，sinα）则=（2-cosα，-sinα），60°）］2=5+4sin（α-30°），当α=120°时，取最大值且则5-4cosα=5+4sin（α-30°），即，即α=150°.

评析：在教师的引导下，学生自主参与观察、思考、分析，从而产生“质疑”（课本教材中没有的观念或结论）.实践表明，在探究新问题处理方法的过程中，即使是细微的发现也使得学生获得内心的愉悦，极大地激发了学生探究问题的积极性和兴趣，进而促进学生“质疑”能力的提升.

二、灵活运用“归纳、类比、联想”的思维方法，让学生“质疑”

在高中数学中，归纳和类比两种思维方法都具有创造性特征；由特殊推导至一般即为归纳，根据两个研究对象某一方面的相似推理至其他方面也有类似之处的方法即为类比；通过合情推理得到的结论成为新研究的起点，有助于学生发现问题和提出问题即“质疑”；由某一概念引发其他相关概念的思维方法即为联想，相对于类比而言，具有自由性、活跃性和发散性特征.

例2已知在抛物线y2=2px（p>0）上存在两个不同点A和B，O为抛物线的顶点，|OA|=|OB|，试求证：A和B两点关于x轴对称.

教师：本题是以抛物线为探究的对象，同学们是否可以借助于不同的思维方法（归纳、类比、联想……）构建新的命题？

生6：采用类比的方法，将抛物线改变为椭圆，构建新命题：A为椭圆（a>b>0）的上顶点，过A点作两条直线l1和l2交椭圆于B、C两点，且满足|AB|=|AC|，试求证：B和C两点关于y轴对称.

证明：令A（0，b），B（x1，y1），C（x2，y2），代入椭圆方程，结合|AB|=|AC|联立表达式并化简后可得（y1-y2）·

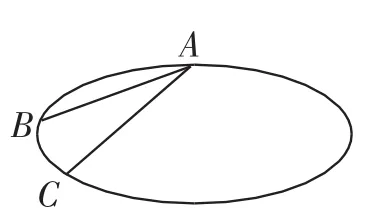
图2

教师：（生7）观察能力很强，敢于“质疑”的精神可嘉，是我们学习的榜样！我们是否可以增加些限制条件，让该命题成为真命题？

生8：由于y1+y2≥-2b，若满足<-2b，即b>c时，则添加的限制条件b>c，即可成为真命题.

评析：在传统的高中数学课堂教学中，学生处于“被动接受→机械储存→重复再现”的学习模式，缺乏观察、发现、提出问题的过程；然而，这类“归纳、类比、联想”创造性思维方法的运用，能够让学生“质疑”，进而有效建立概念、探讨方法、理解性质，提升综合素质与能力.

三、有效突显“一般与特殊”的思维方法，让学生“质疑”

在处理高中数学问题中，由特殊过渡至一般能够提供分析问题的方向，采用一般化的思维方法进行“质疑”，源于已有的问题和结论之上；采用特殊化的思维方法进行“质疑”，通常存在一般问题的特殊化和否定性结论的肯定化两种类型.

教师：同学生思考能否将题中问题进行一般化的处理，构建新命题？如何证明？

生9：将题设中椭圆的上顶点改成椭圆上任意一点，构建新命题：椭圆上不存在互相平行的两条弦（与坐标轴垂直情况除外）有同一条垂直平分线（如图3所示）.可以采取反证法证明，问题转化为中点弦问题，采取“点差法”进行处理.（过程省略）

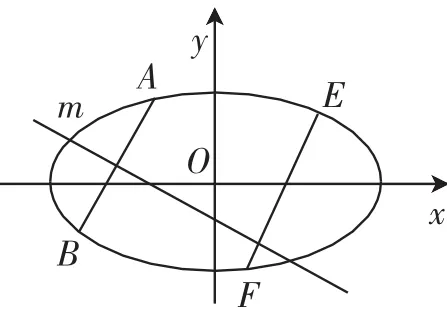
图3

例4函数y=f（x）对于任意实数存在f（x+y）+f（x-y）= 2f（x）cosy且f（0）=0，试猜想函数f（x）具有的“性质特点”，对猜想结论加以说明.

生10：函数f（x）=sinx满足题设条件，猜想性质特点：①f（x）是奇函数；②f（x）是周期函数；④∀x∈R，|f（x）|≤1；⑤f（x）在］上是增函数.

生11：令x=0，即f（y）+f（-y）=2·f（0）cosy=0，即f（-y）= -f（y），则①成立；令y=即f（x+2π）=f（x），则②成立.

生12：函数f（x）=0满足题设条件，则③和⑤不成立；函数f（x）=3sinx也满足条件，最大值为3，则④不成立.

评析：例3中引导学生利用一般化的思维方法进行“质疑”，有助于数学问题的深化理解，领悟问题的本质；例4中引导学生利用特殊化的思维方法进行“质疑”，有助于学生获取解决问题的有效途径和方法，进一步提升学生发现问题、提出问题和解决问题的综合能力.

总而言之，在高中数学学习中，质疑是学生有效学习的一种独特方式，在培养学生创新思维能力方面的功效不可小觑，正所谓：提出问题比解决问题更难；的确如此，作为高中数学教师更新教育观念，尽可能地营造数学探究性学习的氛围，不断鼓励学生大胆“质疑”，灵活运用多种思维方法培养学生的“质疑”能力，进而推动新课改的不断深化发展.F

*本文系2016年度台州市规划重点研究课题《结构观下学生数学提问能力的培养研究》（编号：TZ16046）的阶段性研究成果.