在一场“算”宴中求简明道——2016年江苏省苏锡常镇高三一模试题运算分析

☉江苏省常熟市教育局教学研究室　陈志江

在一场“算”宴中求简明道——2016年江苏省苏锡常镇高三一模试题运算分析

☉江苏省常熟市教育局教学研究室陈志江

运算是指在运算律的指导下对具体的数、式进行变形演绎的过程，运算能力是数学的三大基本能力之一（运算能力、空间想象能力、逻辑思维能力），我国基础教育数学课程一直将运算作为其主要内容.目前虽然教学中大家都很重视运算能力的培养，但是学生运算差的问题却依然存在，甚至还很突出.2016年江苏省苏锡常镇高三一模四市联考落下帷幕，绝大部分学生反映来不及做，因为有很多中档题运算量大.本次考试可谓是一场“算”宴，回顾学生运算中的不足与错误，细细分析，我们发现学生的求“简”意识不够，如果能把这些教训化成以后解题的经验，那就在失败中成长了.笔者曾在文1中对备课组长提出进行考试分析的建议，本文是从“运算”角度进行分析的一例，求“简”的数学观念是一个永恒的话题，而在运算中如何求“简”，本文试图通过具体题目的解答分析来作点探究，在此与同行探讨.

一、在用图中求“简”

数学家华罗庚曾说：“数缺形时少直观，形缺数时难入微.”数学解题中如果我们能有效地利用图形，回避运算，特别是考试中，就可以简捷地把问题处理好，会大大节省时间.

解析：设点M（x0，y0），可得B（0，y0）和直线MA的方程y-y0=-（x-x0），将直线MA的方程与直线y=x联立可解得.由点M在函数的图像上，可得从而M■→A·M■→B=-2.

尽管本题难度不是很大，大部分同学都能解出（全市实测难度系数为0.84），但求解中涉及求直线方程、两直线交点、向量的坐标表示、向量数量积运算、代换消元等运算，还是有一定的运算量.不少学生最后求得结果为2，运算出错，可谓前功尽弃，即使求对，也花了不少时间.当然有很多同学注意到点M的任意性，采用了特殊化的方法，简化运算，取点M为（2，4），则B（0，4），然后仿上过程计算得A（3，3），再求出M■→A·M■→B的结果，但仍有一定计算量.本题如果学生熟悉函数图像（如图1），从图形入手，利用直线MA与直线y=x垂直，取点M（2，4）后即可观察得A（3，3），再求出M■→A·M■→B，那么本题即可“秒杀”.

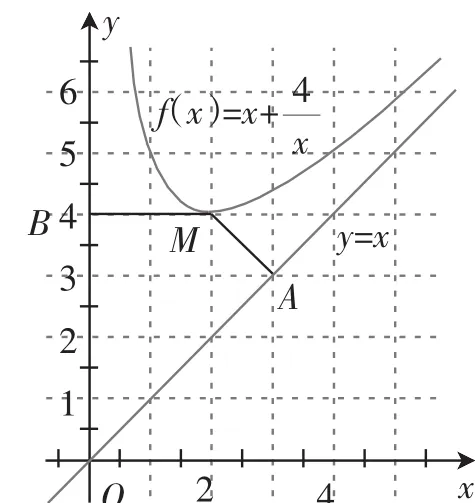
图1

例2（第10题）若一个钝角三角形的三内角成等差数列，且最大边与最小边之比为m，则实数m的取值范围是_____.

分析：本题考查正弦定理或余弦定理、不等式相关基础知识等，学生得分并不理想（难度系数为0.52），绝大部分同学都是走运算一条路.

解法1：不妨设角A，B，C从小到大成等差数列，其对应边依次为a，b，c，则B=60°.若用正弦定理做，则），可得m∈（2，+∞）.

解题中不少学生由于角A的范围出错而出现各种各样的错误答案.

解法3：同样本题若能有效用图（如图2），则观察即可得答案，当C=90°时，m=2，由于是钝角三角形，故C> 90°，这样C点向B点移动，那么就增大了，故可得m∈（2，+∞）.

图2

二、在引元中求“简”

动态问题是考试中的热点，往往需要引入变量，我们要在客观分析动因的基础上，找准问题的切入点，要把引入变量与后续运算联系起来思考，对运算过程的繁简有一个透视，只有这样才能简化求解.

例3（第11题）已知过原点的动直线l与圆C：x2+y2-6x+5=0相交于不同的两点A、B，若A恰为线段OB的中点，则圆心C到直线l的距离为________.

分析：本题引入变量主要有两种方法：一为直线l的斜率k，二是点A（或B）的坐标.

解法1：设动直线l为y=kx，代入圆方程得（1+k2）x2-6x+5=0，由A恰为线段OB的中点，知xB=2xA，用求根公式求得xA、xB，代入得关于k的方程，算得，再求得圆心C（3，0）到直线l的距离为

解法2：设点A（x0，y0），则点B（2x0，2y0），代入圆方程可得从而圆心C（3，0）到直线l：y的距离为

比较两种解法，思路都较简单，但运算量不同.解法1尽管只引入一个变量，但运算过程长，且运算式子明显比解法2复杂，容易算错，究其原因还在于引入的变量为直线斜率，导致后续必须要进行解交点坐标的运算和解关于k的方程xB=2xA；而解法2虽然引入的是两个变量，但充分利用了中点和点A、B都在圆上的条件，在解A点坐标时大大减少了运算，使解题更加快捷.

（2）设直线l与椭圆C交于A、B两点.

①若直线l过椭圆C的右焦点，记△ABP三条边所在直线的斜率的乘积为t，求t的最大值；

分析：本题第（2）问的第①小问的难度系数是0.44，很少学生能成功做完.绝大多数学生设直线l的方程为y= k（x-1），与椭圆方程联立，在由消去y的过程中，大多数学生能得到（4k2+3）x2-8k2x+4k2-12=0，但也有部分同学化简出现错误.在正确得到学生在计算kPA·kPB=时，没有用y=k（x-1）及时消元，而是计算了y1+y2和y1·y2，由于复杂运算的步骤增加，出错率相当高，能正确得到kPA·kPB=-k-的少之又少.

三、在换元中求“简”

换元法在解题中经常被使用，是通过引进新的变量，把分散的条件联系起来，隐含的条件显露出来，或者把条件与结论联系起来，或者变为熟悉的形式，从而使复杂的计算和推证得到简化.

例5（第13题）已知函数f（x）=2x-1+a，g（x）=bf（1-x），其中a，b∈R，若满足不等式f（x）≥g（x）的解的最小值为2，则实数a的取值范围是_______.

分析：本题难度很大（难度系数为0.02），得分极低.求解中很多同学未能作好转化，若能注意换元法的应用，把复杂的指数问题转化为熟悉的二次函数零点分布问题，结合图像来处理，相信不少同学还是能够解决的.

解：由条件，不等式f（x）≥g（x），即2x-1+a≥b（2-x+a），令t=2x（t＞0），则不等式可化为t2+2（a-ab）t-2b≥0，问题转化为该不等式当t＞0时的解的最小值为4.设g（t）=t2+2（aab）t-2b，结合二次函数图像可得

当然，使用换元法时，需要遵循有利于运算、有利于标准化的原则，换元后要注重新变量范围的选取，一定要使新变量取值范围对应于原变量的取值范围，不能缩小也不能扩大.

四、在消元中求“简”

消元就是减少未知数的个数，把多元问题减元或转化成一元问题进行解决.消元的方法学生在初中就已经比较熟练了，但对消元思想，即使到高三，部分同学仍不具备，特别是在一些综合性较强的题目中，缺少将未知数个数由多化少，简化问题的意识.

分析：本题的难度系数为0.26，也就是说有75%的同学做错了，其中一大部分同学的错误答案是［3，12］，做法是对x1f（x2）利用x1和f（x2）各自的单调性去求，错在没有消元的意识.本题画出函数图像后（如图3），根据条件“若存在x1，x2∈R，当0≤x1＜4≤x2≤6时，f（x1）=f（x2）”，可得到x1∈［1，3］，x2∈［4，6］，其中x1∈［1，3］.这样就转化为一个常规的求三次函数在给定闭区间上的值域问题，此题目也就迎刃而解了.

图3

例7上文例4中的第（2）问的第②小问.

运算能力是学生解决问题的必备能力，要提高运算能力，我们先要关注运算细节.“细节决定成败”，运算的成败也在细节，“题海”让我们的学生习惯于耐心的去算，而忽略了运算中的规律探寻，没有了求简的意识.求简的过程是对运算细节的深度思考，也就是明道的过程.章建跃博士认为：“‘明道’，明即明白、懂得，道即规律、原则.明道者，明白原则、掌握规律也.老子说，‘人法地，地法天，天法道，道法自然’.因此，凡‘明道’者一定懂得按客观规律办事.”刘绍学教授提出：“数学是自然的，数学是清楚的.”其实这些都是要求我们广大教师要努力掌握数学的内在规律，并按这样的规律展开教学，对运算而言，就是要在求简中明道，在明道中求简.

1.陈志江.精耕细作低耗高效——和高三备课组长谈引领工作［J］.中学数学（上），2014（10）.

2.章建跃.数学教学的取势、明道、优术［J］.中小学数学（高中版），2013（4）.F