优化解题方法提升运算能力——谈圆锥曲线中椭圆问题的求解方法

☉浙江省奉化市第二中学　董　义

优化解题方法提升运算能力——谈圆锥曲线中椭圆问题的求解方法

☉浙江省奉化市第二中学董义

圆锥曲线中的椭圆问题始终是高考的热点之一.纵观近几年浙江省数学高考试题，椭圆问题年年考，且难度不小，试题呈现出综合性高、灵活多变等特点，尤其是其复杂的运算过程，使学生望而生畏.本文以几个高考题为例，谈谈此类问题求解的优化方法，化繁为简，提升运算能力.

一、回归定义，事半功倍

定义是揭示事物的本质属性，在数学解题过程中，回归定义并灵活运用，往往能获得事半功倍之效果.

分析：按常规思路，先求对称点Q的坐标，代入椭圆方程，整理得关于a、c的方程，其计算量巨大，短时间内无法完成.

优化方法：如图1，设F1（-c，0），连接QF1，易知OE为△FQF1的中位线，在Rt△FEO中，tan∠EOF=，求得于是|QF1|=由椭圆定义|QF|+|QF1|=2a，化简得b=c，得e=

图1

评注：通过创设另一个焦点，利用椭圆定义，建立一个关于a、b、c的方程，求得e，整个过程自然流畅，运算简洁.椭圆中涉及有关焦半径问题，应优先考虑用定义解题，简化运算.著名的李邦河院士曾说“数学是玩概念的”，概念是进行一切数学活动的基础，我们不仅仅只记住数学公式，更应重视对数学概念、定义的理解及应用，感悟数学本质.

二、妙用性质，峰回路转

椭圆的几何性质是解析几何重要内容之一，妙用几何性质，可以避免繁杂的代数运算，化繁为简，轻松解决问题.

例2（2011年浙江省数学高考理科第17题）设F1、F2分别为椭圆的焦点，点A、B在椭圆上，若则点A的坐标是______.

优化方法：如图2所示，延长直线AF1交椭圆于点B1，由椭圆的中心对称性知问题转化为了熟悉的直线与椭圆相交问题，可谓峰回路转，此题求解的方法甚多.

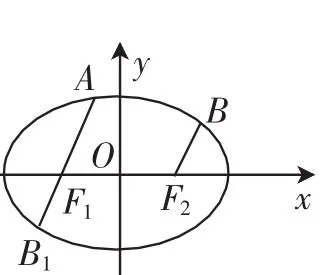
图2

又x1+5x2=-得x1=0，所以A（0，±1）.

评注：妙用椭圆的中心对称性质，通过数形结合，深刻直观地揭示了椭圆的本质属性，从而提高解题效率.

三、设而不求，出奇制胜

处理圆锥曲线中有关中点弦问题，“点差法”可谓是一种妙法.利用点差法，实现了舍而不求之目的，简化了解题过程，具有出奇制胜之效.

分析：省考试院给出的参考答案是利用直线AB与椭圆相交的位置关系，联立方程组，由韦达定理求得AB的中点坐标，代入直线方程，再结合Δ≥0，求解m的范围，计算烦琐，容易出错.

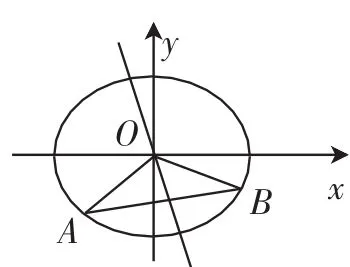
图3

优化方法：此题涉及中点弦，可用点差法求解，设AB的中点为M（x0，y0），A（x1，y1），B（x2，y2），由两式相减得），利用点M在椭圆内，，故实数m的取值范围为m>或

评注：“点差法”避免了解方程组带来的麻烦，降低了运算量，优化了解题过程.

四、伸缩变换，另辟蹊径

例4（2012年浙江省数学高考理科第21题）如图4，椭圆，其左焦点到点P（2，1）的距离为.不过原点O的直线l与椭圆C相交于A、B两点，且线段AB被直线OP平分.

图4

（1）求椭圆C的方程；

（2）求△ABP的面积取最大时直线l的方程.

分析：（1）略；（2）由点差法易求出直线AB的斜率，难度是△ABP面积的表示，虽然思路常规，但是运算量大，极易出错.学生普遍反映易入手，但拿高分困难.

图5

评注：椭圆中的三角形面积问题，若用常规方法求解运算量大，另辟蹊径，利用坐标的伸缩变换，把问题转为圆问题来解决，通过运用圆的性质，避开了解析几何烦琐的运算，化繁为简，甚是妙哉.这也正体现了数学中最基本的思想方法之一——转化思想.

椭圆问题的求解方法远不止这些，在解题教学过程中，我们应引导学生掌握其中的通性通法，感悟其中蕴含的数学思想方法，更应鼓励学生亲力亲为，克服心理障碍，扎实提升运算能力.

1.高娟，卜以军.圆锥曲线的三个重要结论及其应用［J］.高中数学教与学，2015（12）.

2.钟顺荣.利用伸缩变换求解直线与椭圆相切问题初探［J］.中学教研（数学），2015（3）.F