既要夯实“通性通法”，又要学会“灵活变通”——从两道高考试题的解法谈起

☉湖北省十堰市东风高级中学　张进华

既要夯实“通性通法”，又要学会“灵活变通”——从两道高考试题的解法谈起

☉湖北省十堰市东风高级中学张进华

每年的高考都会有让老师们津津乐道的佳作面世.每年的高考备考老师和学生都会有猜题、押题等应对的环节，各种模拟卷、参考书都极尽挖掘之能事，而对于考纲规定的有些内容则一笔带过，对于数学中的“通性通法”也没能很好地夯实.高考出卷者和各地老师也在玩躲猫猫，高考出卷者经常是“任凭风浪起，稳坐钓鱼台”，他们坚守自己的原则，从考纲和教材出发，从学生和实际出发，注重对数学内容全面考查，注重对数学的通性通法以及灵活运用数学能力的考查，我们先看一道题：

题1（2015湖北高考理科第14题）如图1，圆与轴相切于点T（1，0），与轴正半轴交于两点A，B（B在A的上方），且|AB|=2.

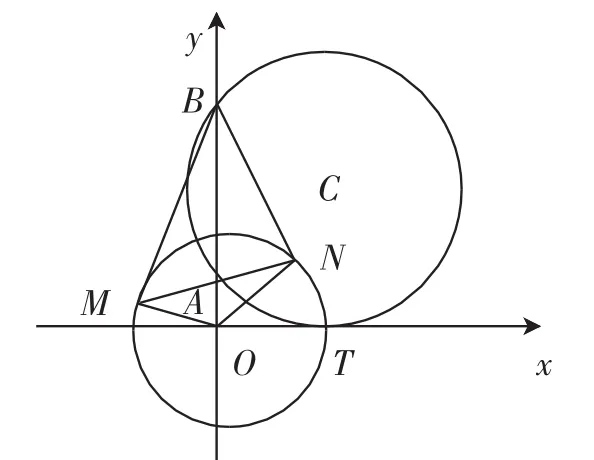
图1

（Ⅰ）圆C的标准方程为______.

（Ⅱ）过点A任作一条直线与圆O：x2+y2=1相交于M，N两点，下列三个结论：

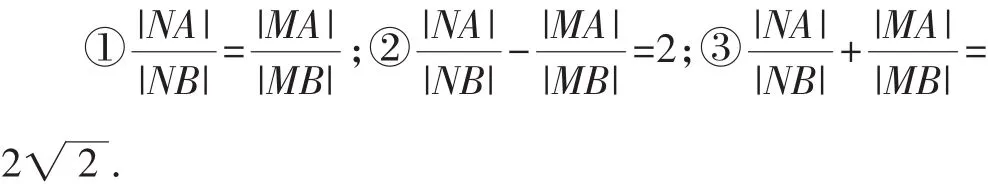
其中正确结论的序号是______（写出所有正确结论的序号）.

此题从面上看既像几何证明问题，又像解析几何问题，解决这道题存在一个方法选择的问题.

所以①②③均正确.

简评：本题是湖北高考填空题的第四题，若用三角形相似来解难度不大，并且三个命题可以同时判断，从高考反馈情况以及对现在学生的检测来看，这道题的得分情况非常差，并且耗费了较长的时间，出现这种情况的原因是对于选修4-1几何证明选讲的相关知识、尤其是对于我们不太常用的三角相形相似的判定定理没有牢固掌握.

设M（x1，y1），N（x2，y2），设x2>0那么kNB=

由（1）可得kx2=，将其代入（2）化简可得1.同理可得

所以①②③均正确.

简评：这种解法很严谨，但对于计算能力和应变能力要求太高，并且作为一个填空题花费的时间太长，学生没有耐心和信心坚持下去.

笔者关注了一些参考书上的参考答案，基本上都是用带入特殊值这种错误的方法，出现这种做法的原因是对于选修4-1几何证明选讲的相关知识没有牢固掌握，而对于解法2中的计算又不能熟练运用，所以手忙脚乱，连算带蒙，我们在高考备考中，还是要摒除侥幸，扎实应对，考纲规定的每一个章节，无论是必修，还是选修，我们都要夯实基础，夯实“通性通法”，同时还要做到灵活变通.

题2（2016届湖北八校高三第一次联考理科第20题）小明同学制作了一个简易的网球发射器，可用于帮忙练习定点接发球，如图2所示，网球场前半区、后半区总长为23.77米，球网的中间部分高度为0.914米，发射器固定安装在后半区离球网底部8米处中轴线上，发射方向与球网底部所在直线垂直.为计算方便，球场长度和球网中间高度分别按24米和1米计算，发射器和网球大小均忽略不计.如图3所示，以发射器所在位置为坐标原点建立平面直角坐标系xOy，x轴在地平面上的球场中轴线上，y轴垂直于地平面，单位长度为1米.已知若不考虑球网的影响，网球发射后的轨迹在方程k2）x2（k>0）表示的曲线上，其中k与发射方向有关.发射器的射程是指网球落地点的横坐标.

（Ⅰ）求发射器的最大射程；

（Ⅱ）请计算k在什么范围内，发射器能将球发过网（即网球飞行到球网正上空时，网球离地距离大于1米）？若发射器将网球发过球网后，在网球着地前，小明要想在前半区中轴线的正上空选择一个离地面2.55米处的击球点正好击中网球，试问击球点的横坐标a最大为多少？并请说明理由.

图2

图3

因此，最大射程为20米.

（Ⅱ）（法1）令y=2.55即（1+k2）x2-40kx+204=0.（1）

设（1）的两根为x1，x2且x1

要使击球点的横坐标a最大，

简评：这种解答自然、合理，大部分同学都利用这种解法，但很遗憾，很多学生在求x2的最值时没有办法进行下去，因为没有对x2进行分子有理化，损失惨重，分子有理化是我们在计算或者判断时常用的技巧，问题是我们对于这种技巧没有很好地夯实、归纳和总结，更谈不上娴熟地运用.

（法2）网球发过球网，满足x=8时y>1.

即a2k2-40ak+a2+204=0.

因为a≠0，故Δ=1600a2-4a2（a2+204）≥0，

简评：这种解法简洁、明了、省时、省力，只可惜很少有同学能跳出来用这种办法来解题，即把方程（1+k2）a2=2.55看成关于k的一元二次方程用Δ≥0求解，各种方法的“灵活变通”是我们高考复习中需要做好的“重点工程”，否则我们就不能“因地制宜”地去灵活应对.

题3（2015年广东高考理科第21题）数列｛an｝满足

（Ⅰ）求a3的值；

（Ⅱ）求数列｛an｝前n项和Tn；

（Ⅲ）令b1=a1，bn=

证明：数列｛bn｝的前n项和Sn满足Sn＜2+2lnn.

本题的关键是第三问中数列｛bn｝的前n项和Sn，笔者重点谈Sn求法.详细答案在此不再具体给出.

解：（Ⅰ）（Ⅱ）略.

当n≥2时，bn=（cn-cn-1）Tn-1+cn（Tn-Tn-1）=cnTn-cn-1Tn-1，故Sn=b1+b2+b3+…+bn=b1+（c2T2-c1T1）+（c3T3-c2T2）+…+

简评：这种解法很好，先构造一个数列，然后利用数列求和的常用办法——裂项相消可求出Sn，那怎么样才能想到构造一个数列呢？笔者认为来自于考生的感觉，只有有过硬的数学素养才能有感觉.

（法2）b1=a1=1，因为b2=

简评：该题是2015年广东高考题最后一题，我在班上让学生做了一下，结果让人大跌眼镜，学生用时20多分钟，居然没有一人能突破第三问（前两问很简单，学生用时不到5分钟），我所教的班可是省示范中学高三唯一的重点班.究其原因，学生都不能求出Sn，既不会用证法1构造数列后裂项相消，也不能用证法2通过观察归纳出Sn，它们均需要扎实的数学功底和高超的运用、应变能力.

高考考的是数学能力和数学素养，我们只有夯实了“通性通法”才能提高数学能力，我们只有学会了“灵活运用和变通”，才能提高数学素养，高考命题者有“任凭风浪起，稳坐钓鱼台”的修为和定力，我们高考备考者更要有“既夯实通性通法，又学会灵活变通”的勇气和决心，只有这样，我们才能在激烈的高考竞争中立于不败之地.Z