基于MPCK视角下的概念解读*——以凸多边形内角和为例
☉福建省厦门第一中学 王淼生
基于MPCK视角下的概念解读*——以凸多边形内角和为例
☉福建省厦门第一中学王淼生
一、MPCK理论
舒尔曼1986年提出PCK理论后,立即引起各国学者关注,从而使数学教师特有的学科教学知识从PCK泛学科的研究中独立出来,形成MPCK(数学教学内容知识)理论.MPCK理论要求教师不仅要有丰富、厚实的学科知识,更要有扎实、灵活的教学法知识,实现“冰冷、枯燥”的数学学术知识转化为“火热、生动”的教学(教育)知识,这是MPCK理论核心所在.概念教学历来是数学教学的重心与难点,尤其是跨越中小学多年段的数学概念更要引起高度重视.本文基于MPCK视角下的三角形内角和概念教学的点滴体会,敬请批评指正.
二、教材与解读
吃透教科书,领悟主编意图是MPCK理论视角下概念教学的具体体现.
文1在第38页“角的度量”一节中,通过射线给出了角的概念及直角、平角与周角等特殊角,同时介绍了测量角的工具——量角器.小学教科书主编这样精心设计的目的就是为了在文2第59页“三角形”一节中借助量角器来量出三角形三个内角的和等于180度(注:此时开始引入角度符号).同时把三角形三个内角剪下来拼在一起发现是一个平角.依据小学生的认知水平,以及年龄、心理特点,文1与文2侧重于小学生动手操作、直观感知等感性认识.考虑到小学生的实际情况,故而将理性认识(逻辑论证)留给后续教学(初中教学即文3与文4)来进一步处理.为了体现小学与初中的衔接,更是为了提醒一线教师有效实施小学与初中的过渡,初中教科书主编特意在文3第七章“三角形”的章引言指出:在小学我们通过测量得知三角形三个内角的和等于180度(形成与小学呼应).但三角形有无数多个,要说明任意一个三角形内角和都等于180度,不可能对所有三角形都进行测量,必须论证.章引言同时还指出三角形是最简单的平面图形,也是认识许多其他图形(凸多边形)的基础.借助三角形内角和等于180度,探究多边形内角和.不仅可以进一步认识三角形,而且还可以了解一些几何中研究问题的基本思想方法.鉴于初中生的认识水平、知识结构等,初中阶段应该逐步学会并顺利完成由说理到基本推理转变,即逻辑论证、度量计算,因为严谨是数学的生命所在.这正是初中教科书主编在文4中特意安排一章“几何的回顾”的原因.其中第一节“几何问题的处理方法”的目的就是为了说明有些几何命题可以通过观察、实验得到,但也有些命题仅仅通过实验、观察是不够的,还需要给予严谨的证明,让学生体会到逻辑论证的必要性与可行性.从小学到初中的过渡,教科书主编用心良苦,衔接十分到位又丝毫没有越位,全力作为而没有乱作为.文2在第67页通过实验发现“三角形三个内角的和等于180度”后,文2接着在第68页继续探究得到四边形内角和等于360度,意犹未尽,但又考虑到小学生的承受能力,怎么办?主编在第68页最下方提出一个问题:你能想办法求出六边形的内角和吗?为了彻底巩固,更为了与初中无缝对接,小学教科书主编在文2第69页的练习十六中特意设置了第4题:画一画,算一算,你发现了什么?原题如下:
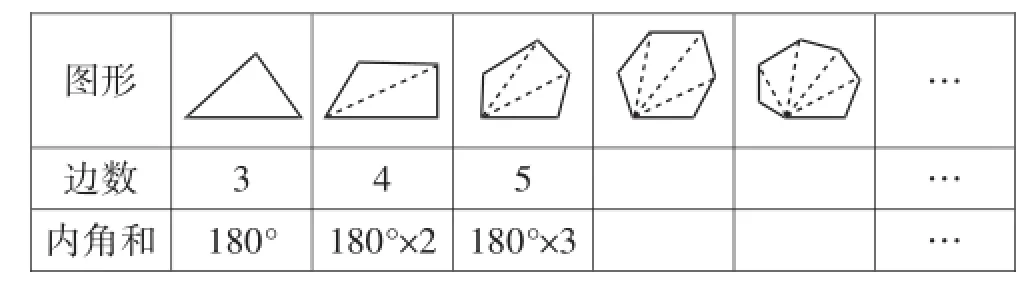
可以说小学教科书主编有意开始渗透类比思想方法,通过上述这个练习,将小学阶段的多边形内角和“作为”到恰到好处,正所谓“增之一分太长,减之一分太短.”正如波利亚所言:“类比是一个了不起的向导”,“类比是一个伟大的引路人”.紧接着初中教科书主编在小学基础上对多边形进行分割,文3第81~82页采取预留空白的形式进一步探究五边形、六边形、…、凸n边形内角和,限于初中生的知识水平,但又渗透类比与归纳等数学思想方法得出凸n边形内角和为(n-2)×180度.这就为高中深入研究并借助数学归纳法给予严谨证明留下伏笔.并在第82页右边的思考中提出“把一个多边形分成几个三角形,还有其他分法吗?”这样给师生又留下无限思考空间!作为呼应,初中教科书主编在文4第89页利用边空的形式再一次列出四边形、五边形、六边形、…、n边形的分法.至此,初中阶段就圆满完成既定的教学目标,高中将在初中基础上,针对凸n边形中的“n”属于n≥3,且n∈N,即有关正整数命题,这样与正整数相关的命题证明方法即高中数学归纳法呼之欲出,这正是主编在高中教科书即文6第二章“推理与证明”中安排第三节“数学归纳法”的原因所在.此外小学教科书主编在文2第61页指出“三角形具有稳定性”,这为高中立体几何即文7第42页展现公理2(过不在同一直线上的三点,有且只有一个平面)提供了实际案例.
上述通过对小学、初中及高中教科书的回顾与解读,不难看出从小学到初中再到高中可谓步步到位,承上启下,循环上升,无缝对接.
三、回顾与创新
MPCK理论不是一成不变,而是在特定概念教学中不断完善并创新.
1.三角形内角和
求任意凸多边形内角和,不仅对小学生,其实对于初中生来说也是较为困难,怎么办?我们可以先探究最简单的凸多边形,即三角形,正如著名的数学家华罗庚说:“要善于退,足够地退,退到最原始而不失去重要性的地方,是学好数学的诀窍.”那如何求三角形内角和呢?让我们顺着教科书主编的意图一起来回顾吧.
(1)小学测量观察法.
方法1:借助量角器直接测量三个内角的度数,并相加得到三个内角的和等于180度.
方法2:在纸上划出一个三角形,把三角形的三个内角剪下来,然后拼在一起,通过观察发现正好是一个平角,于是得到三角形内角和等于180度.
上述方法1与方法2正是小学生得到三角形内角和等于180度的思维方法与实施过程,其本质就是通过实验与观察,但数学是严谨的,对于数学结论必须给予严格证明,这为初中继续探究与论证指明了方向.
(2)初中初步论证法.
方法3:过点B作直线DE∥AC,则∠DBE为平角180度,如图1所示,利用平行线基本性质可得∠A=∠DBA(两条直线平行,内错角相等),∠C=∠CBE(两条直线平行,内错角相等)⇒∠A+∠B+∠C=∠DBA+∠ABC+∠CBE=180度.
方法4:在边AC上任取一点D(不含端点),则∠ADC为平角180度.过点D作DE∥AB,DF∥BC,分别交BC、AB于E、F,如图2所示,利用平行线基本性质可得∠A=∠EDC(两条直线平行,同位角相等),∠C=∠ADF(两条直线平行,同位角相等),∠B=∠EDF⇒∠A+∠B+∠C=∠EDC+∠EDF+∠ADF=180度.
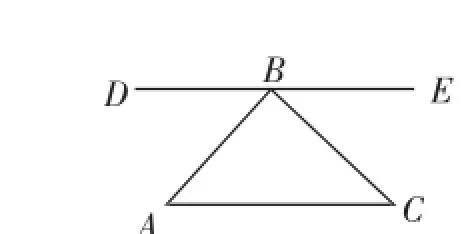
图1
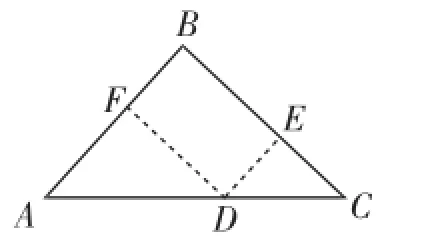
图2
方法5:延长AC至点D,则∠ACD为平角180度.过点C作CE∥AB,如图3所示,利用平行线基本性质可得∠ECD=∠A(两条直线平行,同位角相等),∠BCE=∠B(两条直线平行,内错角相等)⇒∠A+∠B+∠C=∠ECD+∠BCE+∠BCA=180度.
方法6:在三角形ABC内任取一点D(不含边界),过D分别作AB、BC、CA的平行线,分别相交于E、F;G、H;M、N,如图4所示,利用平行线基本性质可得∠A=∠EFG=∠EDN(两条直线平行,同位角相等),∠B=∠NED=∠FDG(两条直线平行,同位角相等),∠C=∠FGD=∠GDN(两条直线平行,同位角相等,内错角相等)⇒∠A+∠B+∠C=∠EDN+∠NDG+∠GDF=180度.
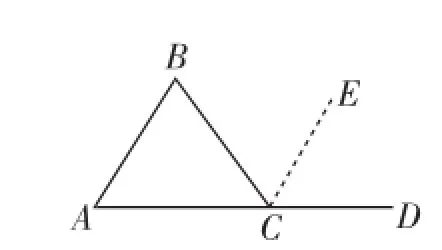
图3
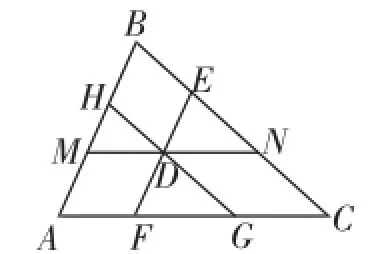
图4
2.三角形外角和
以上分析就事论事,都是从内角去考查,能否换一个角度呢?既然有内角,当然就会有对应的外角,那凸多边形的外角和为多少呢?我们依然退回到最原始、最基本的三角形,那三角形的外角和等于多少呢?
陈省身教授在北京大学的一次学术讲学中语惊四座:“人们常说,三角形内角和是180度,这是不对的!”大家愕然!怎么回事?三角形内角和等于180度,这不是数学常识吗?接着这位老教授对大家的疑问作了精辟解答:“说三角形内角和等于180度不对,不是说这个事实不对,而是说这种看问题的方式不对,应当说三角形的外角和等于360度.”“倘若把眼睛盯住内角,我们只能看到:三角形的内角和等于180度;四边形的内角和等于360度;五边形的内角和等于540度;…;n边形的内角和(n-2)×180度.这就找到了一个内角和公式.公式里出现了边数n.如果看外角呢?三角形的外角和等于360度;四边形的外角和等于360度;五边形的外角和等于360度;…;任意n边形的外角和等于360度.这就是把多种情形用一个十分简单的简论概括起来.用一个与n无关的常数代替了与n有关的公式,找到了更一般的规律.”
这个故事让我们想起了数学家波莱尔的一段话:“数学家的目的往往是寻求一般的解,他喜欢用几个一般的公式来解决许多特殊的问题.”因此,数学教学不是罗列更多的现象,也不是追求更妙的技巧,而是从更普遍的、更一般的角度寻求规律和答案.
方法7:三角形是一个静止的图形,我们从运动的观点,将静止转化为运动.让一个人沿着三角形周围走一圈,会发现这个人正好转了一圈,如图5所示,即三角形的外角和等于360度,而每一个平角都是180度,因此三角形的内角和等于3×180度-360度= 180度.
3.凸多边形内角和
上述方法7就是从运动与静止的相对关系来构造模型.同理可得,对于四边形也可以这样让一个人沿着四边形周围走一圈,会发现这个人也正好转了一圈,即四边形的外角和等于360度.事实上,让人沿着凸n边形周围走一圈,最后还是转了一圈回到原处,这就说明凸n边形的外角和是一个定值,恒为360度.
事实上,我们还可以由以下方法得到凸n边形的外角和恒为360度,如图6所示.
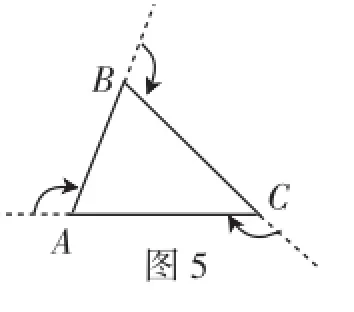
图5
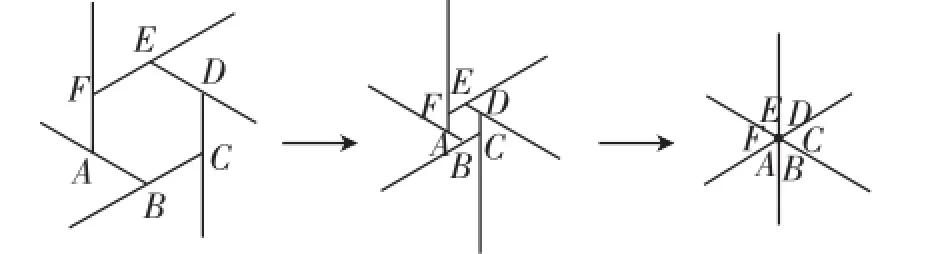
图6
有了这一新的发现,我们可以得到以下证法:
证法1:对于凸n边形,我们将凸n边形的每一条边都向同一个时针方向延长(射线),如图6中的第一个图,此时发现有n个平角,但是要减去所有的外角,故n边形的内角和等于n×180度-360度=(n-2)×180度.
对于上述得到的凸n边形的内角和等于(n-2)×180度,还可以有其他方法吗?我们观察(n-2)×180度相当于n-2个三角形的内角和,为此得到下面的证法:
证法2:对于凸n(n≥3,n∈N)边形A1A2A3…An,任取其中一个顶点,不妨取A1,将A1分别与A3、A4、…、An-1连接,这样的连线将凸n边形分割成n-2个三角形,如图7所示,故凸n边形的内角和为(n-2)×180度.
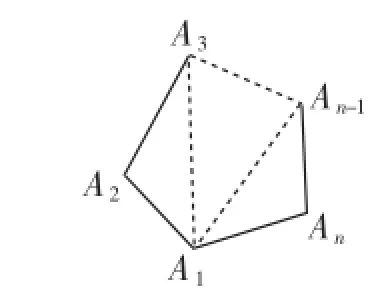
图7
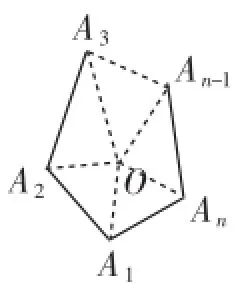
图8
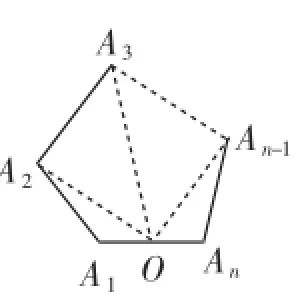
图9
倘若我们展开将得到(n-2)×180度=n×180度-360度①.此处n×180度表示什么呢?360度又意味着什么呢?n×180度表示n个三角形的内角和,360度表示一个周角,那么上述①式表示n个三角形的内角和减去一个周角.弄清它们的含义就可以得到以下精彩的解答.
证法3:对于凸n(n≥3,n∈N)边形A1A2A3…An,在其内部(不含边界)任取一点O,连接OA1、OA2、OA3、…、OAn,如图8所示,此时这样的连线将凸n边形分割成n个三角形,故其内角和为n×180度.同时应该减去顶角,即∠A1OA2+∠A2OA3+…+∠An-1OAn+∠AnOA1=360度.
故凸n边形的内角和为n×180度-360度.
让我们再一次审视上述凸n边形的内角和公式,并再一次适当变形为(n-2)×180度=(n-1)×180度-180度②
式②的右边表示什么意思呢?有什么含义呢?其实(n-1)×180度相当于n-1个三角形的内角和,减去180度就是减去一个平角,据此我们还可以得到以下证明.
证法4:对于凸n(n≥3,n∈N)边形A1A2A3…An,在其中一边(不妨在边A1An)上任取一点O(不含端点),连接OA2、OA3、…、OAn-1,如图9所示,此时这样的连线将凸n边形分割成n-1个三角形,即△A1OA2,△A2OA3,…,△An-1OAn故其内角和为(n-1)×180度,但同时应该减去一个平角即∠A1OAn,所以∠A1OA2+∠A2OA3+…+∠An-1OAn=180度.故凸n边形的内角和为(n-1)×180度-180度.
4.高中构思方法
上述都是从分割的角度来思考的,能否从有限与无限的辩证关系来寻求问题的解决呢?
证法5:三角形的内角和等于180度,四边形的内角和呢?五边形呢?凸n边形呢?对于四边形,我们只要连接其中一条对角线,此时四边形分成两个三角形,故四边形的内角和等于2×180度=360度③.
仿照上述方法可以将五边形分成三个三角形,此时五边形的内角和等于3×180度=540度④.
那凸n边形呢?上述③、④两式还可以这样来看:
对于四边形内角和:360度=2×180度=(4-2)×180度;
对于五边形内角和:540度=3×180度=(5-2)×180度;
由类比与归纳可得凸n边形内角和为(n-2)×180度.
上述分析是从特殊到一般的归纳方法,是一种不完全归纳法,当然不完全归纳法不一定正确,比如文5第101页~102页的“课题学习”材料中得到以下结论:三角形面积是它的中点三角形面积的4倍;四边形面积是它的中点四边形面积的2倍.然而对于五边形、六边形呢?事实上,五边形、六边形的面积与它的中点五边形、六边形的面积并没有固定的倍数关系,由此说明类比与归纳不一定正确,正如波利亚指出:“合情推理是危险的、有争议的和暂时的.”因此上述归纳得到的结论需要给予证明,这正是以后高中将要学习的数学归纳法.不妨设an=(n-2)×180度,以下用数学归纳法给予严格证明:
证法6:(1)当n=3时,显然成立;
(2)假设n=k(k≥3,k∈N)时命题成立,即ak=(k-2)× 180度,则当n=k+1时,我们将边A1Ak“撕裂”成两边,即边A1Ak+1与AkAk+1,这就相当于在原k边形基础上增加了一个三角形A1AkAk+1,如图10所示,即有ak+1=ak+180ak=(k-2)× 180+180=[(k+1)-2]×180度,故n=k+1时命题成立.
再由以上(1)、(2)可知,该命题对所有大于3的正整数均成立.
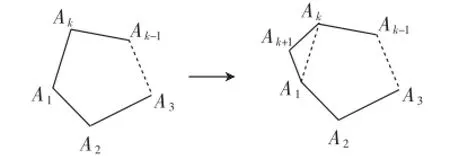
图10
数学归纳法是证明与正整数相关的命题的一种有效的方法,数学归纳法通过有限归纳无限,实现了从量变到质变的飞越,这正是数学归纳法的神奇与伟大.通过数学归纳法,让小学生、初中生克服了“无限”的瓶颈,只有跨越了“无限”,才能真正认识“无限”,实现从无限到有限的转化.其实数学归纳法既是一种演绎推理,又是一种归纳推理,因此,数学归纳法的实质是数学归纳——演绎法,将从小学到初中的学生一直憋在心中的疑团解开,而且为了将来在大学进一步学习第二数学归纳法、跳跃归纳法、倒退归纳法等留下伏笔,这正是交接而不脱节、到位而不越位的具体践行.
四、心得与感悟
仔细研读小学、初中、高中及大学教科书,深深敬佩这些主编们的精心设计与内容安排,像上述这样的案例还有很多,比如圆,小学在文8中通过对圆的认识学会作圆,以及求圆的周长和面积公式,接着初中在文4中从侧重于图形的角度研究了圆、直线与圆及圆与圆之间的位置关系,即定性研究,而高中则在文7中借助平面直角坐标系,即用代数坐标来表示几何点进行精确地定量研究,这样实现从数到形、从定性到定量,充分体现了解析几何的核心思想:用代数方法来定量研究几何问题,这就为大学继续深造空间解析几何打下了坚实的基础.
MPCK理论要求数学教师在审视概念时,要以全面、发展、系统的眼光.从小学、初中、高中乃至大学的数学教育是一个由感性到理性、由实践到理论、从具体到抽象、从特殊到一般、从说理到论证的过程,是一个循序渐进的螺旋上升的自然过程.有人说小学、初中、高中及高等数学就像一盘棋,数学教师就是这盘棋的对弈者,理应全盘考虑、全局考量、全权考究,才能下一盘精彩的对局,笔者更深切地感受到更像是4×100米接力赛,每一棒队员各就各位、各司其职.前一棒不仅要奋勇争先,还要为后一棒精心交接好,同时又要确保在规定的区域内完成交接棒.这就要求一线教师弄懂教材,吃透主编意图,掌握课标要求,清晰小学、初中、高中的教材从何处开始,在何处收尾,小学与初中的交接点在哪儿,初中与高中的衔接点又是什么,交接棒的区域是什么,只有这样才能真正做到概念教学交接而不脱节、到位而不越位,唯有这样才能演绎出数学概念教学魅力课堂.
1.课程教材研究所,小学数学课程教材研究开发中心.义务教育教科书(数学·四年级·上册)[M].北京:人民教育出版社,2014.
2.课程教材研究所,小学数学课程教材研究开发中心.义务教育教科书(数学·四年级·下册)[M].北京:人民教育出版社,2014.
3.课程教材研究所,中学数学课程教材研究开发中心.义务教育课程标准实验教科书(数学·七年级·下册)[M].北京:人民教育出版社,2010.
4.课程教材研究所,中学数学课程教材研究开发中心.义务教育课程标准实验教科书(数学·九年级·下册)[M].北京:人民教育出版社,2010.
5.王建磐.义务教育课程标准实验教科书(数学·初中三年级·下册)教师用书[M].上海:华东师范大学出版社,2008.
6.课程教材研究所,中学数学课程教材研究开发中心.普通高中课程标准实验教科书(数学·选修2-2)[M].北京:人民教育出版社,2015.
7.课程教材研究所,中学数学课程教材研究开发中心.普通高中课程标准实验教科书(数学·必修2)[M].北京:人民教育出版社,2008.
8.课程教材研究所,小学数学课程教材研究开发中心.义务教育教科书(数学·六年级·上册)[M].北京:人民教育出版社,2014.
9.孙凯.回到概念:基于对称,理解分类——以“圆的分类讨论问题”习题课为例[J].中学数学(下),2016(5).
*本文系全国教育科学“十二五”规划2015年度单位资助教育部规划课题《基于数学教学内容知识(MPCK)视角下的概念教学案例研究》(课题批准号:FHB150464)的研究成果.

