对一道与正方形有关的竞赛试题的变式探究

☉宁夏回族自治区中卫市沙坡头区宣和镇张洪学校　张　宁

对一道与正方形有关的竞赛试题的变式探究

☉宁夏回族自治区中卫市沙坡头区宣和镇张洪学校张宁

一、试题及解答

试题（2015年福建省初中数学竞赛试题）如图1，已知正方形ABCD的边长为1，点E、F分别在边BC、CD上，且∠EAF=45°，则△CEF的周长为_____.

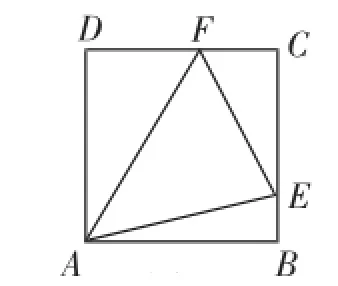
图1

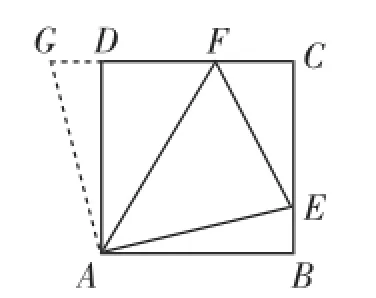
图2

解析：如图2，将△ABE绕点A沿逆时针方向旋转90°，得到△ADG，则△ABE≌△ADG，所以AE=AG，BE=DG，∠BAE=∠DAG.因为∠EAF=45°，所以∠GAF=∠GAD+∠DAF=∠BAE+∠DAF=90°-∠EAF=45°=∠EAF.在△EAF和△GAF中，AE=AG，∠EAF=∠GAF，AF=AF.所以△EAF≌△GAF，所以EF=GF.所以△CEF的周长为CE+CF+EF=1-BE+CF+GF=1-DG+CF+DG+DF=1+CF+ DF=1+1=2.

点评：本题主要考查正方形的性质、全等三角形的判定与性质、图形的旋转变换等知识，将△ABE绕点A沿逆时针方向旋转90°，构造△GAF，由此得出△EAF≌△GAF，从而证明EF=GF，这是解题的关键.通过证明可知，只要点F不与点D或点C重合，点E不与点B或点C重合，不论点E、F分别在边BC、CD上何处，只要保持∠EAF= 45°，即可得到△CEF，而且它的周长是一个定值，即△CEF的周长是正方形边长的两倍.本题中，点E、F是定角∠EAF=45°控制下的动点，△AEF与△CEF均是动态三角形，所以本题可以看作是动态几何中的定值问题.

二、变式探究

变式1：如图1，已知正方形ABCD的边长为1，点E、F分别在边BC、CD上，且△CEF的周长为2，求∠EAF的大小.

解析：如图2，将△ABE绕点A沿逆时针方向旋转90°，得到△ADG，则△ABE≌△ADG，所以AE=AG，BE=DG，∠BAE=∠DAG.由已知△CEF的周长为2，即CE+CF+EF= 2.因为CE=1-BE，CF=1-DF，所以1-BE+1-DF+EF=2，即EF=BE+DF=DG+DF=GF.在△EAF和△GAF中，AE=AG，EF=∠GF，AF=AF，所以△EAF≌△GAF，所以∠EAF=∠GAF.因为∠BAE=∠DAG，所以∠EAF=∠BAE+∠DAF.所以∠EAF+∠BAE+∠DAF=90°，所以∠EAF= 45°.

点评：由证明可知，只要点F不与点D或点C重合，点E不与点B或点C重合，不论点E、F分别在边BC、CD上何处，只要保持△CEF的周长是2，即△CEF的周长是正方形边长的两倍，则∠EAF=45°.显然，变式1是试题的逆命题.

变式2：如图1，已知正方形ABCD的边长为1，点E、F分别在边BC、CD上，当∠EAF=45°时，△AEF的面积是不是定值？如果不是，它有最大值还是最小值？请说明理由.

解析：由试题知，当∠EAF=45°时，EF=GF.如图2，令DF=x，BE=y，则FC=1-x，CE=1-y，DG=y.所以EF=GF=DF+ DG=x+y.

由试题或变式1知，S△AEF=S△AGF.

在Rt△CEF中，由勾股定理可知，FC2+CE2=EF2.

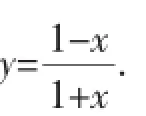
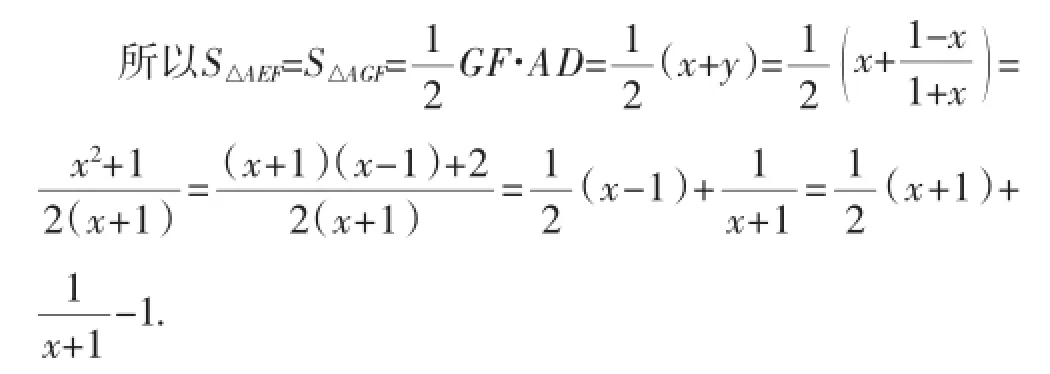
所以△AEF的面积不是定值.

变式3：如图1，已知正方形ABCD的边长为1，点E、F分别在边BC、CD上，当△CEF的周长是2时，△AEF的面积是不是定值？如果不是，它有最大值还是最小值？请说明理由.

解析：方法同变式2，请读者自行解答，此处从略.

在图1中连接BD，借助于几何画板或超级画板，笔者探究得到了变式4.

变式4：如图3，已知正方形ABCD的边长为1，点E、F分别在边BC、CD上，且∠EAF=45°，连接BD，BD分别交AF、AE于点M、N，求证：DM2+BN2=MN2.

证明：如图4，作点D关于直线AF的对称点G，连接MG、NG、AG，则△ADM≌△AGM，所以DM=GM，AD= AG，∠3=∠4，∠AMD=∠AMG.

因为四边形ABCD是正方形，所以AD=AB，∠1+∠2+∠3+∠4=90°.

因为AD=AG，∠2+∠3=45°，所以AB=AG，∠1+∠4= 45°.所以∠2+∠3=∠1+∠4，所以∠1=∠2.

又AN=AN，所以△AGN≌△ABN，所以BN=GN，∠ANB=∠ANG.

因为∠ADM=45°，所以∠AMD=180°-45°-∠4=135° -∠4.所以∠AMG=135°-∠4.

同理可知，∠ANG=135°-∠1.

所以∠MGN=360°-∠AMG-∠ANG-∠MAN=360°-（135°-∠4）-（135°-∠1）-45°=90°+（∠4+∠1）-45°=90°.

所以△MGN是直角三角形，所以GM2+GN2=MN2.

又因为DM=GM，BN=GN，所以DM2+BN2=MN2.

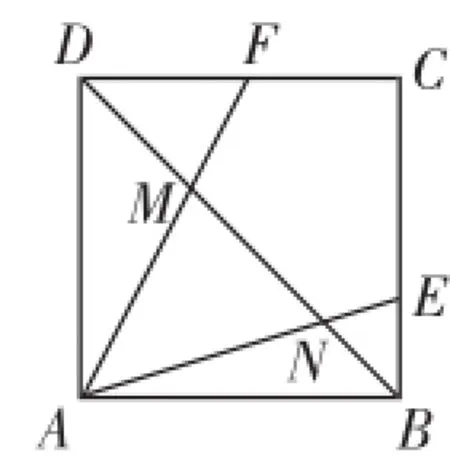
图3

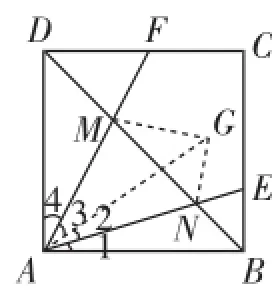
图4

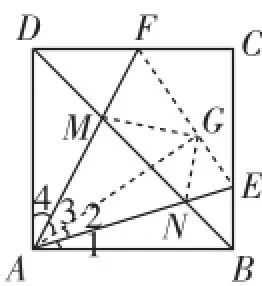
图5

点评：本题较为复杂，根据结论，易想到直角三角形中的勾股定理，因而需要将三条线段DM、BN、MN转化到一个三角形中，并证明这个三角形是直角三角形即可，图形变换是将分散的线段转化到同一个三角形的最基本工具，这也是解决这类问题的基本思路.由证明过程可知，∠AMG=135°-∠4，所以∠FMG=180°-（135°-∠4）=45°+∠4=45°+∠3，所以∠AGM=45°，所以AG平分∠MGN.

思考：在本题的证明过程中，点G是通过作点D关于直线AF的对称点而得到的，那么F、G、E这三点是不是在同一条直线上呢？

解析：如图5，连接FG、EG.因为点G和点D关于直线AF对称，所以△DFM≌△GFM，所以∠MDF=∠MGF= 45°.同理可知，∠NBE=∠NGE=45°.

所以∠FGE=∠MGF+∠MGN+∠NGE=45°+90°+45° =180°.

所以F、G、E这三点在同一条直线上.

说明：由以上证明易知，∠AGF=∠AGM+∠FGM= 45°+45°=90°，所以AG⊥EF.

在以上变式中，点M、N均在正方形ABCD的对角线BD上且不与点B、D重合，当点M、N中有一个点在对角线BD的延长线上时，线段DM、BN、MN之间存在什么样的关系呢？

经笔者探究，线段DM、BN、MN之间的关系依然是DM2+BN2=MN2.

变式5：如图6，已知正方形ABCD的边长为1，点E在边CD上且不与点D、C重合，点F在边CD的延长线上，且∠EAF=45°，AF交BD的延长线于点M，AE交BD于点N，求证：DM2+BN2=MN2.

证明：如图7，作点B关于直线AE的对称点G，连接MG、NG、AG、DG，则△ABN≌△AGN，所以BN=GN，AB= AG，∠1+∠2+∠3=∠4，∠AGN=∠ABN=45°.

因为四边形ABCD是正方形，所以AD=AB，∠3+∠4=90°.

因为AB=AG，∠2+∠3=∠EAF=45°，所以AD=AG，∠1=∠4-45°，∠2=45°-∠3=45°-（90°-∠4）=∠4-45°.所以∠1=∠2.

又AM=AM，所以△AGM≌△ADM，所以DM=GM，∠AGM=∠ADM=135°.

所以∠MGN=∠AGM-∠AGN=135°-45°=90°.

所以△MGN是直角三角形，所以GM2+GN2=MN2.

又因为DM=GM，BN=GN，所以DM2+BN2=MN2.

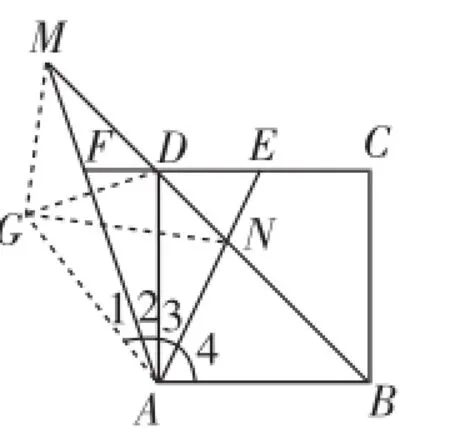
图7

点评：由此可知，当M、N中有一个点在对角线BD的延长线上时，线段DM、BN、MN之间的关系是DM2+BN2= MN2.本题与变式4相比，探究结论的思路与方法完全相同，但本题更具有挑战性.

三、关于几何试题变式的反思

对于几何试题的变式，其一，可考虑它的逆命题是否成立.其二，在保持基本图形不变的情况下，通过构造线段、角等基本图形，从而可得到一些新图形，然后借助于几何画板或超级画板等数学工具探索变化后图形中的角或线段之间的大小关系、线段之间位置关系等，最后通过人工推理，证明有关角或线段之间的大小关系、有关线段之间位置关系，从而得到几何试题的变式，这也是命制几何试题快速有效的方法之一.其三，可考虑对基本图形一般化，将等腰三角形、等边三角形、正方形、菱形、矩形、平行四边形等特殊图形一般化，或者将三角形变为四边形等.最后，验证原结论是否改变.如果结论不变，就要思考在新图形中如何证明结论；如果结论改变，会得到什么新结论，对新结论如何推理证明，这是进行几何试题变式探究的有效途径之一.对于变式而来的试题的使用，读者可根据命题的要求及考查目标，命制具有一定难度的试题.

1.张宁.从解法中寻求改进从变式中探究推广——对一道全国初中数学联合竞赛试题的变式与推广［J］.中学数学杂志，2016（4）.

2.张宁.追寻本质解法变式演绎精彩——一道竞赛题的解法及变式探究［J］.中学数学（下），2015（4）.

3.李玉荣.几道题的解法之我见［J］.中学数学（下），2016（4）.H