课件演示：化静为动，变虚为实——以“最短路径问题”为例

☉江苏苏州高新区第一中学　蔡映红

课件演示：化静为动，变虚为实——以“最短路径问题”为例

☉江苏苏州高新区第一中学蔡映红

科技的迅猛发展，给我们的教学工作带来了不小的变革.伴随着信息技术的发展，数学教育的价值、目标、内容及教学方式都产生了很大的变化.为了让数学教学与时俱进，在教学设计与实施过程中，我们应高度重视信息技术与教学内容的整合，“把现代信息技术作为学生学习数学和解决问题的有力工具”.近几年，一线教师将几何画板、GGB软件、flash软件、画图软件等教学软件引入到数学课堂上，将“静态遐想”化为“动态演示”，直观呈现几何图形的变化过程，为学生分析解题思路、验证数学猜想、形成解题过程等提供了极大的便利.基于这些数学教学软件所设计的教学活动，一般时间较短，呈现的是数学的核心知识的探究与应用过程，出现在课堂教学的关键时点上，是突破学生认知难点的“利器”.现结合一则基于几何画板之上的教学片断，谈谈课件演示的教学价值，希望能够引发您的思考.

一、“最短路径问题”教学片断

1.教学背景分析

“最短路径问题”是人教版八年级上学期第十三章“轴对称”中的一节内容，为本单元的“课题学习”.在学习这一内容前，学生已经学习了轴对称、轴对称图形、等腰三角形和等边三角形的知识，会画一些简单的轴对称图形.对“最短路径问题”的探索，让学生在前几节课上获得的知识与经验能够得到很好的应用，有利于这些知识的系统化和网络化.

2.教学片断简述

问题：如图1，牧马人从A地出发，到一条笔直的河边l饮马，然后到B地.牧马人到河边的什么地方饮马，可使所走的路径最短？

图1

投影“问题”，让学生读题，找出条件和结论，再独立思考，想想可以从哪些角度解决这一问题.学生思考片刻后，表示“没有找到方法”，但想到了前面学习的两个关于“最短”的定理：“两点之间线段最短”和“垂线段最短”，不知道是不是可以将这个问题转化到这两个知识上去？

此时，教师没有急于给出答案，而是打开课前用几何画板设计好的教学课件，如图2，在“河流”上设置动点D，并拖动动点使之在“河流”上自右向左滑动，请学生观察“计算”“BD+AD”的结果，并试着去找出使所走的路径最短的饮马点.

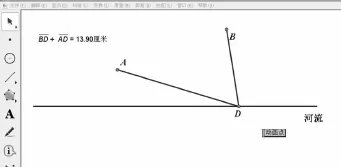
图2

第一次移动，学生未能发现符合要求的点的位置，但能明显感知到点D自右向左移动过程中，“BD+AD”经历了“由大变小，再变大”的过程，他们猜想“河流上应该存在一个饮马路径最短的点”.接下来，教师又进行了几次拖动演示，学生通过观察发现“BD+AD”的最小值为10.68厘米.于是，教师将点D定格在“BD+AD=10.68厘米”的位置上，如图3.

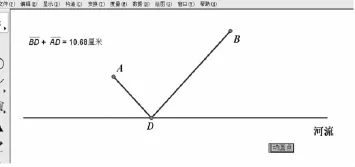
图3

接下来，在学生自主探究得出“作出图3中点D的方法”后，教师动画演示了作图过程，如图4.

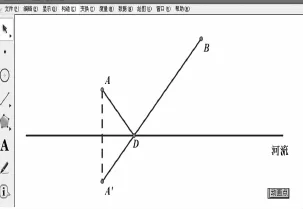
图4

最后，教师提出问题：为什么图4中的点D就是符合题意的“饮马点”呢？引导学生得出“再任意取一点，证明一下AD+BD最短”的说理思路.随后，教师继续利用课件演示，在“河流”上再取一点D′，连接AD′、BD′，如图5，请学生应用所学的知识去说明“BD+AD＜BD′+AD′”.

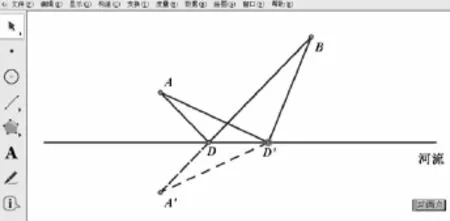
图5

二、片断分析

“最短路径问题”是初中几何的经典问题，饮马问题则是经典中的经典.本节课，是学生初次接触如此综合的极值问题，解题经验的不足给他们的思路探究带来了极大的困难.首先，线段之和最短问题的探究是第一次，学生无从下手；再去说明为何最短，更是难上加难.为了解决这一教学难点，教师借助几何画板软件，使点动起来，将数值“算”出来.在教师反复的拖动演示过程中，学生的目光只需锁定在变化的数值之上，形的问题在此刻就转化为了数的问题，发现符合题意的饮马位置自然就不是难事了.接下来的作图方法的探究，是学生基于软件演示之上的一种自主提升，有了前面的拖动变化和观察猜想，学生在发现点的位置后，自然会将与“最短路径问题”有较大关联的“轴对称的性质”和“两点之间，线段最短”联系起来.教师最后在图5中再取一点D′，对“为何最短”进行了说理，让学生明白了“要说明这里的最短，必须在这一个点之外再取一点进行比对”.“有对比才会有鉴别”，几何画板软件的教学应用，让原本固定不动的点动了起来，学生的思维由乏力的想象变成直观的感知，当他们将位置定格后，再回头探究画法、证明结论，新知探究的难度迅速下降！

三、教学价值分析

1.增加学生获取知识的途径

传统教学中，教师是课堂的“主角”，教师的讲授与学生的自悟是学生获取知识最主要的方式.《课标（2011版）》提出了“学生是学习的主体”的新理念，这让一线教师不得不改变自己的教学方式，努力设计出“能引发学生数学思考”的课堂活动.本文中呈现的课件演示，就是他们为此努力的成果.课件演示，图形变换由“静态”转化为“动态”，数学不再是“空想”，学生可以实实在在地经历观察、猜测、推理、验证等活动，教师期待的数学知识也会随着演示的进程和学生的探究自然出现.以课件为代表的信息技术的课堂融入，帮助学生突破了认知“困境”，为他们捕获“鲜活”的数学知识提供了极大的帮助.这些活动的出现，弥补了传统教学知识获得方式的“缺陷”，极大地丰富了学生获取知识的途径.

2.降低学生获取“四基”的难度

教师的教育理念决定了他的教学行为，不同理念下的课堂教学，会产生不同的学习行为.传统数学教学，受教学理念和教学条件的限制，学生的数学学习很大程度上定格在“思”上，这种“思”更多的是一种从教材出发的“空想”，很少有实践操作与互动交流.这种状况下，数学知识的获得、数学技能的形成、数学思想的感悟和数学活动经验的积累都是较为困难的.《课标（2011版）》提出了让学生获取“四基”的总目标，数学的基本思想和基本活动经验是新增的“双基”，它们是隐形的，是在学生经过完整的探究过程后才能体验与感悟的.这就要求一线教师必须转变教育理念，改变自己的教学方式，让学生的五官和大脑在课上同步“动起来”，多渠道获取有用的信息，从而降低学生获取“四基”的难度.上面的课堂活动中，学生不仅可以动手做，还能仔细看，活动过程中的及时抽象，让他们不得不认真地想.这样的教学，很好地弥补了传统教学方式“过于抽象”的不足，数学知识的出现更为直观、具体、便捷，让每一名学生都有机会和可能参与到知识的发现与生成过程之中，他们在时间和空间许可的范围内主动积极地展开探究，不断获取数学的基础知识、基本技能、基本思想和基本活动经验.

3.强化学生对数学本质的认识

“数学是研究数量关系和空间形式的科学”，“数量关系和空间形式”是数学的本质所在.然而，在初中阶段，一些外在的情境常会“遮掩”住数学的本质，使学生无法透过现象正视数学本质.为此，这一阶段的数学学习应“遵循着实践、认识、再实践、再认识……的认识规律”，让学生在反反复复的琢磨后逐步接近数学的本质，加深对“数量关系和空间形式”的认识.课件演示正是在这样的教学需求下形成的，这些活动的出现打破了教师唱独角戏的传统教学形式，为课堂教学注入了新的活力.演示，师生的操作与交流指向了思路的分析，“变与不变”的直观感知是一种体验，更是一种感悟，隐藏其中的“四基”也就是在这种体验与感悟中自然生成的.很明显，课件的直观演示成为了化解学生认知难点的辅助工具，学生在获取数学知识的同时，对数学本质的认识也就会越来越深了.

4.培养学生学习数学的兴趣

人的任何认知活动都离不开兴趣，在学生进行数学学习时，兴趣是他们最好的老师.为此，教师应设计出符合学生认知规律的课堂活动，不断培养学生学习数学的兴趣.“嵌入式”课堂活动，教学形式多样，教学手段先进，出现时机适宜，完全能担起培养学生学习兴趣的重任.在学生认知的“拐点”处，课件的及时出现，与其他课堂活动的精准“对接”，让教师教与学生学的方式迅速改变.新的教学方式的出现，让原本平静的课堂泛起一丝“涟漪”.新的教学手段与教学行为的出现，极大地刺激学生的感官，学生的学习兴趣瞬间激发，学习的积极性被调动起来，活动的成效自不必说了.这种不同形式的教学活动的交替呈现，在每一节课上都能让学生的思维形成兴奋点，学习数学的兴趣在此过程中也就自然地得到了强化，为他们的数学学习注入不竭的动力.

5.提升了学生的综合素养

数学是一门基础性学科，它不仅服务于学生的学习，还影响着学生的生活.“义务教育的数学课程能为学生的未来的生活、工作和学习奠定重要的基础”，我们不仅要让学生获得必备的基础知识和基本技能，还应让他们学会数学地思考，用数学的眼光看世界.传统教学非常重视学生数学知识获取和应用能力的培养，这一点是值得称道的，我们应将这一做法一以贯之地坚持下去.课件演示作为传统教学的补充，它在关注知识教学的同时，还十分重视学生综合素养的提升.课件演示的过程全方位调动了学生，不仅学生的五官会参与到学习中来，学生的大脑更是不停地运转，积极地将学科内外的经验和知识调取出来，会参与到知识的获取与应用的过程之中.他们收获的可能不仅仅是数学的知识，还有问题解决的经验，当然，伴随着这些数学知识与经验的获得，还会出现一些新的超越学科界限的知识与经验，它们也会迅速地融入到学生的认知结构之中，转化成个体“内敛”的素养.

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2.林夏水.数学本质·认识论·数学观——简评“对数学本质的认识”［J］.数学教育学报，2002（11）.

3.蒲大勇.例析数学模型的建构与演绎［J］.中学数学杂志（初中版），2014（6）.

4.邢成云.经验打底画板助力——八年级《13.4课题学习最短路径问题》教学设计［J］.中学数学（下），2014（4）.Z