数形结合：让理解走向深刻——“有多大”的教学启示

☉江苏省盐城市第五初级中学　华云锋

☉江苏省盐城市第五初级中学华云锋

估算能力是运算能力的重要组成部分，较强的估算能力有利于学生发现并形成便捷的运算途径.为了培养学生的估算能力，在“实数”单元中，笔者设计了一次探究活动“有多大呢”，意在让学生从的大小探究入手，形成估计无理数（尤其是开方开不尽的无理数）大小的能力.由于学生刚刚接触算术平方根，对一个正数的算术平方根的大小没有直观的感知，因此，想要从数的角度直接发展其估算能力绝非易事.为此，在组织这一探究活动时，笔者以形引数，数形结合，将繁杂的计算与正方形的面积、边长结合在一起，使学生对估算取值的必要性和有效性有了较为清晰的认知，推动其对估算的理解走向深刻.现呈现这一教学片断，并谈一些个人的体会，说得不对的，敬请批评指正.

一、教学背景分析

本节课是在学生学习了算术平方根的定义、表示方法、计算方法后对算术平方根的继续学习.虽然在学习算术平方根过程中，学生已经积累了一定的经验，但一个新的“数种”的进入，想要在一节课上就达到知识与经验的网络化是不大可能的.因此，本节课的教学既是对新知的探究，也是对旧知的巩固.课上，探究“有多大”之前，笔者已经安排了“探究：能否用两个面积为1dm2的小正方形拼成一个面积为2dm2的大正方形”，这个活动是上一节课认知的自然延续，也是本节课新知探究的开端，用好这个“探究”，将有利于学生体会到估算的必要性和有效性.

二、教学片断及分析

1.拼图探究，观察边的长短

探究：能否用两个面积为1dm2的小正方形拼成一个面积为2dm2的大正方形？

学生拿出桌上的两个边长为1dm的小正方形（说明：教师课前已经将探究需要用到的正方形纸片发给了学生），在小组中展开探究.教师取出一个边长为1dm的正方形纸片贴在黑板上，并写上边长1dm，如图1.

图1

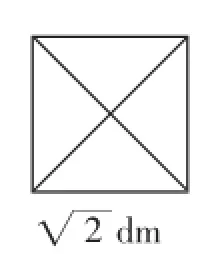
图2

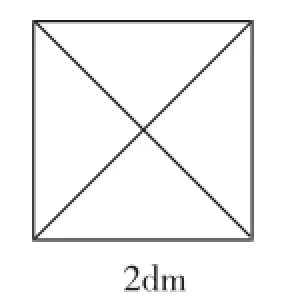
图3

3分钟后，不少小组探究得出方法.教师让一个小组将拼图方法进行了交流，并将其拼得的图形贴在黑板上，然后在图的下方写上”，如图2.接下来，教师继续追问：你能利用面积为2dm2的两个正方形拼成一个面积为4dm2的大正方形吗？

学生很快给出图3，教师顺势在其下方将其边长“2dm”板书，然后指着三幅图，提问：从左往右，这三个正方形的面积发生了怎样的变化？学生齐答：变大！教师又问：边长又是怎么变的呢？学生再答：变长！教师继续追问：你能总结出正方形面积变化与边长变化的规律吗？在一番交流后，得出结论：正方形的面积的变化，会带来其边长的变化，面积变大，边长也会变长.

评析：裁剪正方形，再进行拼图，学生是有这方面的经验的.以这样一则探究引入，教者顺应了教材的编排，从学生的已有“认知水平”展开“可能的教学”.图1至图3的逐步呈现，为的是让学生明晰“正方形的面积与边长之间有着对应的大小关系”，这是学生探究“有多大”的知识基础和经验基础.教者基于图形的一问一答，让学生脑海中与正方形相关的形的知识得以回顾，同时对边长的标注，又让形与数产生了联系，这对下面的探究是十分重要的.

2.数形结合，感知数的大小

教师指着图1和图3说：这两幅图中，正方形的边长为1dm和2dm，边长都是整数.请你也用一个整数来表示图2中的边长！

原本热闹的教室立即安静下来，很多学生陷入沉思.

教师再度发问：这样的整数有吗？

学生齐答：没有！

教师立即追问：为什么？

一名学生给出了十分准确的理由：根据刚才的拼图，我发现面积越大，边长越长；边长越长，面积也就越大，正方形的边长的大小与其面积有直接的关系.所以，边长为dm的正方形的面积为2dm2，而边长为1dm的正方形的面积为1dm2，边长为2dm的正方形的面积为4dm2.三个面积（单位：dm2）由小到大排序为1＜2＜4，所以其边长（单位：dm）的对应排序为1＜＜2，在1和2之间是不存在整数的.因此，没有这样的整数边长，使其面积为2dm2.

教师笑问：那就不是整数喽？

再从东晋臣民的官方学校教育来看，其官学教育也主要是儒学教育，这与南朝官学的儒、玄、文、史四科的分设与对立有很大的不同。

学生再次齐答：不是整数！

学生纷纷给出自己的猜想，有说1.1的，有说1.2的，也有说1.3、1.5的.

学生说：从面积的角度，也就是算出边长为1.2、1.3、1.4、1.5、…的正方形的面积，谁最接近2，谁的边长就最接近.

教师让学生自己去算一算这些边长下的面积，很快有学生说出，应比1.4大，比1.5小.其理由为1.42= 1.96，1.52=2.25，因为1.96＜2＜2.25，所以1.4＜＜1.5.

接下来，教师追问，边长为1.4几的正方形面积与2更接近呢？学生分组探究，每人从1.41～1.49中分别挑选出两个数，并计算它们的平方，进而交流得出“1.41＜＜1.42”……

3.拓展应用，探究经验再用

评析：通过上面两个活动的探究，学生已经积累下了估算的经验.在经验和知识向能力转化的过程中，适量的练习是不可缺失的.教者这里安排的探究“有多大”，难度不大，问题解决的过程仅实现了刚刚获得知识、经验的简单应用，当然，在这样的简单重复中，不少同学会自觉地将其与已有的知识比如“结果精确到0.01”等产生联系，使之转变为知识网络的一部分.

三、三点感悟

1.估算能力培养应向四基借力

估算能力的培养是《义务教育数学课程标准（2011年版）》（下称《课标（2011年版）》）提出的“新要求”.对估算能力的培养离不开四基教学，我们应将其融入到常态教学之中，以数学的基础知识、基本技能、基本思想和基本活动经验教学为抓手，不断提升学生的估算能力.以本节课为例，探究“有多大”是课堂教学的一个小的环节，除了这个探究活动，全课还有拼图探究和用计算器求值及规律探究等活动，如此大的课堂容量，对“有多大”的探究显然不能成为核心活动.因此，在我们的教学中，把握好估算能力培养的“度”，就显得十分重要了.在这节课上，我们仅能将这一探究作为学生获得四基的一个中间环节，将其“嵌入”到算术平方根的计算及性质认知历程之中，花个五、六分钟就可以了.

2.实数教学依托数形结合给力

实数是学生进入初中后数域拓展的结果，由于没有太多的知识与经验作为认知的基础，学生获得这一知识是较为困难的.为此，我们经充分调用学生已有的知识和经验，将数与形结合起来，让学生在形的辨析中感知实数及其相关概念的内涵，进而体会到实数，尤其是无理数的大小.正是基于这样的考虑，在引入算术平方根和探究“有多大”之前都安排了一个与正方形有关的实际问题，在接下来学习立方根和探究立方根的性质前，同样安排了一个与正方体有关的实际问题，两个与实数相关的概念的引入都是从形开始的，所以，我们在教学中应重视形向数的转化，更要将数与形联系起来，在数形结合与形数转化中揭示实数相关的概念及其性质.

3.经验固化需要反复实践发力

数学基本活动经验是《课标（2011年版）》提出的“四基”之一，它是学生获取数学知识、形成基本技能的重要源泉.在初中阶段的教学中，类比认知是较为常见的获取新知的途径，因此，我们要高度重视数学基本活动经验的延续和应用.这种经验的延续和应用，应该建立在学生已有经验之上的自然生长，必要的反复实践将有利于新生经验的固化，使之与学生的固有经验融合，嵌入到已有的知识网络中去.以本文案例中的估算为例，学生获取估算方法“逼近法”的过程积累下很多探究与应用的经验，这些经验在接下来的学习中将会通过不定期的实践反复巩固，每一次对新数据的估算都将是对这次探究所“诞生”经验的回顾与矫正，必将会推动这些与估算能力养成息息相关的经验的网络化建构.

1.印冬建.培养运算能力推动“四基”教学——以人教版教材七年级上册教学为例［J］.中国数学教育（初中版），2014（11）.

2.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

3.林群.义务教育教科书·数学（七年级下册）［M］.北京：人民教育出版社，2012.

4.林群.义务教育教科书教师教学用书·数学（七年级下册）［M］.北京：人民教育出版社，2012.

5.马君琴.立足思维习惯训练强化运算能力培养——以“1.4.2有理数的除法（2）”为例［J］.中学数学（下），2014（12）.H