解析法“以不变应万变”突破中考动态难题

☉浙江省衢州市实验学校　邓　达

☉浙江省衢州市衢江区杜泽中学余小飞

解析法“以不变应万变”突破中考动态难题

☉浙江省衢州市实验学校邓达

☉浙江省衢州市衢江区杜泽中学余小飞

《义务教育数学课程标准（2011年版）》提出用坐标研究图形的性质、探索坐标变化与图形运动变换之间的变化规律和对应关系.［1］将图形放置于平面直角坐标系中，用坐标的方法研究图形，更好地揭示了数学是研究数量关系和空间形式的科学的思想内涵.［2］动态问题囊括了对学生的数感、符号意识、空间观念、几何直观、运算能力、推理能力、模型思想、应用意识、创新意识的考查，是当下全国各地初中学业水平考试命题者最爱考查的对象之一.它往往通过点的运动、线的移动导致整个图形跟着发生变化，而初中生的空间想象能力和几何直观感受力并不强，以至于命题者能通过几何画板直观看出图形运动变化的全过程很难在学生脑海中呈现.因此，很多学生对于此类问题都有“恐惧感”.解析法通过数形结合在平面直角坐标系中，把几何动态问题转化为代数问题，很好地帮助学生突破动态这一难点.本文着重介绍用解析法突破以下几类动态问题.

一、等腰三角形

例1如图1，在矩形ABCD中，AB=4，BC=8，动点P以每秒1个单位长度的速度从点D出发向终点A运动，同时动点Q以每秒个单位长度的速度从点A出发沿对角线AC向终点C运动.过点P作PE∥DC，交AC于点E.设动点P、Q的运动时间为x秒，当点P运动到点A时，P、Q两点同时停止运动.

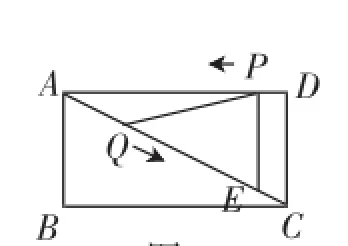
图1

（1）设PE=y，求y关于x的函数表达式.

（2）在点P、Q的运动过程中，是否存在这样的P和Q，使以P、Q、E为顶点的三角形是等腰三角形？若存在，请求出所有满足要求的x的值；若不存在，请说明理由.

分析：第（1）小问比较简单，就不赘述了.对于第（2）小问，题目通过动点P从点D出发向终点A运动，引起线段PE的长度和位置都发生变化，点Q从点A出发沿对角线AC向终点C运动，使得△PQE在整个运动过程中，形状和位置都在发生变化，学生对于是否存在这样的P和Q，使以P、Q、E为顶点的三角形是等腰三角形感到比较棘手.这一问到底有几个答案呢？学生心里也没底.由题意，通过画动态定位分类图讨论，［3］经历动态过程，［4］可以知道，要先根据点Q与点E的位置分为相遇前、相遇后两类，然后分别讨论PQ=PE、PQ=EQ、PE=EQ这三种情况.在此讨论的基础上，分别画出相应的图形，根据等腰三角形及三角形相似的性质，建立方程，并求解.在此过程中，由于点、线的移动，导致△PQE在不断变化，大部分学生很难把整个运动过程分析清楚，并画出满足条件的图形，进而较难得到全部答案.基于此，可以考虑建立平面直角坐标系，如图2，以B为坐标原点，以BC所在直线为x轴，AB所在直线为y轴，把P、Q、E三点的坐标用含x的代数式表示出来，然后用两点间的距离公式分别表示PQ、EQ、PE，再根据PQ=PE、PQ=EQ、PE=EQ这三种情况得到三个方程，解一元二次方程即可.

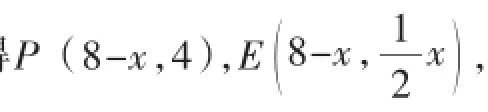
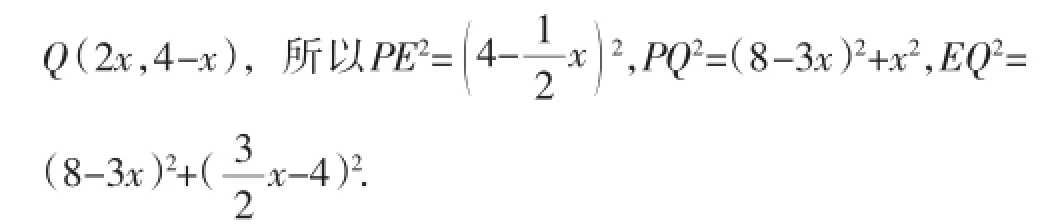
图2

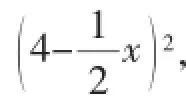
反思：△PQE在运动过程中时刻都在发生变化，给学生对图形运动的分析带来一定的障碍.运用解析法，学生只需把P、Q、E三点的坐标用含x的代数式表示出来，通过两点间的距离公式建立方程，把几何问题代数化，大大减少了对图形运动过程的分析.菱形的存在性问题也可以根据菱形的性质与判定转化为平行四边形、等腰三角形的存在性问题，再仿照上述过程就能解决.

二、平行四边形

例2（2014年山西卷）综合与探究：如图3，在平面直角坐标系xOy中，四边形OABC是平行四边形，A、C两点的坐标分别为（4，0）、（-2，3），抛物线W经过O、A、C三点，D是抛物线W的顶点.

（1）求抛物线W的解析式及顶点D的坐标.

（2）将抛物线W和▱OABC一起先向右平移4个单位后，再向下平移m（0＜m＜3）个单位，得到抛物线W′和▱O′A′B′C′，在向下平移的过程中，设▱O′A′B′C′与▱OABC的重叠部分的面积为S，试探究：当m为何值时，S有最大值？并求出S的最大值.

（3）在（2）的条件下，当S取最大值时，设此时抛物线W′的顶点为F，若点M是x轴上的动点，点N是抛物线W′上的动点，试判断是否存在这样的点M和点N，使得以D、F、M、N为顶点的四边形是平行四边形？若存在，请直接写出点M的坐标；若不存在，请说明理由.

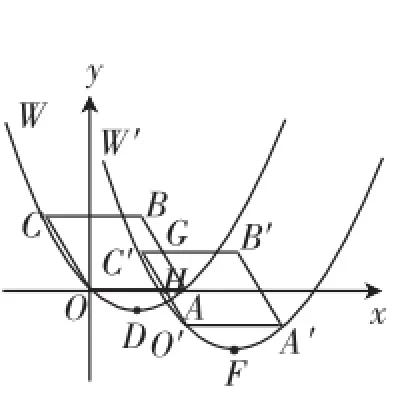
图3

分析：第（1）、（2）两问不作讨论.本题的图形在将抛物线W和▱OABC一起经过两次平移后变得很复杂.而在复杂图形中提炼出与解决问题相关的部分图形，是学生很难做到的.第（3）小问的常规思路是根据平行四边形的判定“一组对边平行且相等的四边形是平行四边形”和“对角线互相平分的四边形是平行四边形”去寻找满足条件的点，找到大致位置后通过构造全等三角形来求出点的坐标.在复杂图形的背景下，第（3）问中平行四边形的双动点存在性问题，学生很难找全所有的答案.用解析法只需要设M（x，0），然后把点N的坐标用含x的代数式表示出来，然后代入抛物线W′的表达式，解方程即可求出所有的解.

（3）设M（x，0），如图4，从图3中提炼出△DFM，然后分别过点D、F、M作对边的平行线，交于点N1、N2、N3.

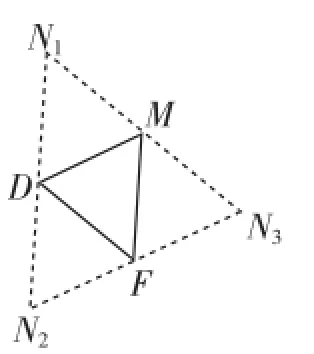
图4

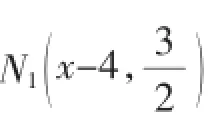
综上所述，存在这样的点M和点N，点M的坐标分别为（0，0），（4，0），（6，0），（14，0）.

反思：通过两次平移，题目的图形变得很复杂，对学生的审题造成干扰.在此基础上，设置M是x轴上的动点，N是抛物线W′上的动点，给学生对图形的动态分析造成很大的障碍.解决动态问题最好的办法就是化动为静，［5］第（3）问中有两个动点，当设M（x，0）时，把点M看成静点，而平行四边形已知三个点时，第四个点就只有三种情况了，基于这个想法，只需提炼出图4，就能做到“化动为静”、“化繁为简”.

三、矩形

例3（2015年成都卷）如图5，在平面直角坐标系xOy中，抛物线y=ax2-2ax-3a（a＜0）与x轴交于A、B两点（点A在点B的左侧），经过点A的直线l：y= kx+b与y轴交于点C，与抛物线的另一个交点为D，且CD=4AC.

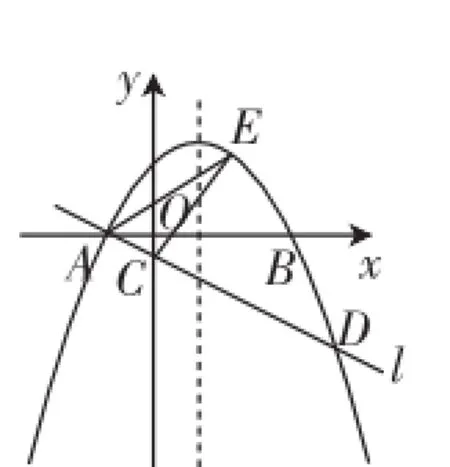
图5

（1）直接写出点A的坐标，并求直线l的函数表达式（其中k、b用含a的式子表示）.

（2）点E是直线l上方的抛物线上的一点，若△ACE的面积的最大值为求a的值.

（3）设P是抛物线对称轴上的一点，点Q在抛物线上，以A、D、P、Q为顶点的四边形能否成为矩形？若能，求出点P的坐标；若不能，请说明理由.

分析：本题抛物线的表达式待定，直线l的表达式由a的值确定，点D是直线l与抛物线的交点，依题意，只能得到点D的横坐标为4，点D的纵坐标为5a，同时P是抛物线的对称轴上的动点，Q是抛物线上的动点.太多不确定的量，让绝大多数学生望而却步！解析法可以减少对动态图形的分析.根据矩形的定义“有一个角是直角的平行四边形叫做矩形”，第（3）小问可以转化为两个问题来解决：①平行四边形的存在性问题，解决的方法与例2完全类似；②直角三角形的判定，解决方法可用勾股定理的逆定理.

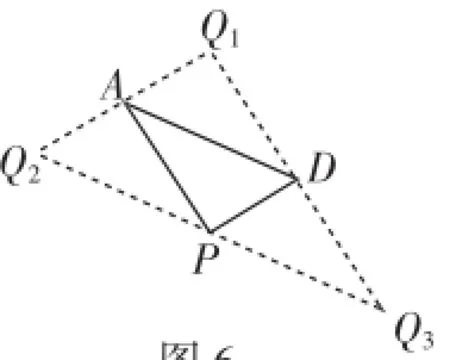
图6

解：（1）点A（-1，0），直线l的函数表达式为y=ax+a.

（3）设点P（1，m），由题意可知，点A（-1，0），D（4，5a），a＜0，如图6（从图5中提炼），与例2的方法类似.

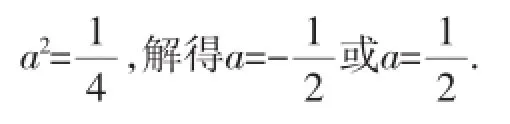
因为a＜0，所以m=-4，所以P（1，-4）.

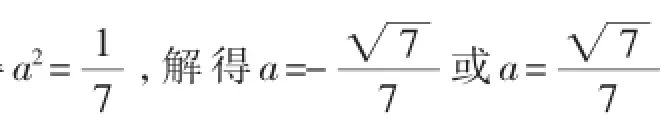
③当DP为对角线时，可得Q3（6，5a+m），由Q是抛物线上的点，可得Q3（6，21a），则5a+m=21a，m=16a.由DP2= AD2+AP2，得到方程32+（m-5a）2=52+（5a）2+22+m2，整理可得16a2=-2，此方程无实数解.

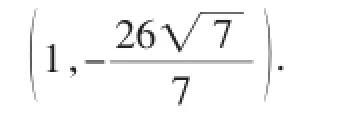
反思：本题中的抛物线和直线的表达式都是含参数的，再设置动点P、Q，动态的量太多，让学生不知道应该怎么去画图分析.通过把矩形存在性问题分解成两个问题，借助于平行四边形和直角三角形的判定，用解析法就能很方便地解决问题.另外，直角三角形的存在性问题可由勾股定理的逆定理建立方程解决，也可用k1·k2= -1来建立方程解决（这种方法已超纲，但可以给学有余力的同学补充）.

四、正方形

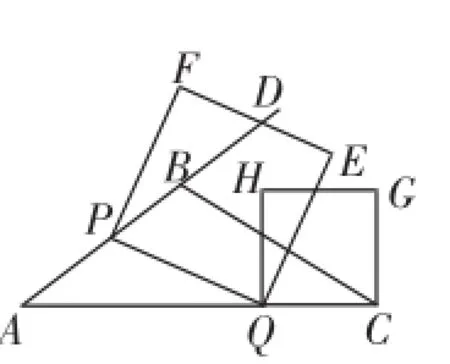
图7

（1）求tanA的值.

（2）设点P运动时间为t，正方形PQEF的面积为S，请探究S是否存在最小值.若存在，求出这个最小值；若不存在，请说明理由.

（3）当t为何值时，正方形PQEF的某个顶点（Q点除外）落在正方形QCGH的边上？请直接写出t的值.

分析：第（1）、（2）问不再赘述了.对于第（3）问，由点P、Q的运动，引起线段CQ的长度，以及PQ的位置和长度不断发生变化，进一步导致正方形QCGH与正方形PQEF的形状与大小也发生变化.在此基础上设问：“正方形PQEF的某个顶点（Q点除外）落在正方形QCGH的边上”，大部分学生直接放弃，对“一个正方形的顶点落在另一个正方形的边上”的内涵是什么不理解，尤其是当点P、Q在运动时，作不出相应符合要求的位置图形，失去了图形的直观性之后丧失了继续探究的信心.用解析法可以减少对图形运动过程的分析.

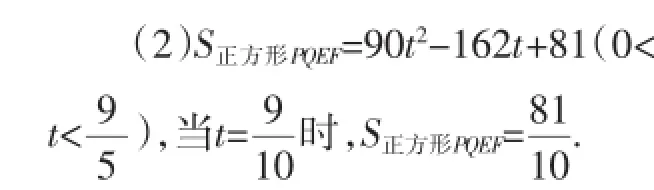
图8

（3）如图8，建立平面直角坐标系，AP=CQ=5t，AM= 4t，PM=3t.作PM⊥AC于点M，EN⊥AC于点N，可证△PMQ≌△QNE，得PM=QN=3t，MQ=EN=9-9t，HQ=5t，则直线HQ、GC、HG的解析式分别是x=9-5t、x=9、y=5t，点E、F、P的坐标分别是（9-2t，9-9t）、（7t，9-6t）、（4t，3t）.当点E（9-2t，9-9t）在正方形QCGH的边上时，有9-2t=9-5t，9-2t=9，9-9t=5t，其中符合题意的只有一解；当点F（7t，96t）在正方形QCGH的边上时，有9-6t=5t，9-5t=7t，7t=9，其中符合题意的解有；当点P（4t，3t）在正方形QCGH的边上时，有9-5t=4t，9=4t，3t=5t，其中符合题意的只有一解t=1.

五、圆

图9

（1）直接写出M、N两点的坐标（用含t和a的代数式表示）；

（2）连接AM，若经过时间t，存在△AOM与△CMN能够相似，求出t和a的值；

（3）当a=5时，以N点为圆心，MN为半径作⊙N.请直接写出在运动的整个过程中，⊙N与矩形ABCO的其中一边所在直线相切时t的值.

分析：本题是2016年浙江省衢州市中考调研卷的压轴题，笔者参与批改.本题第（1）问的得分情况较好，第（2）问有部分学生漏掉一个答案，第（3）问，笔者所批改的所有试卷当中，少部分学生能得到两三个答案，满分卷只有十来份.究其原因，⊙N的圆心N在运动，半径MN的长度也在发生变化，尤其是“⊙N与矩形ABCO的其中一边所在直线相切”，情况较多，给学生的画图分析带来很大的困难，导致比较优秀的学生答不完整.根据“直线与圆的相切的判定定理”，当d=r时，即圆心N到矩形四边所在直线的距离等于MN的长度时，就能完成第（3）问的解答.运用解析法，能很好地做到这一点.

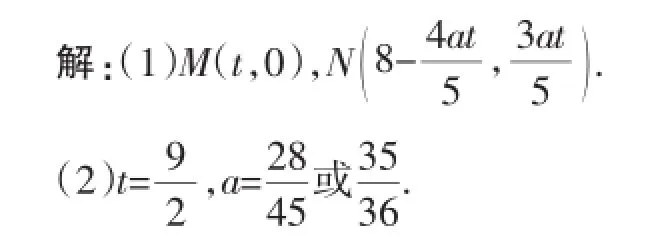
（3）当a=5时，M（t，0），N（8-4t，3t），MN2=（8-5t）2+（3t）2=34t2-80t+64.

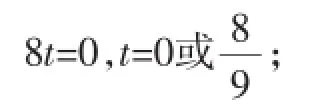
④当⊙N与AB相切时，MN2=（6-3t）2，25t2-44t+28=0，方程无实数根.

通过用解析法解决上述几种动点类型的存在性问题可以看出，当由点、线的运动，导致整个图形发生变化，很难画出符合题意的图形时，解析法通过“化动为静”、“化繁为简”可以很好地帮助学生解决动态问题.

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2.刘金英，张义民.重联系·重思想·重素养：2015年中考数学试题“图形与坐标”专题命题分析［J］.中国数学教育（初中版），2016（1-2）.

3.邓达，余献虎.巧用动态定位分析突破动点分类难题［J］.中国数学教育（初中版），2015（7-8）.

4.叶先玖.经历动态过程，还原思维历程——以一道几何题的解答为例［J］.中学数学（下），2016（2）.

5.奚喜兵.谋定而后动：几何动点问题的解决策略［J］.中学数学（下），2015（10）.H