小议外延知识教学实践——以特殊不等式解法探索为例
☉江苏张家港市凤凰中学 杨维娟
小议外延知识教学实践——以特殊不等式解法探索为例
☉江苏张家港市凤凰中学杨维娟
众所周知,初中数学存在一定的考查知识外延化,即以教材中的基本知识为本,扩散辐射到一定难度的外延知识.这些外延知识的学习依赖于探究性教学的实践,依赖于教师给出的教学设计.有时常常听到同行抱怨中考应试中,哪些知识不在考纲范围内、超纲、不要求等,笔者认为这些想法并不可取,只要是可以通过已经掌握的知识解决的新知识,都不属于超纲范围,因此加强数学外延知识的教学成为优秀学生更上层楼的关键.
如何设计外延知识的教学呢?如何梳理相关的外延性知识呢?既需要多年教学经验的总结,也需要自身对于问题新视角的思考与开发.笔者以特殊不等式解法为例,进行合理的设计与开发.解不等式是学生必须掌握的工具性知识,是初中数学必考之重点,其联系着各种数学知识,体现着知识的桥梁作用.随着教育的改革和创新,对这部分知识的考查要求也随之加大.在教改和课改的大浪潮中,初中不等式这部分知识点正不断地与高中“不等式的解”接轨.在题目中它常常会结合绝对值和根式等与之相关的内容来考,使题目的难度加大.考生对于这类大难度的题无从下手,却苦于无参考资料.下面将比较系统地总结该类特殊不等式的题型,并且给出比较完善的解法,以供考生和同行参考.
外延知识教学方向一:含有绝对值符号的不等式的解法
类型一:形如|ax+b|≤c或|ax+b|≥c(a、b、c为实数,且a≠0且c≥0).
问题1:解不等式:(1)|2x+1|>5;(2)|2x+1|<5.
分析:(1)由题意,一个整式的绝对值要大于5,有两种情况,一是这个整式的值大于5,另一个是这个整式的值小于-5.这样就可以把这个不等式转化成解两个一般的不等式,从而求出答案.(2)一个整式的绝对值要小于5,即这个整式的值在-5到5之间,也就转化为解一个一元一次方程了.
解析:(1)依题意,可得2x+1>5或2x+1<-5,解得:x>2或x<-3.
(2)依题意,可得-5<2x+1<5,即2x+1>-5且2x+1<5,解得-3<x<2.
类型二:形如|x+a|≥|x+b|或|x+a|≤|x+b|(a、b为实数).
问题2:解不等式:(1)|x+2|≥|x+1|;(2)|x+2|≤|x+1|.
分析:(1)根据绝对值的定义,不等式可变形为|x-(-2)|≥|x-(-1)|,它表示点x到点-2的距离大于或等于点x到点-1的距离,再通过数轴可以分析出答案.(2)与上面的同理,也能得出答案.
解析:(1)不等式可变形为|x-(-2)|≥|x-(-1)|,由绝对值的定义可得x≥
(2)不等式可变形为|x-(-2)|≤|x-(-1)|,由绝对值的定义可得x≤
提示:绝对值是初中数学中的重要概念,将绝对值与不等式结合,赋予了不等式全新的解决方式.学生能解决诸如ax+b>c的类型,也能理解|x|>a的几何意义,将两者结合产生的带有绝对值符号的不等式成为初中考纲之内知识的延伸,对这种外延知识进行恰当的教学,有助于学生站在更高的角度去理解绝对值,将整体性思想的介入体现得淋漓尽致,在思想层面提高了学生对于教材内知识的理解.
外延知识教学方向二:含有根号的不等式的解法
解析:(1)把不等式左、右两边分别平方,得2x+1>9,解得:x>4.
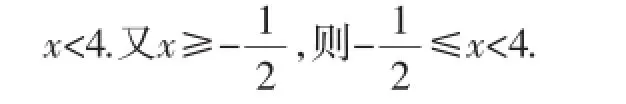
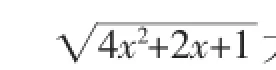
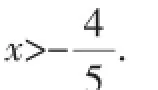
外延知识教学方向三:同时含有绝对值和根号的不等式的解法
分析:众所周知,绝对值和根式的值都是大于或等于0的,所以我们可以对不等式左、右两边分别平方,把绝对值符号和根号都去掉,去掉后发觉不等式左、右两边的4x2可以消去,从而转化为我们能够解的一元一次不等式.
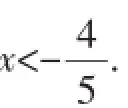
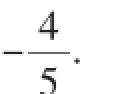
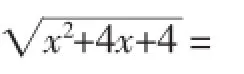
提示:这里笔者在原有方向一和方向二的基础上,将无理根式与绝对值融合,结合不等式,显然教师将学生对于不等式解决的难度提升到一个新的层面,基于初中数学最基本的三个知识点:绝对值、无理根式、不等式,将教材内的知识进行了外延拓展,大大提高了学生对于应试以上要求不等式的理解,也站在了更高的视角学会了对于数学知识的理解,加深了知识间相互穿插、融合使用的能力.当然,上述这些特殊的不等式的解答,需要在特定条件下来进行,而特定条件有时是很明显的,甚至是已知的,有时是隐蔽的,要解决此类题型还要靠我们在教学和研究中不断整理、总结,才能得心应手.
1.柴贤亭.数学教学中的问题设计[J].教学与管理,2012(10).
2.邵岳洲.试举由特殊方程或特殊不等式求解的几种情况[J].数理化解题研究,2013(9).
3.吴霞.不等式的特殊题型与解法[J].数理化解题研究,2014(5).Z

