贯通多解与预设追问：解题教学的备课视角——以武汉某区八年级把关题为例

☉江苏省如皋市高新区实验初中　陈亚东

贯通多解与预设追问：解题教学的备课视角——以武汉某区八年级把关题为例

☉江苏省如皋市高新区实验初中陈亚东

一、写在前面

郑毓信教授在代表著作《数学方法论入门》（见文1）开篇即指出：“在数学方法论的研究中，容易首先想到的一个问题是：与一般的科学家（如物理学家）相比，数学家们的思维方法是否有其独特的地方？对此，一种可能的回答是：数学家们特别善于使用化归的方法来解决问题.也就是说，在解决问题时，数学家们往往不是对问题进行直接的攻击，而是对此进行变形、使之转化，直到最终把它化归成某个（或某些）已经解决的问题.”

根据笔者多年的教学经验，在解题教学中，也需要向学生传递上述化归的策略.本文以一道八年级期末试题为例，讲解平移化归的策略在正方形为背景的考题突破中的应用，提供研讨.

二、考题及思路突破

考题（武汉市硚口区2016年八年级下学期数学期末考试第24题）如图1，已知正方形ABCD，点E在AB上，点G在AD上，点F在射线BC上，点H在CD上.

图1

图2

（1）如图2，若FG⊥DE，求证：BF=AE+AG；

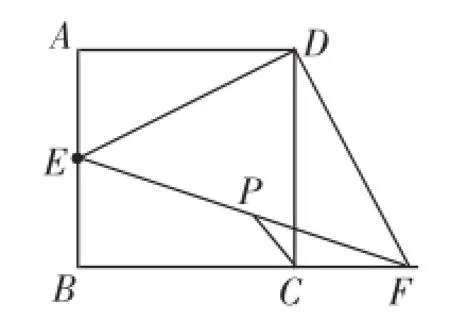
图3

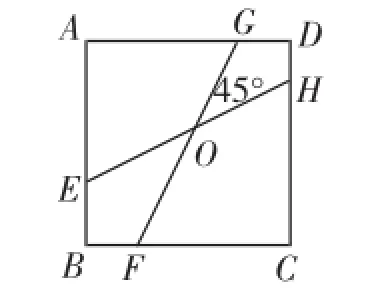
图4

（3）如图4，EH交FG于点O，∠GOH=45°，若CD=4，BF=DG=1，求线段EH的长.

思路突破：（1）考虑到条件FG⊥DE，可以选择构造GN⊥BC于点N（如图5），可利用全等三角形的性质（如△ADE≌△NGF）得NF=AE，而AG=BN，故“BF=AE+AG”得证.稍作反思，这条辅助线GN可以看作是将边AB向右平移所得，顺着平移的思考，还可得到如下不同的辅助线，如图6，过点A作AK∥GF交BC于点K，可证△ABK≌△DAE，得BK=AE，而AG=KF，故“BF=AE+AG”得证.

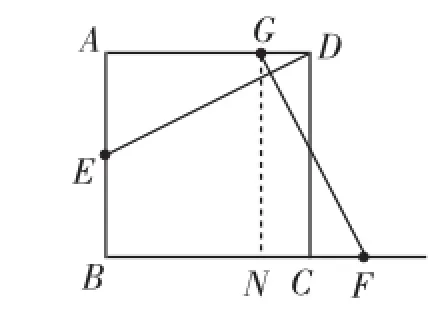
图5

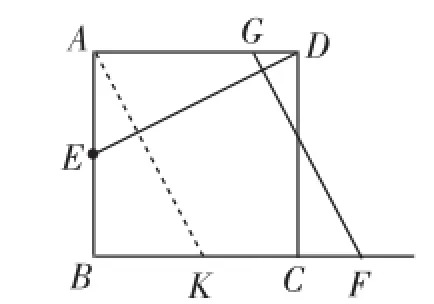
图6

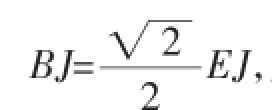
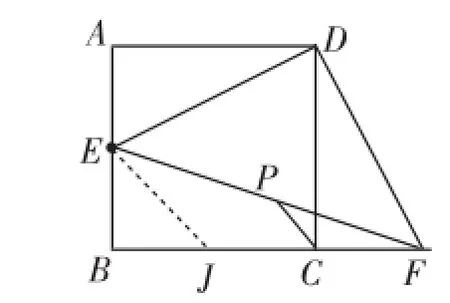
图7

图8

解后反思：如果没有顺利构造上述辅助线，也可以从洞察问题结构的角度进一步反思，比如，在图8中，连接BP，DP，根据对称性质，容易发现PC是∠BCD的平分线，发现∠BCP=45°，45°的出现也可启发思路.

（3）该题有一个重要的条件45°需要挖掘，如果盯住原图中的线段位置，也可以构造相关辅助线实现问题的求解，但如果受到上述平移变换的启发，可以将EH、FG分别平移到一个特殊位置，如图9，即点E、F都与顶点B重合.

图9

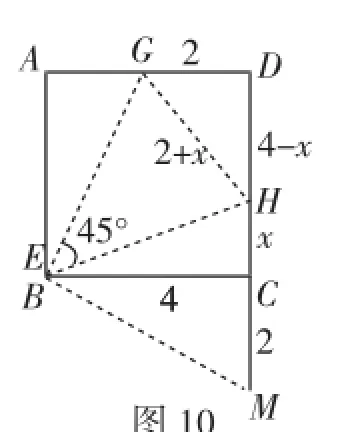
图10

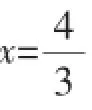
三、教学思考

由于该题呈现简约，但问题的生成自然、拓展适度、证法多样，是一道较有思维含量的几何题，也是一道较好的几何教学题例，以下再围绕该题的解题教学提出几点初步思考.

1.备课时要深刻理解例题的不同解法

众所周知，中学数学的课堂教学活动中，解题教学占有十分重要的位置，就当前的解题教学来看，不少课堂仍然停留在一题一解，答案揭示的较低层次，还缺少较有深度的解后反思，问题深层结构揭示的高度.这就要求，我们在备课时不仅要思考问题的思考贯通，更为重要的是要思考问题的尽可能多的解法或思路，这不仅是为了应对教学过程中及时理解学生可能的思考，更为重要的是，教者本人在贯通不同解题思路时，可以对比不同思路，并优选更能揭示问题本质的思路.而且能在深刻理解问题解法的情况下，进一步制作课件、预设追问，追求解题教学的成果扩大.

2.精心设计课件渐次呈现启发思考

由于现代化教学设备的普及，目前很多学校都配备了投影或白板设备，这对于数学解题教学来说作用是很大的，因为试题（特别是图形）的呈现可以通过现代化投影设置渐次有序呈现，帮助学生理解题意，做到基础不好的学生也能参与解题，促进他们理解初始问题，并继续向上攀登、挑战.以下就给出笔者关于上文中考题第（3）问制作的PPT的截图（如图11），提供分享.

图11

3.预设恰当追问促使问题拓展深入

解题教学备课时除预设学生可能的不同解法之外，作为解题教学的成果扩大，还需要思考例题的可能拓展或生长，对例题做出必要的反思回顾，在反思回顾阶段，可以引导学生积累问题结构，有时还可以通过引导学生做必要的追问，体会或感悟问题的结构.比如对于上文考题的解题教学，我们还可设计如下一些变式追问：

追问1：在（1）中，逆向思考，如果DE=FG，是否一定有DE⊥FG？说明理由.

预设意图：由位置上的垂直关系，可以推证等量关系，但是由等量关系却不一定能得到严格的位置关系.

追问2：在图3中，直线PC是否为正方形ABCD的对称轴？为什么？

预设意图：由图4的分析，可知直线PC平分∠BCD.这种追问主要是让学生积累和感悟基于轴对称的“以美启真”策略.

追问3：在图9中，连接GH，△GDH的周长是否为定值？如果是，求出定值；如果不是，说明理由.

预设意图：该三角形周长即为正方形边长的2倍.

讲评提醒：在上述追问下，可以引导学生理解所谓“把水倒掉”的数学家思维模式，即善于使用化归是数学家思维方式的重要特点.不在于这一个具体问题的解决，而在于让学生领悟如何转化、为什么想到转化等，即从知识的记忆走向方法的领悟.

四、写在最后

上文主要从考题的解法及解题教学角度给出阐释，如果从命题角度来看，我们也可提出一些商榷意见，比如，在限时考试的背景下，目前很多试卷容量较大，这时需要严格控制技巧高、辅助线不易获取的平面几何题的数量，因为根据笔者多年教学经验，一旦学生遇到没有练习过的平面几何题，如果需要构造一些不太常规的辅助线，则在考场上有限的时间内，是很少有学生能顺利贯通思路的，往往会造成一些考试分数的信度下降.

1.郑毓信.数学方法论入门［M］.杭州：浙江教育出版社，2006.

2.罗增儒.数学解题学引论［M］.西安：陕西师范大学出版社，2008.

3.【美】波利亚，著.怎样解题［M］.阎育苏，译.北京：科学出版社，1982.H