明晰内涵领悟本质——以一道中考数学试题的证明及其本质的挖掘为例

☉北京教育学院朝阳分院　白雪峰

明晰内涵领悟本质——以一道中考数学试题的证明及其本质的挖掘为例

☉北京教育学院朝阳分院白雪峰

学生的几何素养是指学生在解决具有一定背景的问题的过程中，面对不同形式的几何对象，以及在使用适当的几何知识和技能进行探究过程中所表现出的几何思维水平、几何推理能力和应用能力.［1］几何推理能力在国际数学教育界被一致视为基础且重要的能力之一，在平面几何教学中，教师要特别重视几何直观和多样表征对于学生几何学习的影响，关注图形直观对于学生理解几何推理过程的重要价值，从而不断发展学生的几何推理能力.［2］

下面笔者以2014年北京市中考数学第24题的证明及其本质的挖掘为例，谈谈通过改变问题已知条件，探求几何图形本质，拓宽几何思维空间，引导学生透过问题的证明和拓展过程，明晰几何问题内涵，领悟几何问题本质，以此发挥几何教学育人功能的实践与思考.［3］

一、原中考试题的解答及其分析

在正方形ABCD外侧作直线AP，点B关于直线AP的对称点为E，连接BE、DE，其中DE交直线AP于点F.

（1）依题意补全图1；

（2）若∠PAB=20°，求∠ADF的度数；

（3）如图2，若45°＜∠PAB＜90°，用等式表示线段AB、FE、FD之间的数量关系，并证明.

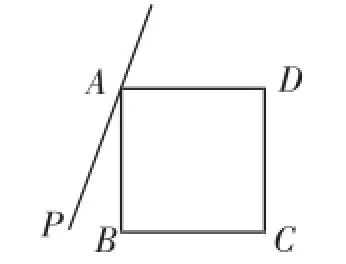
图1

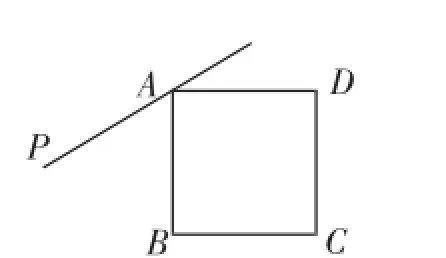
图2

本题的（1）和（2），利用轴对称图形、等腰三角形的性质等知识，是比较容易得到答案的，这两问的主要目的是让考生认识和熟悉试题的已知条件、图形特征，并为解决（3）铺路.本题重点是（3），需要先猜想出结论，然后还要证明结论的正确性，这也是本题的难点所在.直接解决（3），并挖掘图形和问题的本质特征，将问题进行变化和一般化推广.

解：（1）和（2）略.

（3）猜想：FE2+FD2=2AB2.

证明：如图3，连接AE、BF和BD.

由轴对称性质可得：

FE=BF，AB=AE=AD，∠ABF=∠AEF=∠ADF.

所以A、F、B、D四点共圆.

在正方形ABCD中，

在Rt△BFD中，

由勾股定理得BF2+FD2=BD2.

所以FE2+FD2=2AB2.

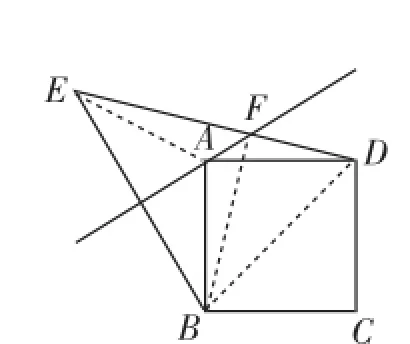
图3

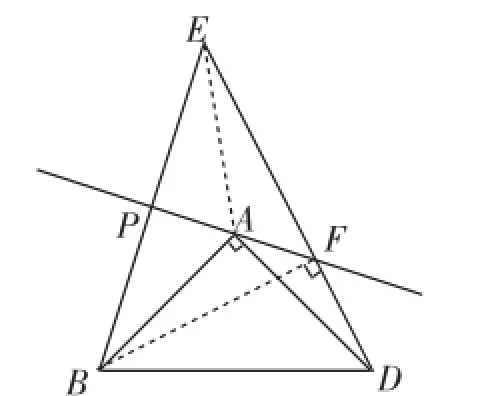
图4

点评反思：回顾（3）的证明过程，不难发现本问的结论只与正方形ABCD中的等腰直角△BAD有关，而与等腰直角△BDC无关，因此，可以去掉等腰直角△BDC，从而可以将图3变成图4.

笔者认为，在平时的几何教学中，教师还要进一步引导学生进行探究，将上述问题的已知条件弱化，其结论是否还能成立或结论会发生怎样的变化？

事实上，通过研究不难发现，我们可以将本问题变化到更一般的情形，即将已知条件中的△BAD为等腰直角三角形改变为△BAD为等腰三角形，原问题的结论只会发生细微变化，同样也是一个比较漂亮的结论.

二、原中考试题的变化

下面，我们先将等腰直角三角形变化为一个特殊的等腰三角形，即等边三角形，然后将其变化到一般的等腰三角形的情形.

变化问题1：

已知：在等边△ABD的外侧作直线AP，点B关于直线AP的对称点为E，连接BE，DE，其中DE交直线AP于点F.求证：FE2+FD2=AB2+FE·FD.

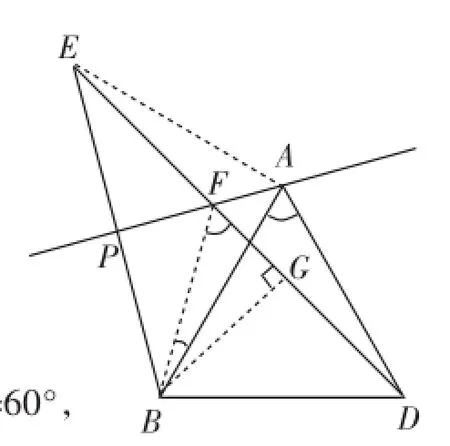
图5

证明：如图5，连接FB、AE.由轴对称性质可得：

FE=FB，AB=AE=AD，

∠ABF=∠AEF=∠ADF.

所以A、F、B、D四点共圆.

在等边△ABD中，∠BAD=60°，

AB=BD.

所以∠BFD=∠BAD=60°.

过点B作BG⊥FD于G.

在Rt△BGF中，∠BFG=60°，∠FBG=30°.

在Rt△BGD中，由勾股定理得：

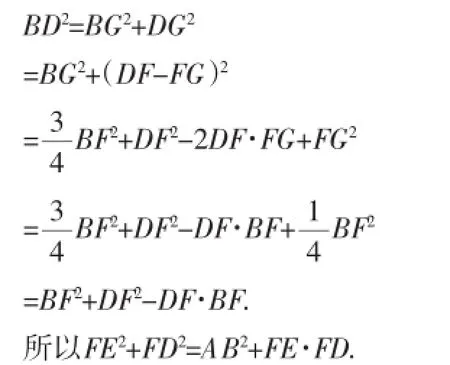
当△ABD为一般的等腰三角形时，则有下面的问题.

变化问题2：

已知：在等腰△ABD（AB=AD）外侧作直线AP，点B关于直线AP的对称点为E，连接BE、DE，其中DE交直线AP于点F.

求证：FE2+FD2=BD2+2FE·FD·cos∠BAD.

（为使结论简明，我们就不用AB表示BD了.）

证明：如图6，连接FB、AE.

由轴对称性质可得：

FE=BF，AB=AE=AD，∠ABF=∠AEF=∠ADF.

所以A、B、D、F四点共圆.

所以∠BFD=∠BAD.

在△FBD中，由余弦定理得；

BD2=BF2+FD2-2BF·FD· cos∠BFD.

所以FE2+FD2=BD2+2FE·FD· cos∠BAD.

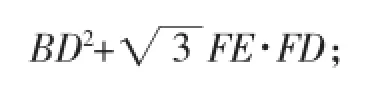
当∠BAD=60°时，FE2+FD2=BD2+FE·FD；

当∠BAD=90°时，FE2+FD2=BD2=2AB2；

当∠BAD=120°时，FE2+FD2=BD2-FE·FD；

……

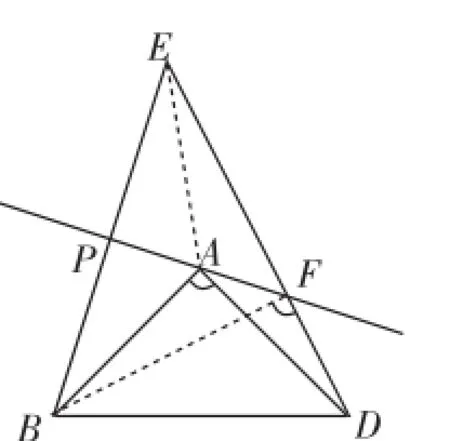
图6

从以上的特殊情况可以知道，原中考试题是上述特殊情况之一.

反思上述问题已知条件的改变过程可以看到，从正方形到等腰直角三角形，再到等边三角形，最后变化为等腰三角形，所得结论也随之更加一般化，但问题论证的基本过程和基本方法是一致的，其中的不变之处就是A、B、D、F四点共圆，只要能抓住这一问题解决的根本，也就掌握了本问题的实质.

初中平面几何中的推理证明既是教学中的重点也是难点，笔者认为，在平面几何学习中，学生最重要的任务是学会用科学、准确的数学符号语言正确地表达逻辑思维过程.因此，在课堂教学中，教师要通过精良的几何问题，培养学生通过图形直观发现问题的几何特征，正确运用图形记号、数学符号语言和逻辑推理的方法表达平面几何中的演绎推理过程.［4］从而指导学生掌握逻辑推理证明的方法，培养他们的数学思维能力，改变学生单纯模仿教科书上几何推理证明的学习现状，提高数学学科的直观想象和逻辑推理素养.

1.苏洪雨.学生几何素养的内涵与评价研究［D］.上海：华东师范大学，2009.

2.綦春霞，王瑞霖.中英学生数学推理能力的差异分析［J］.上海教育科研，2012（6）.

3.白雪峰，王敬如.追根溯源揭示本质——一道有背景的中考试题的证明和拓展［J］.中国数学教育，2015（5）.

4.刘京莉.学会用数学语言表达几何逻辑思维过程［J］.数学通报，2007（5）.Z