难题破解重思路，讲评预设问题串——一道“北京四中模考题”的思路与教学

☉江苏苏州工业园区青剑湖学校　丁志国

难题破解重思路，讲评预设问题串——一道“北京四中模考题”的思路与教学

☉江苏苏州工业园区青剑湖学校丁志国

初三复习备课期间，我们常常会关注来自不同地区的模考试题，并将一些复习过程中的“盲点”试题类型引入自己的教学中进行补充和拓展，这在复习工作中显得十分重要.最近一次家庭作业中，笔者给部分优秀学生挑选了网上传播的一道北京四中模考难题，为了追求较好的讲评效果，笔者进行了相关备课准备，取得了较好的解题教学效果.本文梳理该题的思路突破与讲评时的问题串预设，供研讨.

一、考题思路突破与反思回顾

考题：（2015～2016学年北京市第四中学初三下学期3月模考卷，第29题）如图1，平面直角坐标系xOy中，在半圆O与其直径所构成的封闭图形N中，有一个小圆⊙P分别与直径和半圆弧相切.当⊙P的直径改变时，其圆心P的位置也会发生变化，点P的所有可能的位置所组成的曲线（不包括A、B两点）称作图形N的“内切轨迹”，如图中的曲线.在平面直角坐标系中还有一条动直线y=kx+b（k≠0）.已知OA=OB=1.

（1）若⊙P同时也与y轴相切，则P点的坐标为________；

（3）当k的值一定时，若使直线y=kx+b与图形N的“内切轨迹”只有一个公共点的b的取值范围为m≤x≤n的形式，求k的取值范围.

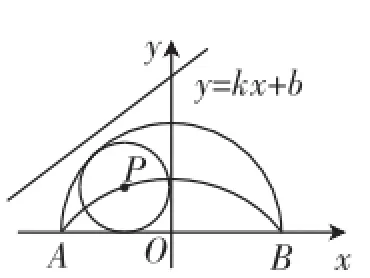
图1

（一）思路讲解

解题之前的必要准备是先读懂新定义，⊙P与x轴相切，⊙P与半圆相切，可以初步理解点P的位置（不含A、B），并且这些点P形成“内切轨迹”.

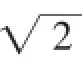
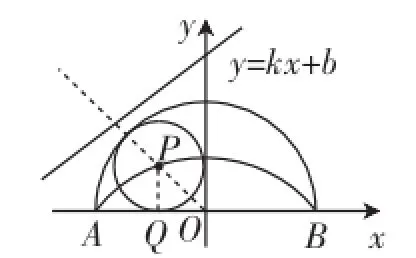
图2

图3

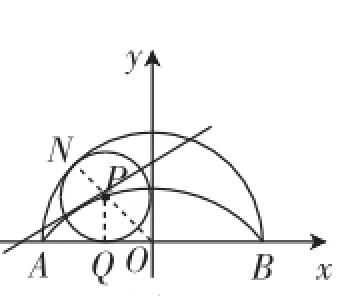
图4

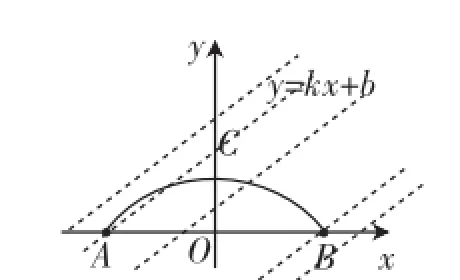
图5

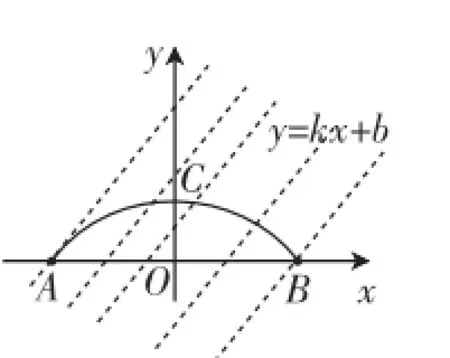
图6

让我们调整草图，构造图6，分析临界位置，

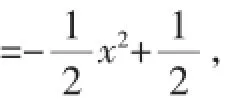
如图6，当k＞1时，可满足题意，因此，当k＞0时，k满足k≥1.

根据对称性，当k＜0时，k满足k≤-1.

综上，k的取值范围：k≥1或k≤-1.

（二）解后反思

从上面的求解思路来看，有好几处解题关键.

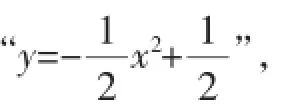
二、解题教学的“问题串”设计

以下提供系统问题串，在这些问题串的引导下帮助学生理解和思考模考题.

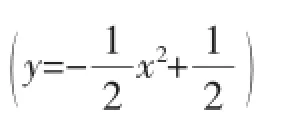
问题3：⊙P是否可能与y轴相切？如果可能，求点P的坐标；如果不能，说明理由.

问题4：试分析图形N的“内切轨迹”是否有最高点.如果有，求出这个最高点的坐标；如果没有，说明理由.

问题7：当k=2时，若直线y与图形N的“内切轨迹”只有一个公共点，求b的取值范围.

问题8：当k=-3时，若直线y与图形N的“内切轨迹”只有一个公共点，求b的取值范围.

问题9：当k的值一定时，若使直线y与图形N的“内切轨迹”只有一个公共点的b的取值范围为m≤x≤n的形式，求k的取值范围.

设计意图：通过上述问题串，让学生在启发式问题的引导下学会思考，学会从特殊到一般获取思路、解决考题.

三、结束语

初三复习阶段，试卷讲评课是一种重要的课型，如何突出重点，解析难点，把力用在点子上，是值得每个备考教师认真思考的课题，我们期待通过对一道模考难题的思路突破和解题教学的问题串设计，提供一种备课的思路，抛砖引玉，敬请批评指正.

1.鲍建生，顾泠沅，等.变式教学研究［J］.数学教学，2003（1，2，3）.

2.郑毓信.善于提问［J］.人民教育，2008（19）.

3.郑毓信.善于优化［J］.人民教育，2008（20）.

4.刘东升.对时育物，有效追问——浅论初中数学课堂教学中的追问艺术［J］.中学数学教学参考（中），2012（4）.Z