多思少算：一种值得追求的解题教学策略

☉江苏如东县实验中学　徐　亮

多思少算：一种值得追求的解题教学策略

☉江苏如东县实验中学徐亮

解题教学应该追求什么？文1给出了一种很好的思路：追求解题成果的深化与扩大.笔者在认同上述观点的同时，感觉在解题教学中应该还有一种追求：多思少算.虽然《义务教育数学课程标准（2011年版）》（下面简称《课标（2011年版）》）把运算能力作为十大核心素养之一，但是这应该是“数式运算类”试题追求的方向，即使这样，数式运算也应该做到“从遵守规则到追求简化”，而“追求简化”正是“多思”的一种体现，其他题目更是应该把考查的方向放在对学生思维能力训练的层面上，加深思维层次，加大思维含量.下面结合在教学过程中的实践，简单谈两点思考，不当之处还请各位专家和同行批评指正.

一、案例两则

案例1：加深思维层次.

原题：如图1，在四边形ABCD中，AB=AD=6，AB⊥BC，AD⊥CD，∠BAD=60°，点M、N分别在AB、AD边上.若AM:MB=AN:ND=1:2，则tan∠MCN的值为_______.

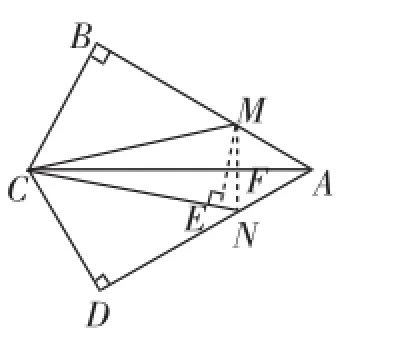
图2

解法1：连接MN交AC于点F，过点M作ME垂直于CN于点E（如图2）.

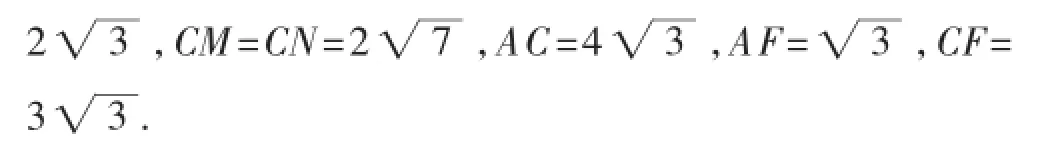
解法2：连接MN交AC于点F，过点M作ME垂直于CN于点E（如图2）.

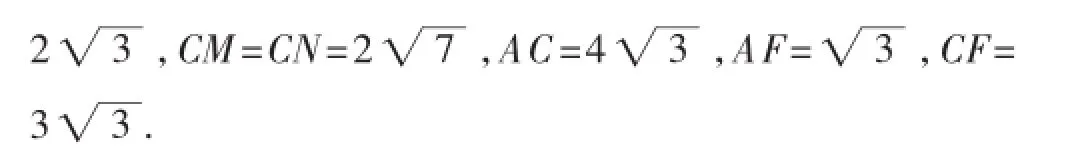
因为∠EMN+∠MNE=90°，∠FCN+∠CNF=∠FCN+∠MNE=90°，所以∠EMN=∠FCN，所以△EMN∽△FCN.

评析：解法2与解法1比较，明显减少了许多计算量，笔者认为这是思维层次加深的原因.两种解法添加了同样的辅助线，解法1主要结合面积相等和勾股定理的知识对问题给出了解答；而解法2则加深了一步，发现了图中存在的一对相似三角形，进而结合相似三角形的相关知识解决了问题.日本著名数学家米山国藏在其名著《数学的思想、精神及方法》中指出：“数学是一步一步往上走的”，而初中阶段对直角三角形的相关知识（勾股定理、直角三角形相似、锐角三角函数）的学习正是遵循上述论述的，在教学过程中，应该引导学生体会这种逻辑顺序和逐层加深的思想.

案例2：加大思维含量.

原题：如图3，在Rt△ABC中，AB=2，BC=1，∠A=30°.请你添加喜欢的辅助线，求出tan15°的值.

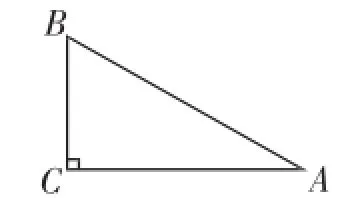
图3

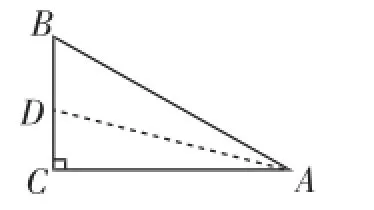
图4

解法1：如图4，作∠A的角平分线交BC于点D，则∠CAD=15°.

解法2：如图5，延长CB到点D，使CD=AC，则∠BAD= 15°，过点B作BE垂直AD于点E.

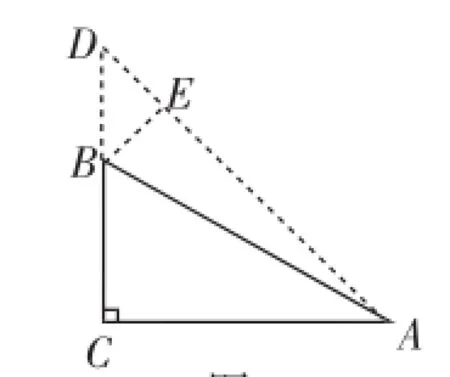
图5

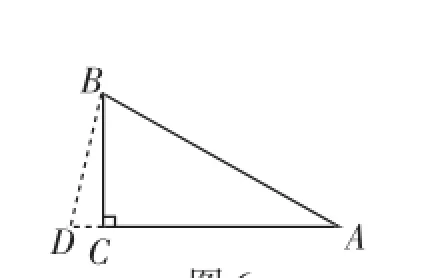
图6

解法3：如图6，延长AC到点D，使AD=AB，则∠CBD= 15°.

解法4：如图7，延长CA到点D，使AD=AB，则∠BDC= 15°.

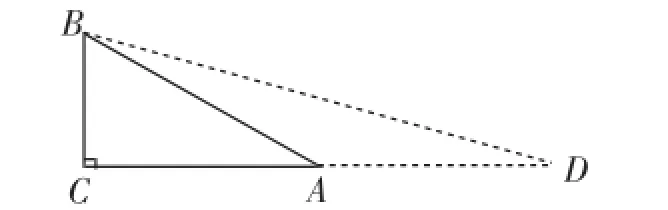
图7

评析：解法1—解法4都遵循了共同的解题思路，即：构造15°的角，然后构造直角三角形，最后在直角三角形中应用锐角三角函数正切的定义进行求解.可以看出解法1中辅助线的添加是最容易想到的，但是这其中需要用到三角形中角的平分线的一个性质，对于初中生而言是很难顺利求解的；解法2和解法3的辅助线的添加方式有点儿类似，都利用了等腰三角形的知识，相比较而言，解法2的辅助线更容易想到，但是在求解过程中运算量非常大，甚至涉及了无理数的开平方，对初中生而言是有难度的，而解法3的辅助线虽然不易想到，但是一旦添加了这样的辅助线，问题便会顺利解决，因为基本上没有什么计算涉及；解法4的辅助线应该是最不易想到的，利用了三角形外角的性质，通过简单计算问题便会迎刃而解.比较上述4种解法，可以发现随着思维含量的逐渐加大，解决问题过程中涉及的计算量越来越少，进而问题解决起来便越来越自然、越来越顺利.

二、两点思考

1.多思少算需要中考命题导向的指引

中考试题是课堂教学的指挥棒、风向标.特别是《课标（2011年版）》实施以来，由于其对运算能力的重视，在中考试题中出现了大量的关注计算水平的试题，可以说这是一种好的趋势，但是这种趋势现在有点儿“走偏”的感觉，学生的运算能力有了一定的提高，但是思维能力却不见好转.学生真正走向社会，对其发生作用、伴其一生的应该是在数学学习中习得的思维能力，只有在重视学生运算能力的同时，更加重视对学生思维能力的培养，我们的数学教育才可能真正起到应有的作用.

2.多思少算需要一线教师积极践行

在课堂教学中，有的教师向学生灌输“不管用什么方法，只要能解决问题”即可，殊不知这是一种极其功利的心态，缺少了对学生思维能力的培养.在课堂教学中，教师应该注意一题多变、一题多解，在多种解法中寻求最优的解法，引导学生体会不同的思维层次对解决同一问题带来的不同效果，这样学生才可能真正体会到解题的乐趣，才能培养学生欣赏的眼光，才能使学生走出“题海”，真正地爱上数学，这正是现阶段解题教学中所缺失的，必须引起一线教师的足够重视，进而在课堂教学中积极践行，进而实现解题教学的最大价值.

1.朱月祥.追求解题成果的深化与扩大［J］.中学数学教学参考（中），2015（11）.

2.刘东升.初中数学是这样学好的［M］.杭州：浙江大学出版社，2015.Z