奇、偶数项各有特点的数列求和问题的解决策略

◇　山东　王希刚

(作者单位：山东省章丘市第一中学)



奇、偶数项各有特点的数列求和问题的解决策略

◇山东王希刚

“数列求和”问题是数列部分的重点知识,是高考和模拟考的必考内容,这类题目的设计灵活、解法多样,但是,不管用什么方法求解,最终都会归结为等差、等比数列的求和问题．因此,抓住等差、等比数列求和所需的基本信息——首项、公差、公比、项数、末项,这类问题将很好得到解决．

奇、偶数项各有特点的数列求和问题,是近几年考查的一个热点问题,但是,同学对这类问题处理得并不好.下面就此问题的解决策略进行探讨．

策略1抓住基本信息,直接求解．

采取这种方式,要使学生明确:对于n的不同取值,数列的基本信息不同．因此,需要分n为偶数和n为奇数2种情况分类讨论处理．

当n为偶数时,奇数项和偶数项各有n/2项,奇数项的首项为1,末项为第n-1项,即6(n-1)-5=6n-11,偶数项的首项为4,公比为4．所以

综上可得

这种处理方式需要同学们明确当n为奇数和n为偶数时数列的基本信息.此类问题涉及的信息量比较大,极易出现差错．

策略2由Sn(n为偶数)→Sn-1(n为偶数)→Sn(n为奇数)→得解．

由策略1可知,当n为偶数时,

所以

令t=n-1(t为奇数),则n=t+1,所以

这种处理方式先解决当n为偶数时的和,然后减去第n项,得到前n-1项的和,其中n-1为奇数.利用函数知识:由f(x-1)的表达式→f(x)表达式,可实现由Sn-1(n为偶数)→Sn(n为奇数),从而得解．

策略3S2n→Sn(n为偶数)→Sn-1(n为偶数)→Sn(n为奇数)．

由条件可知前2n项中,奇数项、偶数项各有n项,奇数项的首项为1,末项为第2n-1项,即6(2n-1)-5=12n-11,偶数项的首项为4,公比为4．所以

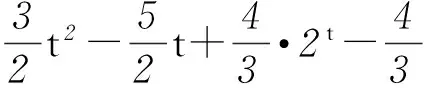
这种处理方式中数列的基本信息易得,涉及的基本信息全是整数,因此,求S2n的计算量比直接计算n为偶数的Sn的计算量小,而借助函数知识,由S2n→Sn(n为偶数)的运算也较简单．

这类问题以等差、等比数列求和为载体,是最基本的考查方式,也可以裂项求和、错位相减求和为载体,提高题目的难度,更加综合地考查数列求和问题．只要掌握了上述例题的基本处理方式,对于变式题目,也能轻松解决．

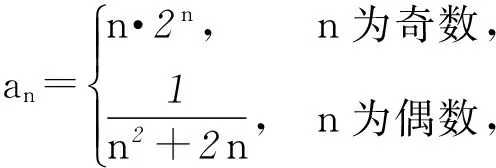
综合比较,此题的求解可以采取策略3中的方法,以减少题目的计算量．

将奇数项和偶数项分别求和得

S奇=1·21+3·23+…+(2n-1)·22n-1,

4S奇=1·23+…+(2n-3)22n-1+(2n-1)22n+1,

-3S奇=2+24+…+22n-(2n-1)·22n+1=

所以

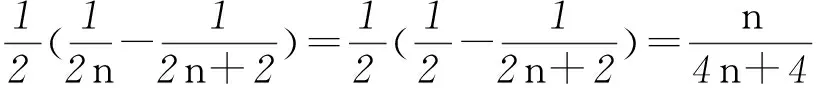
所以

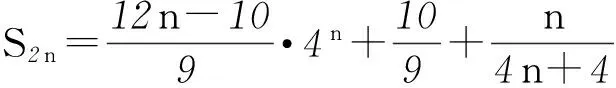
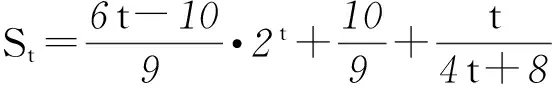
通过例题的3种处理策略可以看出,不管是数列的基本信息、求函数表达式的知识,还是变式中的错位相减法求和、裂项求和,都是基础知识,如果同学们对基础知识的掌握足够牢固,明确这类题目的处理策略,不难解决此类问题.这需要教师在平时的教学中下足功夫,帮助学生打好基础,这样很多问题将迎刃而解．

(作者单位：山东省章丘市第一中学)