高考几何证明选讲透视

◇　山东　葛学清

(作者单位：山东省日照第一中学)



高考几何证明选讲透视

◇山东葛学清

1　高考展望

相似三角形与射影定理考查的重点是利用平面几何中三角形相似、直角三角形的射影定理等相关知识解决平面几何中线段关系等问题,一般以小题的形式出现,试题难度为低档;直线和圆的位置关系考查的重点是利用相交弦定理、切割线定理、圆周角定理等相关知识解决平面上与圆有关的角、线段等问题,一般以解答题形式出现,多是计算与证明考题,试题难度为中档,考查逻辑推理能力．

有鉴于此,备考中要熟练掌握多种题型,以不变应万变,但要注意训练题的难度．

2　常考题型

2.1相似三角形及射影定理

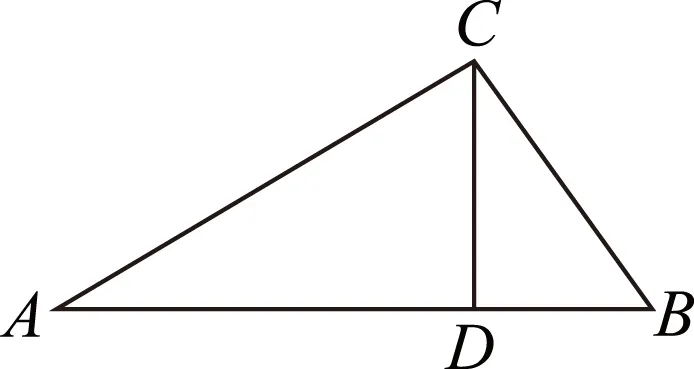
图1

审题视角本题根据直角三角形相似的判定,可求得CD=6,进而可得AC∶BC的值; 另外,直角三角形的射影定理是相似三角形的性质在直角三角形中的一个经典应用,在类似问题中应用射影定理十分简捷．

方法2因为∠ACB=90°,CD⊥AB于D,所以由射影定理得AC2=AD·AB,BC2=BD·AB.

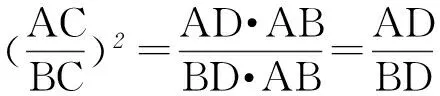
备考策略在使用直角三角形射影定理时,要学会将“乘积式”转化为相似三角形中的“比例式”;证题时,作垂线构造直角三角形是解直角三角形常用的方法．

图2

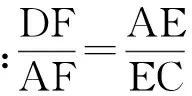
答案及提示由三角形的内角平分线定理和射影定理证得．

2.2直线和圆的位置关系

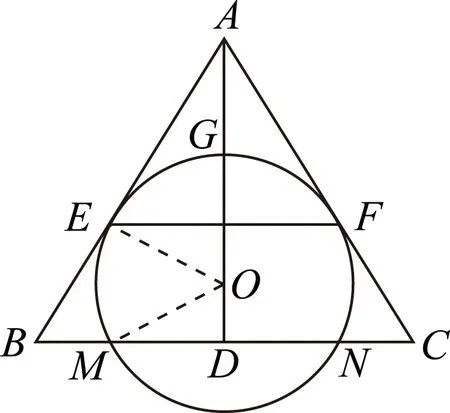
图3

(1) 证明EF∥BC;

审题视角(1) 通过AD是∠CAB的角平分线及圆O分别与AB、AC相切于点E、F,利用相似的性质即得结论;

(2) 通过(1) 知AD是EF的垂直平分线,连接OE、OM,则OE⊥AE,利用S△ABC-S△AEF计算即可.

(2) 由(1)知,AE=AF,AD⊥EF,所以AD是EF的垂直平分线.又EF为⊙O的弦,所以O在AD上,连接OE、OM,则OE⊥AE.由AG等于⊙O的半径得AO=2OE,所以∠OAE=30°,所以△ABC和△AEF都是等边三角形.

备考策略应用相交弦定理、切割线定理解决问题时,要注意相似三角形知识与圆周角、弦切角、圆的切线等相关知识的综合应用．

图4

变式如图4,AB是⊙O的直径,G是AB延长线上的一点,GCD是⊙O的割线,过点G作AG的垂线,交直线AC于点E,交直线AD于点F,过点G作⊙O的切线,切点为H.

(1) 求证:C、D、E、F四点共圆;

(2) 若GH=6,GE=4,求EF的长.

答案及提示(1) 略;(2) EF=5.

2.3易错点:三角形相似与圆的交会问题

图5

证明:

(1) AC·BD=AD·AB;

(2) AC=AE.

审题视角(1) 根据待证等式可将各边回归到△ACB、△DAB中,再证2个三角形相似;

(2) 本问可先证明△EAD∽△ABD,再结合第(1) 问结论得证．

综合(1)的结论知,AC=AE.

备考策略证明本题第(2)问时易失分点:1) 想不到证明△EAD∽△ABD而无法解答; 2) 没有应用第(1)问的结论而无法证明结论成立.

防范措施: 1) 证明等积式成立,应先把它写成比例式,找出比例式中给出的线段所在三角形是否相似,若不相似,则进行线段替换或等比替换; 2) 在有多个结论的题目中,如果结论带有普遍性,已经证明的结论,可作为证明下一个结论成立的条件使用; 3) 在解决相似三角形时,一定要注意对应角和对应边,否则容易出错.

(作者单位：山东省日照第一中学)