小物和小理的物理对话录(35)——光的衍射条纹

◇　北京　刘　铭　蒋炜波　孟卫东(特级教师)

(作者单位：清华大学附属中学)



小物和小理的物理对话录(35)

——光的衍射条纹

◇北京刘铭蒋炜波孟卫东(特级教师)

前言:小物和小理是2名普通的高中生,他们酷爱物理,在学习高中物理的过程中,小物经常向小理提出许多刁钻而有趣的物理问题,了解他们的故事也能让你的物理达到新的高度．

1　对话录

小物:通过之前折射率的推导,我才发现惠更斯原理居然这么好用,而且还能够用惠更斯原理直接推导解释反射定律以及全反射现象,太神奇了!

小理:是的,虽然惠更斯原理没办法解释光的本质,但是它从波动角度出发,还是比较好地解释了折射和反射现象,它还能够定性地解释衍射现象．

小物:的确是,只要想到最前沿的振动质点是一个新的波源,那么波源产生的波将向各个方向传播,就能够解释为什么波能够绕到障碍物后面继续传播了,但是好像没办法解释障碍物尺寸和衍射明显程度的关系．

小理:是的,所以说是定性解释,说明惠更斯原理还是不够完美．

小物:说起来,我们刚刚学过波的干涉现象,还得到了干涉条纹的分布规律,而同时书上又说波通过狭缝的时候能够看到衍射现象,也给出了衍射条纹分布图,但是并没有给出具体的条纹分布规律,如果咱们可以弄清衍射条纹的分布规律,就能够补充惠更斯原理了呀!

小理:说得容易,衍射条纹也有亮条纹和暗条纹,怎么确定亮暗条纹的位置呢?你有想法吗?

小物:我这不是找你讨论来了嘛,我也暂时没想法,但老师不是说只要多加思考肯定能找到办法.

小理:我想想看…….

2　小理的思考

衍射现象也出现了亮条纹和暗条纹,根据干涉条纹的规律,亮暗条纹是由于不同相位的波在某处叠加造成的,而相位关系是由波程差决定的．那么我们能不能假设衍射现象中的亮暗条纹也是由于波的叠加造成的呢?如果假设成立的话就能够通过波程差来寻找衍射条纹的位置了!

2.1光的双缝干涉条纹

如图1所示，激光垂直照射到双缝S1、S2上,双缝S1、S2相当于2个新的光源,而且相位相同(即振动同步),且2个光源发出的光各自传播到屏幕上的P1点,各自走过的路程(即光程)为r1和r2,如果想要光屏上P1处出现亮条纹,根据波的叠加原理要求光程差r2-r1必须为半波长的偶数倍(或者波长的整数倍),即Δx=r2-r1=nλ.

图1

取P1M=P1S1=r1,因为屏幕到双缝的距离L很大,远远大于双缝的间距d,即r1和r2均远大于d,因此可以近似认为S1M⊥P1M,这样光程差为

Δx=r2-r1=S2M=dsinθ=nλ.

与此同时,光屏上P1点到光屏中心P的距离x=Ltanθ. 在角度很小的时候,可以近似认为

sinθ=tanθ,于是

于是我们得到干涉亮条纹在屏幕上的位置

据此我们发现双缝干涉的亮条纹间距相同,所以我们说干涉条纹是等间距均匀分布的,当然这也仅仅限于屏幕中心部分,因为只有屏幕中心部分才满足角度很小，使得sinθ=tanθ成立．

2.2光的单缝衍射条纹

根据干涉条纹的形成过程我们可以发现,只要出现亮暗条纹分布,则一定是出现了波的叠加,使得在空间中出现了叠加加强和叠加减弱的区域.在这样的认知前提下,我们也可以认为衍射亮暗条纹的出现也是由于光波的叠加导致的.

图2

为了方便推导,我们借助干涉现象来解释衍射现象,如图2所示，我们将单缝分成上下2部分S1和S2,上下2部分的光线一一对应,比如上部分的最上方光线和下部分的最上方光线对应,以此类推．因为实验得到的衍射条纹并不是等间距分布,而且屏幕中心位置P一定是衍射亮条纹,因此我们在这里首先寻找中心亮条纹的边界,即第1级暗条纹的位置P1．

暗条纹在这里的含义是单缝上下2部分所有的对应光线在P1处都是干涉相消,导致屏幕上接收不到光线产生暗纹.我们先研究S1和S2最上方对应光线干涉相消的条件,取P1M=P1S1=r1,因为屏幕和单缝的距离L很大,远远大于单缝的宽度d,即r1和r2均远大于d,因此可以近似地认为S1M⊥P1M,2条光线的光程差为

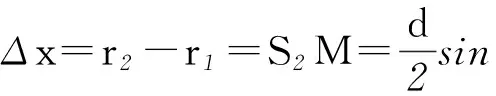
为了使得2条光线干涉相消,必须满足光程差为半波长的奇数倍.我们计算第1级暗条纹的位置,因此时光程差为半波长的1倍,于是得到

在衍射现象中,明显衍射的条件之一是障碍物的尺寸和波的波长能够相比,这样使得上述结果对应的θ角不像双缝干涉中的那么小,因此一般不再认为sinθ=tanθ,因此暗纹P1的位置不再使用距离P1P来标定,而是使用θ角直接标定．与此同时也可以看到，当障碍物的尺寸等于波长的时候,即d=λ时,θ=90°,衍射条纹将分布在整个光屏上,当然最主要的光仍然分布在正中央,其他地方的光非常弱以至于不可见．

同样的方法,我们可以继续标定第2级暗纹的位置．我们很容易想到当上述光程差为半波长的3倍的时候,在屏幕上也会得到暗纹,即

这的确是一条暗纹的位置,但这并不是第2级暗纹的位置,因为在这条暗纹和第1级暗纹中间还有1条暗纹．我们换个角度考虑,继续使用上述方法,我们将单缝的上下2半部分各自再分成2部分,即将单缝分成4部分,如图3所示.

图3

相比之下P2更加靠近第1级暗条纹,因此这是衍射的第2级暗条纹,而之前的那一条纹为第3级暗条纹．因此衍射暗条纹的分布为

n为暗条纹的级数．这样我们就得到了单缝衍射的条纹分布规律,可见衍射条纹确实不是等间距的,这一点和干涉条纹区别很大．

除了条纹分布之外,不同条纹的亮暗程度也是不一样的,干涉亮条纹的亮度几乎相同(在屏幕中央附近的干涉加强亮条纹),而衍射亮条纹中中间亮条纹最亮,其他亮条纹则相对暗了很多,因此在测量光的波长的实验中我们采用了干涉现象,而非衍射现象．

故事到了最后,小物又给小理提出了一个问题:衍射光栅的条纹分布原理和干涉条纹的分布原理一样吗?是否也能够用上述方法解释呢?

(作者单位：清华大学附属中学)