明晰七个"如何"回归教学本质---"等可能性"教学观评有感

江苏省泰州市教育局教研室　钱德春

明晰七个"如何"回归教学本质
---"等可能性"教学观评有感

2015年11月,江苏省教研室成功举办了初中数学青年教师优秀课评比活动.比赛课题之一是苏科版义务教育数学教科书九年级"4.1等可能性",笔者有幸担任了这一课题的评委工作.这是一节概念课,不少选手从理解数学、理解学生、理解教学的角度精心设计教学活动,恰当地处理课堂教学的几大关系.活动可谓百花齐放、亮点纷呈,展示了江苏省初中数学课堂教学改革的成果,发挥了良好的示范效应,一批优秀初中青年数学教师脱颖而出.在感受了选手风采、感动于选手精神的同时,也发现一些有待探讨的问题:如何准确定位教学目标,如何使情境设计更具科学性,如何突破教学难点,如何让活动指向数学思维,如何以问题驱动数学思考,如何处理好教师与学生的关系,如何体现良好的价值导向……这些问题,归根结底是如何回归数学课堂教学本质的问题,非常值得我们去研究.本文拟结合比赛的教学案例,通过对七个"如何"的解析,谈谈笔者对相关问题的思考.

一、如何准确定位教学目标

教学目标是一节课的灵魂,凸显了教者对教学内容的理解深度,统领着教学的方向、高度、广度、进度.选手A将"等可能性"的教学目标确定为:(1)知识与能力目标,即会列出一些类型的随机试验所有可能出现的结果(基本事件),理解等可能的意义,会根据随机试验结果的客观对称性或均衡性判断试验结果是否具有等可能性;(2)过程与方法目标,即让学生经历探索试验结果具有等可能性的过程,通过具体情境理解等可能性,在学习中培养和发展随机观念,初步形成用随机观念观察和分析问题的意识;(3)情感、态度和价值观目标,即在活动中,激发学生"学数学"的兴趣,体会"做数学"的乐趣,发展"用数学"的意识与能力.这个目标定位如何呢?

从目标关系上看,选手A将教学目标确定为三个方面,貌似符合课程标准"三维目标"要求.然而,三维目标是什么?是整个课程的目标,具体到一节课,子目标之间相互交融,是一个有机整体,不能截然分割和标签化.如在经历活动过程中掌握知识技能、积累活动经验,在发展能力的同时渗透数学思想、感受数学文化.另外,教学目标还要与教学内容紧密结合,做到小切口、具体化、有侧重、可操作.

从教育理念上看,选手A的教学目标中使用了"让" "培养""激发"等祈使句,折射出教者潜意识里"教师中心"的思想.《义务教育数学课程标准》(2011年版)(以下简称"课标2011版")使用了如下行为动词:在知识技能目标方面使用了"会""能""了解""理解""掌握"等词,在过程方法目标方面使用了"经历""探索""获得""发展"等词,在情感、态度、价值观目标方面使用了"体验(会)" "感受""形成"等词,这些行为动词在教育理念上强化了学生的主体地位.

从数学本质上说,本节课要让学生意识到:等可能性是人为建构的数学模型,这种建构具有合理性和必要性.现实中不存在绝对的等可能性,实验结果与计算结果不可能完全一致,用统计结果说明概率意义、用概率说明现实可能性是一种假设就是这个道理.

基于此,本节课的教学目标可以确定为:(1)会列出一些类型的随机试验的所有可能结果,通过数学试验活动,探索、归纳、理解等可能性的概念,体会试验的公平性,初步形成"公正、公平"意识;(2)会根据随机试验的条件(对称性或均衡性)判断试验结果是否具有等可能性,能根据要求设计简单的随机试验,逐步学会理性分析随机试验发生的结果可能性大小;(3)感受随机观念,体验等可能性在生活中的应用.

二、如何使情境设计更具科学性

选手B在引导学生探究等可能性条件时,设计了一个用Flash模拟演示"气球升空"情境:画面上,气球缓缓升空,其中一只气球升得最高(录像截图如图1).然后让几位学生点击鼠标重复演示,接着教者提问:每次试验有多少种可能的结果?它们都是随机事件吗?每次试验有几个结果出现?每个结果出现是等可能的吗?学生作出了令教者满意的回答,其目的是说明"气球升空"试验符合等可能性的条件:(1)每次试验都是随机事件;(2)每次试验的结果是唯一的;(3)每种结果的机会是均等的(即具有均衡性、对称性),笔者认为这个情境处理有待商榷.科学性是判定数学教学的第一标准,即数学教学要符合自然现实、数学自身和认知规律的科学性.真实版"气球升空"情况如何呢?由于气球质地、形状、大小不尽完全相同,气球在升空前不一定处于同一高度,升空后最高处的气球也不一定唯一,所以"气球升空"试验不完全具备等可能性的随机、均衡和对称条件,用虚拟演示替代真实场景来说明等可能性条件不具有科学性.显然电脑软件演示"气球升空"试验是一种逻辑颠倒,是教者的人为设定、主观臆想和一厢情愿.

图1

三、如何突破教学难点

本节课的学习是为后面研究"等可能条件下的概率"作准备,求概率的前提条件就是"等可能出现的结果数",这是本节课教学的重点与难点,但这一点往往被教者忽视.这让笔者想到某学校2015-2016学年度九年级期中考试试题:一个不透明的盒子中装一些球(除了颜色外无其他差别),从中随机抽取一个小球,共有三种可能的情况:红球、黄球和绿球,则随机摸出一球是红球的概率为().

试题的得分率为0.48左右,大多数学生选择了"C",产生这种现象的原因何在?我们知道,一般地,如果一个实验有n个等可能的结果,当其中的m个结果之一出现时,事件A发生,那么事件A发生的概率P(A)=,使用这个计算公式的前提是"等可能出现的结果数",苏科版教材的例2为我们提供了突破难点的好素材,可惜不少教师在教学中忽视了对这个前提条件的强化.

(教材例2)一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出1只球,摸到白球与摸到红球是等可能的吗?为什么?

摸到的球不是白球就是红球,所以摸到白球与摸到红球是等可能的.

小明

摸到每一个球的可能性相同,而红球有2个,白球只有1个,摸到红球的可能性大.

小丽

这个例题的价值何在?教学中需要注意什么?从教学价值来说,一是强化对"等可能性条件"的理解,其中的关键词"不透明的袋子""任意摸"是进一步感受试验条件的均衡性,"球除颜色外都相同""搅匀"是加深对试验条件对称性的感悟;二是突破难点,即区别一次试验中"个体出现的所有可能的结果数"与"某一类现象发生的可能的结果数".教学中,将小球编号列出一次"摸球"的可能性结果有白、红1、红23种,而其中摸到白球的可能性是一种,摸到红球的可能性是红1、红2两种.通过试验、思考、讨论、点拨,学生认识到"摸球"试验中,一次摸到每个小球的可能性是相同的,所有等可能的结果数是3,而摸到某一种颜色的小球的可能性不同.某校的那道试题条件"一个不透明的盒子中装一些球",小球的总个数和红球的个数未知,所以无法确定一次"摸球"试验中所有可能的结果数,当然就不能求出"随机摸出一球是红球"的概率.

四、如何让数学活动指向数学思维

数学课堂是思维的课堂,"等可能性"教学也不例外,所有活动都应该围绕概念的生成、试验与模型的关系展开思维活动.然而不少选手却以炫丽的形式掩盖了数学的思维.下面是选手C在等可能性概念引入环节的教学实录.

问题情境:学校要从3名演讲比赛优秀者中挑选1名同学,代表学校去市文化馆参加颁奖仪式.确定人选的方法是:袋子中有红、黄、绿3只球,请甲、乙、丙3位优胜者摸球,摸到红球者作领奖代表.

活动一:在不透明塑料袋中有红、黄、绿3只球,其中红球较大.学生轰笑,教师像煞有介事继续搅匀请甲、乙、丙3位优胜者摸球,先摸球者理所当然摸出了红球.学生愤愤不平,认为这种方式不公平.师问:为什么不公平?生:因为球大小不一样,3只球必须"除了颜色外,其他都相同".

活动二:透明塑料袋中装有红、黄、绿3只球,除了颜色外,其他都相同,教师搅匀后请甲、乙、丙3位优胜者摸球.没等优胜者摸球,众学生"抗议",教者继续让学生乙摸球,结果可想而知.教师提问:大家为什么"抗议"?众生:因为袋子透明,先摸的人一定会摸出红球,仍然不公平.

活动三:红、黄、绿3只小球除颜色外其他都相同.教师依次将它们放进一个瘦长(无法搅匀)的不透明袋子中,依次让甲、乙、丙3位优胜者摸球,结果丙摸到了红球,甲、乙两位同学满脸不快,因为这个试验不是随机的:袋子瘦长,小球无法搅匀,第一个放进去的红球在袋子最底层,所以最后一个摸球者必然摸到红球.

笔者在想:选手C设计这些活动的目的何在?或许是引发学生认知愤悱,引导学生从反面充分感受等可能性的随机性、均衡性和对称性,设计意图明确,目标指向明显.然而,教者是否考虑过:活动中学生为什么会"轰笑"、"抗议"和"不快"?---其实,这里学生无须"摸球",从现场"道具"中就能"看出"结果,而教者让学生机械地去摸球显得毫无意义.这就产生两个问题:一是什么时候需要操作?二是操作是必须的吗?

什么时候需要操作?笔者以为,基于3个方面的需求.一是通过操作活动,发现、猜想结论,这是所有自然科学探究的第一步.二是通过操作活动,验证先行抽象与想象的结果,进而归纳或演绎.如研究一些动点、动态问题时,让学生先想象运动过程与结果,再用几何画板动态演示验证结论,最后推理、计算.三是通过操作活动,加深对知识的感悟与理解.如画反比例函数y=的图像时,先根据研究一次函数图像时的经验,由函数式的数量关系对图像作大致判断:x>0时y>0,x<0时y<0,说明图像只能在第一、三象限;x≠0、y≠0,说明图像与坐标轴无公共点;当x→∞时y→0,当y→∞时x→0,说明图像无限接近坐标轴……接着由学生操作,经历列表、描点、连线并细化取点、不断修改完善的过程,从而得到比较准确的图像.这里对函数中变量值的讨论,是引导学生初步感知数量特征,判断图像大致位置与趋势,为研究函数性质提供直观感知,避免取值与画图的盲目性.

操作是必须的吗?学生操作活动的设计要切合学生的年龄特征、认识基础,操作实验要有明确的目标指向,要带着问题、指向思维,不能停留在表象、为操作而操作层面.比如在选手D设计的活动中,学生在摸球之前已经感受到了等可能性条件,"摸球"活动就没有必要继续;如果学生还满脸狐疑,活动就继续进行,以强化对等可能性特征的体验和感悟.教者应观察学生的反应,把握教学节奏,及时进行调整.

五、如何以问题驱动数学思考

在引入等可能性概念时,大多数选手设计了抛硬币、摸牌、摸球等游戏活动.在每个试验活动中,教者依次提出问题:硬币两面是均匀的吗?这个试验是否是随机事件?可能出现的结果数是多少?每次试验出现的结果数是多少?每个可能的结果出现的机会均等吗?在学生试验和师生问答中,教者将活动结果列成表格(PPT截图如图2),最后归纳出等可能性的条件,整个教学过程看似无懈可击.笔者不禁要问:表格中的问题和栏目是自然生成的吗?学生会想到这些问题吗?

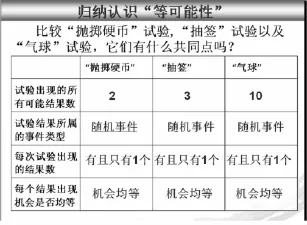
图2

课堂观察发现:教师通过学生试验活动,列出与可能性的条件相关的问题,设计好了所有需要思考与表述的内容,学生只要回答"是""不是""1个、2个……""均等",归纳结论时只要将黑板(或屏幕)上的文字连起来即可.所有问题由教者抛出,没有自然生成;所有结论是学生机械模仿,不是思考的结果.笔者还注意到,课堂上有学生在揣摩老师的意图:需要"我"如何配合让老师完成"表演",这是多么可怕的现象啊!

问题是数学的心脏,以问题驱动学生思考,实现教学目标达成,是行之有效的数学教学策略.课堂上问题从何而来?如何处理?笔者认为:课堂上的问题来源可分为置疑、质疑和悬疑三个方面(见《好家长.泰州教育》2015年第12期《基于四个"一三"的初中数学模拟课堂》),这三个方面逐层递进、层层深入,学生在生疑、质疑、释疑中建构知识、形成能力.

一是置疑.在学习的每个初始阶段,教师通过设问启发学生思考.如在等可能性教学伊始设计这样的情境:"将5个完全相同的球按照1-5编号放入一个不透明的袋子,搅匀后任意摸出一个球."教者提出如下问题: (1)任意摸出1球会有多少种结果?分别是什么?(2)一次实验会不会同时出现2个结果?(3)这5个球哪几号球可能先出现?哪个出现的次数多?教者不要急于让学生试验,而是让学生独立猜想与思考,然后将结论与同学交流分享,再做"摸球"试验,从而验证或否定自己的猜想,再归纳小结,达到建构概念的目的.

二是质疑.学生活动中生成问题,同伴合作思考.如选手D设计的"选取颁奖嘉宾"活动中,6名同学每人一只白球、6名同学每人一只黄球,将球放入不透明的袋子,从中抽取一个球,抽到白球,则白球持有者作为颁奖嘉宾.这时学生质疑:不一定抽出白球,即使抽出了白球,由于不知道球是几号同学的,就不能确定颁奖嘉宾.进而改进设计:将所有球分别编号为1-12再摸球就可以了.这样在引疑中质疑、在"无疑"处"生疑",达到深化理解概念的目的.

三是悬疑.学生学习反思产生新疑问,引发后续思考.如本节课小结反思环节,有学生提问:先摸后摸机会相同吗?这就是学生学习反思后生成的新问题,教者顺势引出新话题:"你提的问题很有价值,这正是我们下一节课将要研究的问题",达到激发学生渴求新知的目的.

六、如何处理好教师与学生的关系

选手D设计了"选幸运同学"的系列游戏,主要过程如下所示.(1)掷骰子(质地均匀的正方体).每位学生选定认为可能出现的数字,抛掷骰子一次,猜对的同学站立进入下一轮.(2)抛硬币(质地均匀).上一轮胜出的同学继续猜硬币抛后的正反,猜对的同学继续进入下一轮.(3)抽扑克牌(除数字外都相同).若上一轮胜出的同学不止一位,则继续通过抽扑克牌选取一名幸运学生. (4)抽颁奖词.若标有1、2、3的3张卡片背面分别写着不同的颁奖词,把它们放在一个盒子中,搅匀后从中任意抽出一张,被抽出编号卡片的背面内容就作为颁奖词. (5)从学号为1-12号的同学中选取一名学生为颁奖嘉宾……1-12号学生从白、黄两色乒乓球中选择一个……(6)读颁奖词,发大礼包.

在这个游戏中,那么多学生"被"摇号而站立座位许久,12名学生在讲台前排成一行"被"编号、"被"抽学号、"被"限定的范围逐步淘汰,最后剩下一位学生成为"大礼包"最终拥有者,而这位"幸运"学生脸上丝毫没有流露出胜利者的喜悦.看着那些配合"默契"、面无表情的学生,再看看发号施令、眉飞色舞的教师,学生从"课堂的主体"沦为"教师表演的道具",笔者有一种别样滋味涌心头.

"课标(2011版)"指出:"教学活动是师生积极参与、交往互动、共同发展的过程.有效的教学活动是学生学与教师教的统一,学生是学习的主体,教师是学习的组织者、引导者与合作者."问题是教师的组织者、引导者与合作者的角色怎么当?学生的主体地位如何体现?孙双金老师认为:"好的课堂是学生小脸通红、小眼发光、小手直举、小嘴常开",这是学生思维火花迸发的外在表现.课堂教学中,教者应该围绕教学目标,设计符合学生年龄与认知特点的活动,或让学生自主设计探索活动方案,通过自主探究、独立思考、小组交流和教师点拨,在经历活动过程中掌握知识技能,提升思维能力,积累活动经验,体会学习方法,达成教学目标.学生应当是充满生命张力与活力的"人",而不是教师主宰与摆布的对象;课堂应该成为学生兴趣盎然、个性发展的沃土,而不是教师表演的舞台.

七、如何体现良好的价值导向

在"感受等可能性条件"的教学环节,不少选手设计了给学生发奖品活动.有选手几次抛掷纪念硬币,让学生猜"正""反",谁猜中硬币就归谁;有选手让学生参加"比赛",获胜者奖励精美的大笔记本;还有选手以"幸运"抽奖的方式引入等可能性,用学生作"抽奖嘉宾",将"大礼包"送给最后被抽中的学生.这些活动折射出怎样的价值导向?

选手意在调动学生的学习兴趣和积极性,以实现"课标(2011版)"提出的情感、态度和价值观目标.问题是这种目标究竟以什么方式达成?笔者认为,情感、态度和价值观目标在这节课中应该体现为:学生在教师引导下经历有意义的数学活动过程,获得对数学的理解与领悟,增强数学学习的兴趣;学生自主思考、同伴互助,在克服思维障碍中获得解决数学问题的满足感,磨炼坚韧的意志;学生在感受数学的对称、简洁、奇异、抽象、理性之美中享受学习的快乐;学生接受数学文化的熏陶,从而对数学产生特殊的情感……反观我们的数学课堂,学生无需付出劳动,通过无谓的"猜"和"抽"就能获得物质回报,这种教育会把学生引向何方?在"大礼包"活动中,整节课把学生的注意力聚焦于"大礼包".不论礼包是真是假,其价值导向都与课程标准的要求相悖,也与九年级学生的心智特征不匹配.

教学中,我们主张在尊重教材的前提下,"积极开发利用社会教育资源",为学生"提供许多贴近时代、贴近生活的有意义话题……挖掘适合学生学习的素材……以增强学生学习数学的兴趣,提高学生运用数学解决问题的能力"(课标2011版).什么是"有意义的话题"?什么是"适合学生学习的素材"?笔者认为:所谓"有意义"与"适合",就是能够引发学生数学化思考、引导学生积极向上、磨炼学生坚韧意志、形成正确的价值观.比如我们引入"福利彩票抽奖"问题,应该让学生体会到:买彩票的目的不是为了得奖,根本动机是捐献,以微薄力量帮助他人.所买的彩票号是随机的,抽奖也是随机的,得奖那是一种"意外"(小概率事件),学生通过了解、研究"福利彩票抽奖"的规则,感受随机性和等可能性,这样才有良好的价值导向意义.